Занятие 8
Тригонометрические уравнения и неравенства.
Основные методы решений
Простейшие тригонометрические уравнения.
О. 1.1. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим.
К простейшим тригонометрическим уравнениям относятся уравнения:
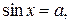



Рассмотрим их решения.
I. Уравнение 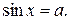
О. 1.2. Арксинусом числа а (обозначают arcsin a ), где  называется число t из отрезка
называется число t из отрезка  , синус которого равен а.
, синус которого равен а.
Итак, если  , то arcsin a = t:
, то arcsin a = t: 
Так как  то уравнение
то уравнение  имеет решение лишь в том случае, когда
имеет решение лишь в том случае, когда  . При выполнении этого условия все решения уравнения содержатся в формуле
. При выполнении этого условия все решения уравнения содержатся в формуле

Если же  , то уравнение I. не имеет действительных решений.
, то уравнение I. не имеет действительных решений.
Пример 1. Решить уравнение 

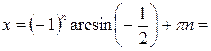


Пример 2. Решить уравнение 
Δ Это уравнение не имеет решений, так как √10>3и, значит, 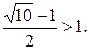
II. Уравнение 
О. 1.3. Арккосинусом числа а (обозначают arccos a), где  называется число t из отрезка
называется число t из отрезка  , косинус которого равен а.
, косинус которого равен а.
Итак, если  , то arccos a = t:
, то arccos a = t: 
Если  , то уравнение
, то уравнение  имеет решения
имеет решения 
Если  , то уравнение
, то уравнение  не имеет решений.
не имеет решений.
III. Уравнение 
О. 1.4. А рктангенсом числа а (обозначают arctga ) называется такое число t из интервала  , тангенс которого равен а.
, тангенс которого равен а.
Итак, arctg a = t: 
Уравнение  имеет решения
имеет решения 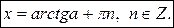
IV. Уравнение 
О. 1.5. А рккотангенсом числа а (обозначают arcсtga ) называется такое число t из интервала  котангенс которого равен а.
котангенс которого равен а.
Итак, arсctg a = t: 
Уравнение  имеет решения
имеет решения 
Для вычисления значений обратных тригонометрических функций справедливы формулы:

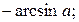



Пример 3. Решить уравнение 



Почленно разделив на 3, окончательно получаем: 
Пример 4. Решить уравнение 




Почленно умножая на 2, окончательно получаем: 
Замечание. Для решения уравнений 
 в случае, когда
в случае, когда 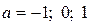 удобнее пользоваться более простыми соотношениями:
удобнее пользоваться более простыми соотношениями:
если  то
то 
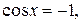 то
то 
если  то
то 
 то
то 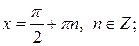
если  то
то 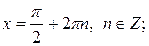
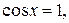 то
то 
Некоторые методы решения тригонометрических уравнений.
Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида и решение полученного простейшего тригонометрического уравнения (либо совокупности простейших тригонометрических уравнений). Рассмотрим основные методы сведения тригонометрических уравнений к простейшим тригонометрическим уравнениям.
Метод сведения к квадратному уравнению. Суть метода в том, что данное уравнение нужно преобразовать к такому виду, чтобы можно было обозначить через y какую либо тригонометрическую функцию или комбинацию таких функций. В результате получают квадратное уравнение относительно y, решая которое приходят либо к простейшему тригонометрическому уравнению, либо к более простому уравнению.
Пример 5. Решить уравнение 




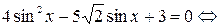
 так как
так как 


Пример 6. Решить уравнение 
Δ Заметим, что


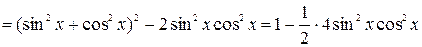

Подставим значение этого выражения в исходное уравнение:
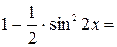





Метод группировки и разложения на множители.
Под разложением на множители будем понимать такое разложение, когда в правой части тригонометрического уравнения стоит число 0, а левая часть представлена в виде произведения нескольких сомножителей, содержащих тригонометрические выражения. После этого каждый из сомножителей приравнивается к нулю и затем решается совокупность более простых уравнений. Для разложения на множители могут быть применены известные формулы сокращённого умножения (см. Занятие 1), формулы суммы и разности тригонометрических функций (см. Занятие 7) и другие формулы.
Пример 6. Решить уравнение 
Δ 
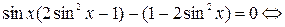


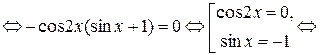



Метод приведения к однородному уравнению.
О. 2.1. Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла.
Например,  (1) - однородное уравнение 1-ой степени;
(1) - однородное уравнение 1-ой степени;
 (2) - однородное уравнение 2-ой степени, где А, В, С – некоторые числа.
(2) - однородное уравнение 2-ой степени, где А, В, С – некоторые числа.
Рассмотрим вначале решение уравнения (2). Пусть, например, 
Предположим, что  , тогда уравнение (2) примет вид:
, тогда уравнение (2) примет вид:
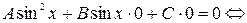

 чего не может быть, так как синус и косинус не могут одновременно равняться нулю, поскольку это противоречит основному тригонометрическому тождеству:
чего не может быть, так как синус и косинус не могут одновременно равняться нулю, поскольку это противоречит основному тригонометрическому тождеству: 
Значит, 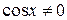 и можно почленно разделить уравнение (2) на
и можно почленно разделить уравнение (2) на 
Получим квадратное уравнение относительно тангенса 
К уравнению (2) сводятся уравнения вида:
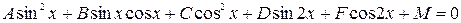
посредством формул синуса и косинуса двойного угла и представления числа 1 в виде  Точно так же, при помощи деления на
Точно так же, при помощи деления на 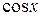 или
или  решается уравнение (1).
решается уравнение (1).
Пример 7. Решить уравнение 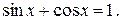
Δ Перенесём все члены уравнения влево, а затем преобразуем и разложим на множители выражение в левой части уравнения:


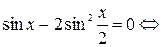
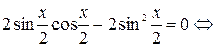

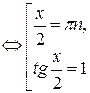
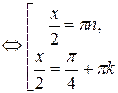

Заметим, что уравнение  совокупности является однородным уравнением 1-ой степени.
совокупности является однородным уравнением 1-ой степени.
Метод введения вспомогательного угла.
Рассмотрим уравнение вида: 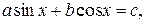 где a, b, c – числа (a, b
где a, b, c – числа (a, b  .
.
Разделим обе части этого уравнения на число 
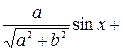


Теперь коэффициенты уравнения обладают свойствами синуса и косинуса, а именно: модуль каждого из них не больше 1, а сумма их квадратов равна 1. Тогда можно обозначить их соответственно, как  и
и 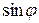 (здесь
(здесь  - так называемый вспомогательный угол), и уравнение (3) принимает вид:
- так называемый вспомогательный угол), и уравнение (3) принимает вид:

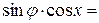
 или
или 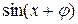
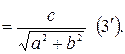
a) Если  то уравнение
то уравнение  , а значит и исходное уравнение не имеет решений.
, а значит и исходное уравнение не имеет решений.
б) Если  то уравнение
то уравнение  , а значит и исходное уравнение имеет решение:
, а значит и исходное уравнение имеет решение: 
где 
Пример 8. Решить уравнение 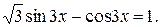
Δ Здесь  , поэтому делим обе части уравнения на
, поэтому делим обе части уравнения на 











