Вторая космическая скорость

Малые колебания

-kx⃗=ma⃗; a⃗=m ; ; x=ACos(ωt+α); x`= =-ASin(ωt+α)ω; x``= =-ACos(ωt+α)ω²; ω= ; ωT=2π; T= =2m ; период-минимальный интервал времени спустя который система возвращается в исходное положение; -частота; ωt+α-фаза; α-начальная фаза

Физический маятник. Математический маятник

Центр качения- точка которая лежит на прямой соединяющей точку подвеса и центра масс; Физический маятник —представляет собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела. ; - приведённая длина;

Математический маятник: ϕ≪1; в соответствии со 2 законом Ньютона; mg⃗+N⃗=ma⃗; y: -mg+N=0;N=mg; x: -NSinϕ=m ; ; x=ASin(ωt+α); x`= ACos(ωt+α)ω; x``= =-ASin(ωt+α)ω²;ω= ;T=2π

Затухающие колебания

Затухающие колебания — колебания, энергия которых уменьшается с течением времени.

Вынужденные колебания. Резонанс

Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени. В случае вынужденных колебаний устанавливается амплитуда колебаний, которая не связана с начальными условиями, а определяется свойствами колебательной системы, периодом и амплитудой колебаний внешней силы, а также энергетическими потерями, обусловленными силами трения (сопротивления). Когда период вынуждающей колебания внешней силы совпадает с собственным периодом колебаний данной колебательной системы, наступает резонанс.

Резона́нс— явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы.

Сложение колебаний. Векторная диаграмма

складываются гармонические колебания с одинаковой частотой, но разными амплитудами и начальными фазами: x 1 = x 1msin(ω t + ϕ1) и x 2 = x 2msin(ω t + ϕ2). Результирующее гармоническое колебание представим в виде X = X msin(ω t + Ф).

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов

Движение в центральном поле сил. Эффективная энергия

Кемплерова задача

Космические скорости

Первая космическая скорость

; V= = первая космическая скорость — это минимальная скорость, при которой тело, движущееся горизонтально над поверхностью планеты, не упадёт на неё, а будет двигаться по круговой орбите.

Вторая космическая скорость

; G 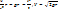=11 км/с Минимальная скорость, которую нужно сообщить телу на поверхности Земли, чтобы оно ее покинуло, двигаясь по незамкнутой траектории, называется второй космической скоростью. При такой начальной скорости тело преодолевает притяжение Земли и становится спутником Солнца

Преобразования Лоренца

; Из преобразований Лоренца следует очень важный вывод о том, что как рассто­яние, так и промежуток времени между двумя событиями меняются при переходе от одной инерциальной системы отсчета к другой, в то время как в рамках пре­образований Галилея эти величины счита­лись абсолютными, не изменяющимися при переходе от системы к системе. Кроме того, как пространственные, так и времен­ные преобразования не явля­ются независимыми, поскольку в закон преобразования координат входит время, а в закон преобразования времени — про­странственные координаты, т. е. устанав­ливается взаимосвязь пространства и вре­мени. Таким образом, теория Эйнштейна оперирует не с трехмерным простран­ством, к которому присоединяется понятие времени, а рассматривает неразрывно свя­занные пространственные и временные ко­ординаты, образующие четырехмерное пространство-время.

10.Длина тела в разных системах отчёта

длина стержня, измерен­ная в системе, относительно которой он движется, оказывается меньше длины, из­меренной в системе, относительно которой стержень покоится. Если стержень покоит­ся в системе К, то, определяя его длину в системе К', по формуле ;

11.Длительность событий в разных системах отчёта

; длительность события, проис­ходящего в некоторой точке, наименьшая в той инерциальной системе отсчета, отно­сительно которой эта точка неподвижна. Часы, движущиеся относительно инерциальной системы отсчета, идут медленнее покоя­щихся часов, т. е. ход часов замедляется в системе отсчета, относительно которой часы движутся. следует, что замедле­ние хода часов становится заметным лишь при скоростях, близких к скорости света в вакууме.

12.Одновременность событий в разных системах отчёта