Задача 1. Пусть имеется следующий временный ряд:

Известно также, что 
Определить для этого временного ряда значение коэффициента автокорреляции первого порядка.
Решение. Значение коэффициента определим по формуле:

Распишем все компоненты этой формулы. Числитель преобразуем следующим путем:

Здесь  значения средних вычисляем по соответствующим формулам; при этом значения сумм рассчитываются с учетом крайних значений временного ряда:
значения средних вычисляем по соответствующим формулам; при этом значения сумм рассчитываются с учетом крайних значений временного ряда:


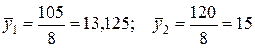
Отсюда:  +
+ 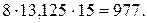
Аналогично рассчитываем каждый член в знаменателе:


Результат определим по исходной расчетной формуле:

Пример 2. На основе квартальных данных объемов продаж предприятия за 1995-2000 гг. была построена аддитивная модель временного ряда, трендовая компонента которой имеет вид:


Показатели за 1999 г. приведены в таблице:
| Квартал | Фактический объем продаж | Компонента аддитивной модели | ||
| трендовая | сезонная | случайная | ||
| -11 | ||||
Определить недостающие в таблице данные, учитывая что общий объем продаж за 1999 г. составил 1000 тыс. у.е.
Решение. В первую очередь определим все значения трендовой компоненты. Чтобы использовать имеющееся уравнение тренда, надо определить моменты времени, относящиеся к 1999 г. Поскольку модель относится к периоду 1995м – 2000 гг., т.е. охватывает 6 лет, квартальные временные отметки изменяются от 1 до 24. В этом случае 1999 г. (предпоследний в исследуемом периоде) соответствует моментам времени 17, 18, 19 и 20.
Подставим в уравнение тренда, получим:
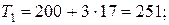



Далее недостающие величины для первого, второго и третьего кварталов вычисляем по балансу из уравнения для аддитивной модели временного ряда:



Осталось определить только величины для четвертого квартала, где известно только значение трендовой компоненты. В условиях задачи задан общий объем продаж за год. Поскольку известны продажи за три первых квартала, четвертый определяется легко:

Для расчета сезонной компоненты за 4 – й квартал воспользуемся тем, что в аддитивной модели сумма сезонных компонент за один период должны равняться нулю:

Последнее значение в таблице – случайную компоненту за 4 – й квартал – вычисляем по балансу из уравнения аддитивной модели, поскольку все остальные компоненты уже известны:

| Квартал | Фактический объем продаж | Компонента аддитивной модели | ||
| трендовая | сезонная | случайная | ||
| - 40 | -11 | |||
| - 39 | ||||
| - 7 |
Пример 3. На основе поквартальных данных за 9 последних лет была построена мультипликативная модель некоторого временного ряда. Уравнение тренда в этой модели имеет вид:
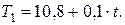
Скорректированные значения сезонной компоненты равны: в 1–м квартале – 1,5; в 3–м квартале – 0,6; в 4–м квартале – 0,8.
Определить сезонную компоненту за 2 – й квартал и прогноз моделируемого показателя за 2 – й и 3 – й кварталы следующего года.
Решение. В мультипликативной модели сумма скорректированных сезонных компонент за один период должны равняться количеству этих коэффициентов, т.е. четырем. Отсюда находим недостающую сезонную компоненту за 2–й квартал:

Для прогнозирования по мультипликативной модели воспользуемся соотношением (2), в котором не будем учитывать случайную компоненту. При этом следует иметь в виду, что 2–й и 3–й кварталы будущего года будут относиться в рамках рассматриваемой модели соответственно к 38–й и 39–й отметкам времени соответственно:


Пример 4. На основе помесячных данных за последние 5 лет была построена аддитивная временная модель потребления тепла в районе. Скорректированные значения сезонной компоненты приведены в таблице
| Январь | + 27 | Май | - 20 | Сентябрь | - 10 |
| Февраль | + 22 | Июнь | - 34 | Октябрь | + 12 |
| Март | + 15 | Июль | - 42 | Ноябрь | +20 |
| Апрель | - 2 | Август | - 18 | Декабрь | ? |
Уравнение тренда выглядит так:

Определить значение сезонной компоненты за декабрь, а также точечный прогноз потребления тепла на 2–й квартал следующего года.
Решение. В аддитивной модели временного ряда сумма скорректированных сезонных компонент за один период, в данном случае за год, должна равняться нулю. Отсюда значение сезонной компоненты за декабрь:

Прогноз потребления тепла рассчитывается по формуле для детерминированной составляющей ряда, в которой не учитывается случайная составляющая, поскольку она не прогнозируется. Здесь для расчета трендовой компоненты следует иметь в виду, что второму кварталу следующего года (апрель, май, июнь) соответствуют отметки времени 64, 65 и 66. Прогноз за весь второй квартал складывается из прогнозов за апрель, май и июнь.

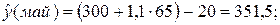

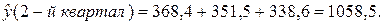
Пример 5.
Дана таблица:
| Момент времени | 
| 
| 
| 
| 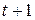
|

| |||||

| - |
где  ,
,  - ожидаемый и действительный объемы предложения. Определить значения
- ожидаемый и действительный объемы предложения. Определить значения  в соответствии с моделью адаптивных ожиданий, приняв
в соответствии с моделью адаптивных ожиданий, приняв 
Решение. Расчет ожидаемых значений проводим по формуле:
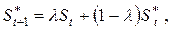
которая модифицируется для каждого момента времени 
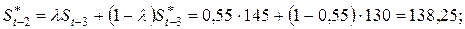

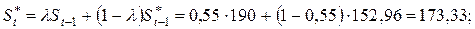

Желаю успехов!!!






