В 1
1)Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
РЕШЕНИЕ
1) На сколько человек всего рассчитан теплоход?
750+25 = 775
2) Сколько шлюпок необходимо, чтобы всех разместить?
775:70 = 11 шлюпок (остаток 5 человек)
Итак, в 11 шлюпок поместятся все люди, кроме 5 человек. Чтобы разместить и этих 5, нужна еще одна шлюпка. Итого будет нужно 12 шлюпок.
Ответ: 12 шлюпок.
2) Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?
Чтобы найти процент от числа, нужно число умножить на процент.
Под словами "умножить на процент" понимается, что если в задаче указано 25%, то умножать нужно на 0.25, а не на 25. Вообще, x процентов - это x разделить на 100:
x% = x:100,
25% = 25:100 = 0.25,
40% = 40:100 = 0,4 и т.д.
РЕШЕНИЕ
1) На сколько повысится цена шариковой ручки?
40 · (10%) = 40 · 0,1 = 4 (рубля)
2) Какова будет цена ручки?
40+4 = 44 (рубля)
3) Сколько ручек можно будет купить на 900 рублей? (Разделим 900 на 44 с остатком, чтобы узнать ответ):
900:44 = 20 ручек (остаток 20 рублей)
Смысл ответа в том, что мы сможем купить 20 ручек (частное), и у нас еще останется 20 рублей (остаток).
Ответ: 20 ручек.
3) Аня купила проездной билет на месяц и сделала за месяц 41 поездку. Сколько рублей она сэкономила, если проездной билет на месяц стоит 580 рублей, а разовая поездка — 20 рублей?
РЕШЕНИЕ
1) Сколько бы заплатила Аня за поездки, если бы не брала проездной?
41 · 20 = 820 (рублей)
2) Сколько Аня сэкономила?
820 - 580 = 240 (рублей)
Ответ: 240 рублей.
4) Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
РЕШЕНИЕ
1) Сколько граммов лекарства нужно выпить больному за весь курс лечения?
0,5 · 3 · 21 = 31,5 (г)
2) Сколько граммов лекарства находится в одной упаковке?
10 · 0,5 = 5 (г)
3) Сколько упаковок нужно больному (разделим 31,5 на 5 с остатком, чтобы узнать):
31,5:5 = 6 упаковок (остаток 1,5 г)
Смысл ответа в том, что если купить 6 упаковок, то не хватит 1,5 г. Чтобы хватило, нужно докупить еще одну упаковку. Итого 6+1=7 упаковок.
Ответ: 7 упаковок.
5) Шоколадка стоит 35 рублей. В воскресенье в супермаркете действует специальное предложение: заплатив за две шоколадки, покупатель получает три (одну в подарок). Сколько шоколадок можно получить на 200 рублей в воскресенье?
РЕШЕНИЕ
Две шоколадки стоят 70 рублей. Сначала будем покупать по 2 шоколадки (платить по 70 р), пока хватает денег, чтобы каждый раз получать третью. Потом, если хватит оставшихся денег, купим еще одну шоколадку уже за 35 р.
1) Сколько раз можно заплатить за две шоколадки и сколько денег после этого останется? (Разделим 200 на 70 с остатком, чтобы узнать):
200:70 = 2 раза (остаток 60 р)
2) Сколько шоколадок мы получим?
2 раза = 2 · 3 шоколадки = 6 шоколадок
60 р израсходуем на покупку еще 1 шоколадки, останется 60-35 = 25 р
Итого: 7 шоколадок и 25 р сдачи.
Ответ: 7 шоколадок.
_________________________________________________________________
6) Железнодорожный билет для взрослого стоит 720 рублей. Стоимость билета для школьника составляет 50% от стоимости билета для взрослого. Группа состоит из 15 школьников и 2 взрослых. Сколько рублей стоят билеты на всю группу?
РЕШЕНИЕ
1) Сколько стоит билет для школьника?
720 · (50%) = 720 · 0,5 = 360 (рублей)
2) Сколько стоят билеты на всю группу? (720 · 2 стоят билеты для взрослых, 15 · 360 стоят билеты для детей):
720 · 2+15 · 360 = 6840 (рублей)
Ответ: 6840 рублей.
7) Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
Как находить процент от числа. В этой задаче мы будем находить 16% от стоимости чайника.
РЕШЕНИЕ
Пусть начальная цена чайника была х.
Повышение цены в рублях составило х · (16%) = х · 0,16
Стоимость чайника после повышения составила х + х · 0,16. Но по условию задачи, эта стоимость равна 3480 рублей. Можно составить уравнение и решить его:
х + х · 0,16 = 3480
1,16 х = 3480
х = 3480:1,16
х = 3000
Итак, изначально чайник стоил 3000 рублей.
Ответ: 3000 р.
8) В городе N живет  жителей. Среди них
жителей. Среди них  % детей и подростков. Среди взрослых жителей
% детей и подростков. Среди взрослых жителей  % не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?
% не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?
РЕШЕНИЕ
1) Сколько детей и подростков живет в городе? (Обратите внимание: 15% находим от населения всего города)
200 000 · (15%) = 200 000 · 0,15 = 30 000
2) Сколько в городе взрослого населения?
200 000 - 30 000 = 170 000
3) Сколько взрослых жителей не работает? (Обратите внимание: 45% находим от взрослого населения)
170 000 · (45%) = 170 000 · 0,45 = 76 500
4) Сколько взрослых жителей работает?
170 000 - 76 500 = 93 500
Ответ: 93 500 жителей города работают.
9) Налог на доходы составляет  от заработной платы. После удержания налога на доходы Мария Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
от заработной платы. После удержания налога на доходы Мария Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марии Константиновны?
РЕШЕНИЕ
Пусть начальная зарплата Марии Константиновны составляла х рублей.
Тогда вычет из этой зарплаты равен х · (13%) = х · 0,13
Значит, Мария Константиновна получила х - х · 0,13 рублей. Но эта сумма по условию равна 9570 рублей. Составим уравнение и решим его:
х - х · 0,13 = 9570
0,87 х = 9570
х = 9570:0,87
х = 11 000
Итак, Мария Константиновна получает 11 000 рублей.
Ответ: 11 000 рублей.
10) Павел Иванович купил американский автомобиль, спидометр которого показывает скорость в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 65 миль в час? Ответ округлите до целого числа.
РЕШЕНИЕ
В условии сказано, что американская миля равна 1609 м, то есть 1,609 км.
65 миль = 65 · 1,609 км = 104,58 км.
Значит, 65 миль/ч = 104,58 км/ч.
По правилам округления, 104,58 приближенно равно 105, если округлять до целых.
Ответ: 105 км/ч.
11) 1 киловатт-час электроэнергии стоит 1 рубль 80 копеек. Счетчик электроэнергии 1 ноября показывал 12625 киловатт-часов, а 1 декабря показывал 12802 киловатт-часа. Сколько рублей нужно заплатить за электроэнергию за ноябрь?
РЕШЕНИЕ
1) Сколько израсходовано электроэнергии?
12 802 - 12 625 = 177 (кВт · ч)
2) Сколько нужно заплатить за всю электроэнергию?
177 · 1,8 = 318,6 (рублей), или 318 рублей 60 копеек.
Ответ: 318,6 рублей.
| , |
12) Поезд Новосибирск-Красноярск отправляется в  , а прибывает в
, а прибывает в  на следующий день (время московское). Сколько часов поезд находится в пути?
на следующий день (время московское). Сколько часов поезд находится в пути?
РЕШЕНИЕ
Если бы поезд отправлялся в 16:20, и прибывал бы в 4:20, то он был бы в пути 12 ч (половина суток). Но поскольку он отправляется на час раньше, в 15:20, то в пути он пробудет 12+1 = 13 ч.
Ответ: 13 часов.
13) а сливочного масла стоит 60 рублей. Пенсионерам магазин делает скидку 5%. Сколько рублей заплатит пенсионер за пачку масла?
РЕШЕНИЕ
1) Сколько составит скидка пенсионеру?
60 · (5%) = 60 · 0,05 = 3 (рубля)
2) Сколько заплатит пенсионер за пачку масла?
60 - 3 = 57 (рублей)
Ответ: 57 рублей.
В 2
1) На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какая была температура 15 июля. Ответ дайте в градусах Цельсия.

РЕШЕНИЕ
1) Находим на оси ОХ (горизонталь) точку "15" и мысленно восставляем перпендикуляр вверх, пока не "наткнемся" на график. Запоминаем точку на графике, на которую "наткнулись".
2) Из этой точки на графике опускаем перпендикуляр на ось OY. Попадаем в точку 19.
Итак, 15 июля температура воздуха была 19 градусов по Цельсию.
Ответ: 19
2) Когда самолет находится в горизонтальном полете, подъемная сила, действующая на крылья, зависит только от скорости. На рисунке изображена эта зависимость для некоторого самолета. На оси абсцисс откладывается скорость (в километрах в час), на оси ординат – сила (в тоннах силы). Определите по рисунку, чему равна подъемная сила (в тоннах силы) при скорости 200 км/ч?

РЕШЕНИЕ
1) Находим на оси OX (горизонтальной) точку, соответствующую скорости 200 км/ч. Она на графике не отмечена, но есть точка, соответствующая 100 км/ч. Если 100 км/ч - одна клеточка, то 200 км/ч - две клеточки вправо от 0 по оси OX.
2) Из точки "200 км/ч" по оси ОХ мысленно проводим вверх перпендикуляр, пока не "наткнемся" на график. Запоминаем точку, на которую "наткнулись".
3) Из этой точки на графике опускаем перпендикуляр на ось OY. Попадаем в точку 1.
Итак, при скорости 200 км/ч сила равна 1 тс.
Ответ: 1
3) На графике изображена зависимость крутящего момента двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту, на оси ординат — крутящий момент в Н  м. Скорость автомобиля (в км/ч) приближенно выражается формулой
м. Скорость автомобиля (в км/ч) приближенно выражается формулой  , где
, где  — число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н
— число оборотов двигателя в минуту. С какой наименьшей скоростью должен двигаться автомобиль, чтобы крутящий момент был не меньше 120 Н  м? Ответ дайте в километрах в час.
м? Ответ дайте в километрах в час.

РЕШЕНИЕ
1) Находим на оси OY (вертикальной) точку "120 Н · м". Мысленно проводим перпендикуляр из этой точки к оси OY (этот перпендикуляр будет попросту горизонтальной линией), пока не "наткнемся" на график. Запоминаем точку, на которую "наткнулись".
2) Из этой точки на графике опускаем перпендикуляр на ось OX. Попадаем в точку "2000 об/мин".
Значит, наименьшее число оборотов в минуту, удовлетворяющее условию задачи - это 2000.
3) Теперь по формуле v = 0,036 n найдем скорость:
v = 0,036 · 2000 = 72 (км/ч)
Ответ: 72
P.S. То, что точке "120 Н · м" соответствует еще и точка "5000 об/мин", на решение никак не повлияет. Нас ведь интересует наименьшая скорость, а значит, наименьшее число оборотов, то есть 2000 об/мин.
4) На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.
 РЕШЕНИЕ
РЕШЕНИЕ
Поскольку среднемесячная температура откладывается по оси OY, то наименьшая температура соответствует самому "низкому" столбику на диаграмме.
Самый низкий столбик второй по счету (вроде как февраль). Средняя температура в этот месяц была равна минус четырнадцати градусам (-14). Ответ: -14
5) На диаграмме показано количество посетителей сайта РИА Новости во все дни с 10 по 29 ноября 2009 года. По горизонтали указываются дни месяца, по вертикали — количество посетителей сайта за данный день. Определите по диаграмме, во сколько раз наибольшее количество посетителей больше, чем наименьшее количество посетителей за день.

РЕШЕНИЕ
Наибольшее число посетителей соответствут самому высокому столбцу диаграммы (например, 12 ноября). Количество посетителей 800 000.
Наименьшее число посетителей соответствут самому низкому столбцу диаграммы (15 ноября). Количество посетителей 400 000.
Наибольшее 800 000 разделим на наименьшее 400 000 и получим2:
800 000: 400 000 = 2
Итак, наибольшее число посетителей больше наименьшего в два раза.
Ответ: 2
6) На рисунке жирными точками показано суточное количество осадков, выпадавших в Томске с 8 по 24 января 2005 года. По горизонтали указываются числа месяца, по вертикали — количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку, сколько дней выпадало более 2 миллиметров осадков.

РЕШЕНИЕ
Более двух миллиметров выпадало в те дни, точки которых лежат выше горизонтальной линии, проведенной из точки "2,0" по оси OY. Это точки графика, соответствующие числам 8, 12, 14 января - всего 3 точки.
Ответ: 3
В 3 Формула Пика n – число целочисленных точек внутри многоугольника;
m - число целочисленных точек на границе многоугольника;
s – площадь многоугольника, ед.2.
Площадь вычисляется по формуле Пика:

1)  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Решение.
Площадь прямоугольного треугольника равна половине произведения его катетов. Поэтому
 см2.
см2.
Ответ: 6.
2) На клетчатой бумаге с клетками размером 1 см  1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах.
Решение.
 Площадь треугольника равна разности площади прямоугольника и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
Площадь треугольника равна разности площади прямоугольника и трех прямоугольных треугольников, гипотенузы которых являются сторонами исходного треугольника. Поэтому
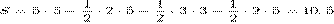 см2.
см2.
Ответ: 10,5.
3)  На клетчатой бумаге с клетками размером 1 см
На клетчатой бумаге с клетками размером 1 см  1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
Решение.
Площадь трапеции равна произведению полусуммы оснований на высоту. Поэтому
 см2. Ответ: 32,5.
см2. Ответ: 32,5.
В 4 1) Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?
| Перевозчик | Стоимость перевозки одним автомобилем (руб. на 100 км) | Грузоподъемность автомобилей (тонн) |
| А | 3,5 | |
| Б | ||
| В |
Решение.
Для перевозки 45 тонн груза перевозчику A понадобится 13 автомобилей. Стоимость перевозки каждым из них составит 32  1300 = 41 600 руб. Полная стоимость перевозки 41 600
1300 = 41 600 руб. Полная стоимость перевозки 41 600  13 = 540 800 руб.
13 = 540 800 руб.
Для перевозки 45 тонн груза перевозчику Б понадобится 9 автомобилей. Стоимость перевозки каждым из них составит 1  1300 = 53 300 руб. Полная стоимость перевозки 53 300
1300 = 53 300 руб. Полная стоимость перевозки 53 300  9 = 479 700 руб.
9 = 479 700 руб.
Для перевозки 45 тонн груза перевозчику В понадобится 4 автомобиля. Стоимость перевозки каждым из них составит 95  1300 = 123 500 руб. полная стоимость перевозки 123 500
1300 = 123 500 руб. полная стоимость перевозки 123 500  4 = 494 000 руб.
4 = 494 000 руб.
Стоимость самой дешевой перевозки составит 479 700 руб.
Ответ: 479 700.
2) Для изготовления книжных полок требуется заказать 48 одинаковых стекол в одной из трех фирм. Площадь каждого стекла 0,25  . В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей будет стоить самый дешевый заказ?
. В таблице приведены цены на стекло, а также на резку стекол и шлифовку края. Сколько рублей будет стоить самый дешевый заказ?
| Фирма | Цена стекла (руб. за 1 м2) | Резка и шлифовка (руб. за одно стекло) |
| A | ||
| Б | ||
| В |
Решение.
Общая площадь стекла, которого нужно изготовить, равна 48  0,25 = 12
0,25 = 12  . Рассмотрим различные варианты.
. Рассмотрим различные варианты.
Стоимость заказа в фирме А складывается из стоимости стекла 420  12 = 5040 руб. и стоимости его резки и шлифовки 75
12 = 5040 руб. и стоимости его резки и шлифовки 75  48 = 3600 руб. и равна 8640 руб.
48 = 3600 руб. и равна 8640 руб.
Стоимость заказа в фирме Б складывается из стоимости стекла 440  12=5280 руб. и стоимости его резки и шлифовки 65
12=5280 руб. и стоимости его резки и шлифовки 65  48 = 3120 руб. и равна 8400 руб.
48 = 3120 руб. и равна 8400 руб.
Стоимость заказа в фирме В складывается из стоимости стекла 470  12 = 5640 руб. и стоимости его резки и шлифовки 55
12 = 5640 руб. и стоимости его резки и шлифовки 55  48 = 2640 руб. и равна 8280 руб.
48 = 2640 руб. и равна 8280 руб.
Ответ: 8280.
3) Семья из трех человек едет из Санкт-Петербурга в Вологду. Можно ехать поездом, а можно — на своей машине. Билет на поезд на одного человека стоит 660 рублей. Автомобиль расходует 8 литров бензина на 100 километров пути, расстояние по шоссе равно 700 км, а цена бензина равна 19,5 рублей за литр. Сколько рублей придется заплатить за наиболее дешевую поездку на троих?
Решение.
Стоимость поездки на поезде для троих человек будет составлять 660  3 = 1980 руб. Расход бензина на 700 км пути составит 7 раз по 8 литров т. е. 56 литров. Его стоимость 56
3 = 1980 руб. Расход бензина на 700 км пути составит 7 раз по 8 литров т. е. 56 литров. Его стоимость 56  19,5 = 1092 руб.
19,5 = 1092 руб.
Ответ: 1092.
4) Строительной фирме нужно приобрести 75 кубометров пенобетона у одного из трех поставщиков. Цены и условия доставки приведены в таблице. Сколько рублей придется заплатить за самую дешевую покупку с доставкой?
| Поставщик | Стоимость пенобетона (руб. за за 1 м3) | Стоимость доставки | Дополнительные условия |
| A | 4500 руб. | ||
| Б | 5500 руб. | При заказе на сумму больше 150 000 руб. доставка бесплатно | |
| В | 3500 руб. | При заказе более 80 м3 доставка бесплатно |
Решение.
Рассмотрим различные варианты.
При покупке пенобетога у поставщика A стоимость заказа складывается из стоимости самого пенобетона 2 650  75 = 198 750 руб. и стоимости доставки. Всего 198 750 + 4 500 = 203 250 руб.
75 = 198 750 руб. и стоимости доставки. Всего 198 750 + 4 500 = 203 250 руб.
При покупке пенобетона у поставщика Б стоимость заказа складывается из стоимости самого пенобетона 2 700  75 = 202 500 руб. и стоимости его доставки. Но так как стоимость заказа больше 150 000 руб., то доставка бесплатно. Таким образом, стоимость заказа 202 500 руб.
75 = 202 500 руб. и стоимости его доставки. Но так как стоимость заказа больше 150 000 руб., то доставка бесплатно. Таким образом, стоимость заказа 202 500 руб.
При покупке пенобетона у поставщика В стоимость заказа складывается из стоимости самого пенобетона 2 680  75 = 201 000 руб. и стоимости доставки. Всего 201 000 + 3 500 = 204 500 руб.
75 = 201 000 руб. и стоимости доставки. Всего 201 000 + 3 500 = 204 500 руб.
Ответ: 202 500.
5) Для того, чтобы связать свитер, хозяйке нужно 400 граммов шерсти синего цвета. Можно купить синюю пряжу по цене 60 рублей за 50 г, а можно купить неокрашенную пряжу по цене 50 рублей за 50 г и окрасить ее. Один пакетик краски стоит 10 рублей и рассчитан на окраску 200 г пряжи. Какой вариант покупки дешевле? В ответ напишите, сколько рублей будет стоить эта покупка.
Решение.
Один моток пряжи весит 50 г., а на свитер нужно 8 мотков. Рассмотрим различные варианты.
Если покупать готовую пряжу синего цвета, то стоимость свитера будет 60  8 = 480 руб.
8 = 480 руб.
На неокрашенную пряжу нужно потратить 50  8 = 400 руб. Но на окраску пряжи потребуется 2 пакетика по 10 руб., то есть еще 20 руб. Итого на свитер из самостоятельно окрашенной пряжи потратится 420 руб.
8 = 400 руб. Но на окраску пряжи потребуется 2 пакетика по 10 руб., то есть еще 20 руб. Итого на свитер из самостоятельно окрашенной пряжи потратится 420 руб.
Ответ: 420.
В5 1)  . Избавляемся от логарифма по вышеприведенной схеме:
. Избавляемся от логарифма по вышеприведенной схеме:
27 = 4 - x,
4 - x = 128,
х = 4 - 128,
х = -124
Проверка. log2(4 - (-124)) = log2 128 = 7.
Ответ: -124.
2) Найдите корень уравнения  .
.
РЕШЕНИЕ
 . Избавляемся от логарифма по вышеприведенной схеме:
. Избавляемся от логарифма по вышеприведенной схеме:
15 + х = 3
х = 3 - 15
х = -12
Проверка. log2(15 + (-12)) = log23; log23 = log23
Ответ: -12
3) Найдите корень уравнения  .
.
1) Если аx = ay, то х = y.
2) 26 = 64.
РЕШЕНИЕ
 . Представим 64 как 26:
. Представим 64 как 26:
24-2 х = 26
4 - 2 х = 6
-2 х = 6 - 4
х = -1
Ответ: -1.
4) Найдите корень уравнения  .
.
1) Если аx = ay, то х = y.
2) 5-3 =  .
.
РЕШЕНИЕ
 . Представим
. Представим  как 5-3:
как 5-3:
5 х -7 = 5-3:
х - 7 = -3
х = -3+7
х = 4
Ответ: 4
5) Найдите корень уравнения  .
.
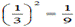 .
.
РЕШЕНИЕ
 . Представим 1/9 как (1/3)2:
. Представим 1/9 как (1/3)2:
(1/3) х - 8 = (1/3)2
х - 8 = 2
х = 2+8
х = 10
Ответ: 10
6) Найдите корень уравнения  .
.
РЕШЕНИЕ
 . Возведем обе части уравнения в квадрат и решим получившееся уравнение:
. Возведем обе части уравнения в квадрат и решим получившееся уравнение:

Ответ: 3.
7) Найдите корень уравнения 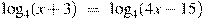 .
.
РЕШЕНИЕ
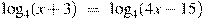
х + 3 = 4 х - 15;
3 х = 18;
х = 18:3;
х = 6
Проверка. log4(6+3) = log4(4 · 6 - 15); log49 = log49.
Ответ: 6
8) Найдите корень уравнения:  .
.
РЕШЕНИЕ
 . Это по сути пропорция. Перемножим ее крайние и средние члены и приравняем:
. Это по сути пропорция. Перемножим ее крайние и средние члены и приравняем:
9 х - 7 = 2;
9 х = 9;
х = 1.
Ответ: 1
9) Решите уравнение 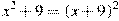 .
.
Формулу квадрата суммы.
РЕШЕНИЕ
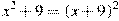 . Разложим правую часть по формуле квадрата суммы и решим получившееся уравнение:
. Разложим правую часть по формуле квадрата суммы и решим получившееся уравнение:
х 2+9 = х 2+18 х +81
18 х = -72
х = -4
Ответ: -4
10) Решите уравнение 
РЕШЕНИЕ
 . Разложив по формуле квадрата суммы левую часть, и по формуле квадрата разности правую, получим:
. Разложив по формуле квадрата суммы левую часть, и по формуле квадрата разности правую, получим:
4 х 2+28 х +49 = 4 х 2 - 4 х +1;
32 х = -48;
х = -48:32
х = -1,5
Ответ: -1,5.
11) Решите уравнение  . Если уравнение имеет более одного корня, в ответе запишите больший из корней.
. Если уравнение имеет более одного корня, в ответе запишите больший из корней.
РЕШЕНИЕ
 . По сути, это пропорция. Произведение крайних членов (х +8)(7 х +5) равно произведению ее средних членов (5 х +7)(х +8):
. По сути, это пропорция. Произведение крайних членов (х +8)(7 х +5) равно произведению ее средних членов (5 х +7)(х +8):
(х +8)(7 х +5) = (5 х +7)(х +8)
7 х 2+56 х +5 х +40 = 5 х 2+7 х +40 х +56
2 х 2+14 х - 16 = 0
х 2+7 х - 8 = 0
Можно решать это уравнение традиционным способом, вычисляя дискриминант, а затем корни. х 1 = -8, х 2 = 1.
Ответ: 1
12) Решите уравнение  . В ответе напишите наименьший положительный корень.
. В ответе напишите наименьший положительный корень.
РЕШЕНИЕ

Ответ: 0,5
13) Решите уравнение  .
.
Свойство степени дроби:

РЕШЕНИЕ

Ответ: -2
14) Решите уравнение  .
.
1) Если log ab = log aс, то b = с при a >0, b >0, c >0.
2) log aa = 1.
3) Сумма логарифмов равна логарифму произведения:
log ab +log ac = log a (b · c)
РЕШЕНИЕ
 . Представим 1 как log55:
. Представим 1 как log55:
log5(7 - х) = log5(3 - х) + log55
В правой части стоит сумма логарифмов. Представим ее как логарифм произведения и решим уравнение:
log5(7 - х) = log5((3 - х) · 5)
7 - х = 5(3 - х)
7 - х = 15 - 5 х
4 х = 8
х = 2
Проверка. log5(7 - 2) = log5(3 - 2) + 1; log55 = log51 + 1; 1 = 0 + 1; 1=1.
Ответ: 2
15) Решите уравнение  . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
. Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Если log ab = c, то аc = b. Это можно представить в виде следующей схемы 
При решении логарифмических уравнений обязательно делать проверку или проверять корни на принадлежность к области определения!
РЕШЕНИЕ
 . По вышеприведенной схеме имеем:
. По вышеприведенной схеме имеем:
(х - 5)2 = 49, откуда
х - 5 = 7 или х - 5 = -7
Решая эти два уравнения, имеем х 1 = 12 и х 2 = -2.
Проверка.
х 1 = 12: log12-549 = 2; log749 = 2; 2=2.
х 2 = -2: log-2-549 = 2; log-749 = 2; корень не подходит, поскольку основание логарифма не может быть отрицательным.
Итак, уравнение имеет единственный корень 12.
Ответ: 12.
16)Найдите корень уравнения: 
В ответе запишите наибольший отрицательный корень.
Формула корней уравнения cos x = a

РЕШЕНИЕ
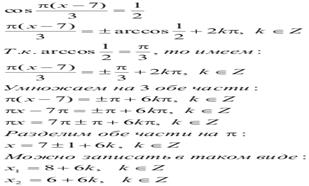 В ответ просят записать наибольший отрицательный корень. Нетрудно способом подбора догадаться, что для получения наибольшего отрицательного корня k нужно взять -2 и подставить в х 1:
В ответ просят записать наибольший отрицательный корень. Нетрудно способом подбора догадаться, что для получения наибольшего отрицательного корня k нужно взять -2 и подставить в х 1:
х 1 = 8+6 · (-2) = 8 - 12 = -4; -4 - это и есть наибольший отрицательный корень. Ответ: -4
В 6 
1) Найдите центральный угол  , если он на
, если он на  больше вписанного угла
больше вписанного угла  , опирающегося на ту же дугу. Ответ дайте в градусах.
, опирающегося на ту же дугу. Ответ дайте в градусах.
Свойство центральных и вписанных углов: вписанный угол равен половине соответствующего центрального угла.
РЕШЕНИЕ
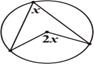
Воспользуемся тем, что вписанный угол равен половине соответствующего центрального угла. Пусть вписанный угол равен х, тогда соответствующий центральный угол будет 2 х. Но поскольку по условию центральный угол на 15о больше, то можем составить уравнение
2 х - х = 15,
откуда х = 15.
х - это вписанный угол, а соответствующий центральный равен 2 х = 2 · 15 = 30о
Ответ: 30
2) В треугольнике ABC угол C равен  ,
,  . Найдите
. Найдите  . Воспользуемся основным тригонометрическим тождеством для нахождения косинуса угла. Затем разделим синус на косинус и получим тангенс:
. Воспользуемся основным тригонометрическим тождеством для нахождения косинуса угла. Затем разделим синус на косинус и получим тангенс:

Ответ: 0,25
3) В треугольнике ABC угол C равен  ,
,  . Найдите
. Найдите  Чтобы найти синус угла В, достаточно найти косинус угла А. sin B = cos A. Находим по основному тригонометрическому тождеству cos A:
Чтобы найти синус угла В, достаточно найти косинус угла А. sin B = cos A. Находим по основному тригонометрическому тождеству cos A:
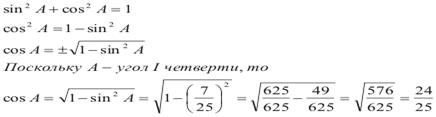
24:25 = 0,96.
Ответ: 0,96
4) В треугольнике ABC угол C равен  ,
,  . Найдите
. Найдите  . Чтобы найти косинус угла В, достаточно знать синус угла А. cos В = sin A = 0,1 по свойству дополнительных углов.
. Чтобы найти косинус угла В, достаточно знать синус угла А. cos В = sin A = 0,1 по свойству дополнительных углов.
Ответ: 0,1
5) В треугольнике ABC угол C равен  ,
,  ,
, 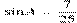 . Найдите AC. Катет АС, прилежащий к углу А, равен произведению гипотенузы АВ на косинус угла А. Гипотенуза у нас есть (АВ = 5), а косинус угла А (к которому прилежит искомый катет АС) неизвестен.
. Найдите AC. Катет АС, прилежащий к углу А, равен произведению гипотенузы АВ на косинус угла А. Гипотенуза у нас есть (АВ = 5), а косинус угла А (к которому прилежит искомый катет АС) неизвестен.
Воспользуемся основным тригонометрическим тождеством для нахождения косинуса угла:

24:25 = 0,96.
АС = АВ ·cos A = 5·0,96 = 4,8.
Ответ: 4,8
6) В треугольнике ABC угол C равен  , CH — высота,
, CH — высота,  ,
,  . Найдите AH. Из прямоугольного треугольника ACH: Катет (АН), прилежащий углу (А), равен произведению гипотенузы (АС) на косинус угла (А):
. Найдите AH. Из прямоугольного треугольника ACH: Катет (АН), прилежащий углу (А), равен произведению гипотенузы (АС) на косинус угла (А):
АН = АС · cos A (*)
Из прямоугольного треугольника ABC: Катет (АC), прилежащий углу (А), равен произведению гипотенузы (АB) на косинус угла (А):
АC = АB · cos A (**)
Подставим выражение (**) в (*):
АН = АС · cos A = (АB · cos A) · cos A = АВ · cos2 A.
Из основного тригонометрического тождества найдем cos2 A, затем, умножив на АВ, найдем АН:

Ответ: 15
7) В треугольнике ABC угол C равен  ,
,  ,
, 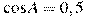 . Найдите высоту CH. Из треугольника ВСН: катет СН, прилежащий углу ВСН (углы ВСН и А равны) равен произведению гипотенузы ВС на косинус угла ВСН (то есть, на cos A):
. Найдите высоту CH. Из треугольника ВСН: катет СН, прилежащий углу ВСН (углы ВСН и А равны) равен произведению гипотенузы ВС на косинус угла ВСН (то есть, на cos A):
CH = BC · cos A = 8 · 0,5 = 4
Ответ: 4
8) В треугольнике ABC угол C равен  , CH — высота,
, CH — высота, 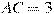 ,
,  . Найдите BH. Из основного тригонометрического тождества найдем косинус угла А:
. Найдите BH. Из основного тригонометрического тождества найдем косинус угла А:

Из треугольника АСН: катет АН, прилежащий углу А, равен произведению гипотенузы АС на косинус угла А:

Из треугольника АВС: катет АС, прилежащий углу А, равен произведению гипотенузы АВ на косинус угла А:

ВН = АВ - АН = 18 - 0,5 = 17,5
Ответ: 17,5
9) В треугольнике ABC  ,
,  ,
, 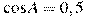 . Найдите AC.
. Найдите AC.

1) cos 60o = 0,5 (если это знать, решение сильно упростится, см. P.S.)
2) В равнобедренном треугольнике высота (СН на рисунке) является биссектрисой и медианой.
РЕШЕНИЕ
Рисунок к задаче см. на карточке-подсказке выше.
СН - высота равнобедренного треугольника, она же является и медианой, т.е. делит сторону АВ пополам, поэтому
АН = АВ: 2 = 8: 2 = 4
Из треугольника АСН: катет АН, прилежащий к углу А, равен произведению гипотенузы АС на косинус угла А:
АН = АС · cos A; откуда АС = АН: cos A = 4: 0,5 = 8
Ответ: 8 P.S. Можно было рассуждать и по-другому, если знать, что cos 60o = 0,5. В задаче сказано, что  , а значит, А = 60o. Т.к. в равнобедренном треугольнике углы при основании равны, то и В = 60o. Но поскольку сумма углов треугольника равна 180o, то третий угол треугольника С тоже равен 60o, а значит, треугольник равносторонний и АC = АB = ВС = 8.
, а значит, А = 60o. Т.к. в равнобедренном треугольнике углы при основании равны, то и В = 60o. Но поскольку сумма углов треугольника равна 180o, то третий угол треугольника С тоже равен 60o, а значит, треугольник равносторонний и АC = АB = ВС = 8.
10) В треугольнике ABC  ,
,  ,
, 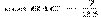 . Найдите высоту AH.
. Найдите высоту AH.

1) В равнобедренном треугольнике углы при основании равны (в нашей задаче это углы В и ВАС).
2) Основное тригонометрическое тождество sin2 A + cos2 A = 1.
3) У острых углов и синусы, и косинусы положительные.
4) Катет, противолежащий углу, равен произведению гипотенузы на синус угла.
РЕШЕНИЕ
Рисунок к задаче см. на карточке-подсказке выше.
1) Найдем синус угла ВАС по известному косинусу из основного тригонометрического тождества:

2) Из треугольника АВН: катет АН, противолежащий углу В, равен произведению гипотенузы АВ на синус угла В:
ВН = АВ · sin B, но т.к. углы В и ВАС равны, то
ВН = АВ · sin BАС = 5 · 0,96 = 4,8
Ответ: 4,8
11) В тупоугольном треугольнике ABC  , AH — высота,
, AH — высота,  . Найдите
. Найдите  .
.

1) Некоторые формулы приведения:
sin (90o+ x) = cos x cos (90o+ x) = - sin x tg (90o+ x) = -ctg x ctg (90o+ x) = - tg x
2) Котангенс угла - это отношение прилежащего катета к противолежащему.
3) У тупых углов синусы положительные, косинусы, тангенсы и котангенсы отрицательные
РЕШЕНИЕ
Рисунок к задаче см. на карточке-подсказке выше.
1) Найдем АН из треугольника АСН по теореме Пифагора:

2) АСВ = 90o+ САН (см. карточку-подсказку), поэтому tg ACB = -ctg CAH. Из треугольника САН: котангенс угла САН - это отношение прилежащего катета АН к противолежащему СН:
tg ACB = -ctg CAH = - АН: СН = -1: 4 = -0,25
Ответ: -0,25
12) Основания равнобедренной трапеции равны 17 и 87. Высота трапеции равна 14. Найдите тангенс острого угла.
РЕШЕНИЕ

По условию задачи, AB = 87, CD = 17, CN = DK = 14.
1) Найдем AK. Очевидно, что AK = NB, и поэтому
AK = (AB - KN): 2,
но KN = CD как противоположные стороны прямоугольника, поэтому
AK = (AB - CD): 2 = (87 - 17): 2 = 35
2) Из треугольника ADK: тангенс угла A - это отношение противолежащего катета DK к прилежащему AK:
tg A = DK: AK = 14: 35 = 0,4
Ответ: 0,4
13)В треугольнике ABC угол C равен  ,
,  . Найдите синус внешнего угла при вершине B.
. Найдите синус внешнего угла при вершине B.

1) Некоторые формулы приведения:
sin (180o - x) = sin x cos (180o - x) = - cos x tg (180o - x) = -tg x ctg (180o - x) = - ctg x
2) Углы, сумма которых 90о, называются дополнительными. В нашей задаче это углы А и В. Дополнительные углы обладают таким свойством: sin B = cos A.
РЕШЕНИЕ
Рисунок к задаче см. на карточке-подсказке выше.
Поскольку углы А и В треугольника АВС являются дополнительными, то sin B =  .
.
Внешний угол при вершине B - это угол ABM. Поскольку углы ABM и ABC (угол ABC - это и есть угол B) смежные, то ABM = 180o - ABC, и
sin ABM = sin (180o - ABC) = sin ABC (т.е. -sin B) = 0,1
Ответ: 0,1
14) Найдите косинус угла AOB. В ответе укажите значение косинуса, умноженное на  .
.

РЕШЕНИЕ

1) Проведем АВ. Очевидно, что ОВ = АВ, потому треугольник АОВ равнобедренный. Проведем медиану ВМ. Она же по свойству медианы равнобедренного греугольника будет являться биссектрисой и высотой. Следовательно, треугольник ОВМ прямоугольный.
2) ОВ - гипотенуза красного треугольника на рисунке (с катетами 3 и 1), ОМ - гипотенуза зеленого треугольника (с катетами 2 и 1). Найдем по теореме Пифагора ОМ, ОВ и ВМ:

3) Из треугольника ОВМ: косинус угла АОВ - это отношение прилежащего катета ОМ к гипотенузе ОВ:

В ответ просят записать  .
.
Ответ: 2
P.S. Для доказательства того, что угол ВМО прямой, мы воспользовались свойством медианы равнобедренного треугольника. Но это можно доказать и по-другому. Достаточно заметить, что угол АМВ получается поворотом из прямого угла (относительно точки М), а значит, АМВ - тоже прямой угол, как и смежный с ним ВМО:

15) В треугольнике ABC угол A равен 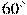 , угол B равен
, угол B равен  , CH — высота. Найдите разность углов ACH и BCH. Ответ дайте в градусах.
, CH — высота. Найдите разность углов ACH и BCH. Ответ дайте в градусах.

Сумма острых углов прямоугольного треугольника равна 90o.
РЕШЕНИЕ
Из треугольника АСН: сумма острых углов А и АСН равна 90o, откуда АСН = 90o - А = 90o - 60o = 30o.
Из треугольника ВСН: сумма острых углов В и ВСН равна 90o, откуда ВСН = 90o - В = 90o - 70o = 20o
Итак, АСН - ВСН = 30o - 20o = 10o
Ответ: 10
В7 1) Найдите значение выражения  .
.
Решение.
 .
.
Ответ: 5.
2) Найдите значение выражения  .
.
Решение.
По свойствам степеней имеем:
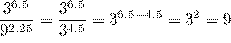 .
.
Ответ: 9.
3) Найдите значение выражения 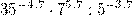 .
.
Решение.
 .
.
Ответ: 1,4.
4) Найдите значение выражения 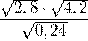 .
.
Решение.
 .
.
Ответ: 7.
5) Найдите значение выражения  .
.
Решение.
 .
.
Ответ: 2.
6) Найдите значение выражения  .
.
Решение.
 .
.
Ответ: -24.
7) Найдите значение выражения  .
.
Решение.
 .
.
Ответ: 2.
8) Найдите  , если
, если  и
и  .
.
Решение.
Поскольку угол альфа лежит в третьей четверти, его тангенс отрицателен. Поэтому
 .
.
Ответ: -3.
9) Найдите значение выражения  , если
, если 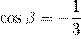 .
.
Решение.
 =
= 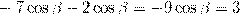 .
.
Ответ: 3.
10) Найдите значение выражения 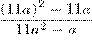 .
.
Решение.
 =
=  . Ответ: 11.
. Ответ: 11.
11) Найдите  , если
, если  .
.
Решение.
 .
.
Ответ: 1.
12) Найдите значение выражения  при
при  .
.
Решение.
 =
=  .
.
Ответ: 4.
13) Найдите значение выражения  .
.
Решение.
 =
=  .
.
Ответ: 8.
14) Найдите значение выражения  .
.
Решение.
 =
=  .
.
Ответ: 28.
15) Найдите значение выражения  .
.
Решение.
 =
= 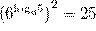 .
.
Ответ: 25.
16) Найдите значение выражения  .
.
Решение.
 =
=  .
.
Ответ: -0,5.
17) Найдите значение выражения  .
.
Решение.
 =
=  .
.
Ответ: -3.
18) Найдите значение выражения  .
.
Решение.
 =
=  .
.
Ответ: -1.
19) Найдите значение выражения  .
.
Решение.
 =
=






