Вращающий момент при s = l называется начальным пусковым моментом. Его значение найдем, подставив в (3-129) s = l:
. (3-134)
Уравнением (3-134) устанавливается зависимость М нач = f (
), которую мы будем рассматривать при изучении вопросов пуска в ход двигателей. Та же зависимость может быть получена из кривых рис. 3-44.
В предыдущем рассматривался электромагнитный момент, развиваемый ротором. При определении момента на валу нужно учесть механические (на трение) и добавочные потери, а также потери, вызванные пульсациями поля в зубцах статора и ротора. Практически электромагнитный момент мало отличается от полезного момента на валу, так как указанные потери незначительны.
3-14. Устойчивость работы машины
А) Двигатель.
Рассмотрим вначале вопрос об устойчивости работы трехфазного асинхронного двигателя. Напишем уравнение вращающих моментов, действующих на ротор двигателя при изменении его скорости вращения:
, (3-135)
где М — момент, развиваемый двигателем;
М ст — статический момент или момент сопротивления рабочего механизма, приводимого двигателем во вращение (с учетом потерь в самом двигателе);
— избыточный момент (положительный или отрицательный), обусловленный изменением кинетической энергии всех вращающихся частей двигателя и приводимого им во вращение механизма, имеющий общий приведенный к валу двигателя момент инерции J.
Момент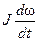 
называется также динамическим или моментом сил инерции. Выражение для него может быть получено следующим образом: кинетическая энергия вращающихся частей равна 
первая производная энергии по времени 
— мощность; мощность, деленная на угловую частоту, 
— динамический момент.
При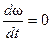 
и М изб = 0, следовательно, М - М ст = 0. В этом случае двигатель работает с постоянной частотой вращения, момент двигателя М уравновешивается статическим моментом М ст, т. е М = М ст. Однако практически указанное равенство не может сохраняться длительно. Всегда возможны возмущения режима, которые вызовут изменения М или М ст и, следовательно, изменение частоты вращения. Если по прекращении возмущения система (состоящая в данном случае из двигателя и механизма) стремится вернуться в исходное состояние и к нему возвращается, то она представляет собой устойчивую систему.
Обратимся к рис. 3-45, где представлена кривая момента двигателя M = f (n 2). Она легко может быть получена из ранее приведенной кривой M = f (s), так как n 2 = (1— s) n 1. На том же рисунке приведена пунктирная кривая M ст = f (п 2), соответствующая, например, изменению момента подъемного крана при изменении частоты вращения. Точки пересечения этой кривой с кривой момента двигателя получаются при равенстве М = М ст.
Рис. 3-45. К рассмотрению устойчивости работы асинхронного двигателя.
Правая точка соответствует устойчивой работе; здесь при возмущении, вызвавшем положительное приращение частоты вращения, возникает отрицательный избыточный момент 
, стремящийся замедлить вращение; при возмущении, вызвавшем отрицательное приращение частоты вращения, избыточный момент будет положительным, ускоряющим вращение. В левой точке устойчивая работа невозможна, так как здесь при отклонении частоты вращения в любую сторону возникает избыточный момент, действующий в ту же сторону.
Следовательно, неравенство
> 
или 
< 
(3-136)
может служить критерием устойчивости работы. При соблюдении этого неравенства работа будет устойчивой, при несоблюдении его — неустойчивой.
Б) Тормоз.
Обратимся к рассмотрению работы машины тормозом. Этот режим работы (при s > l) иногда применяется при необходимости быстро затормозить механизм, приводимый во вращение асинхронным двигателем. В этом случае применяется та же схема, что и при реверсировании двигателя (рис. 3-46).
Рис. 3-46. Схема для реверсирования двигателя (изменения направления вращения) и для перевода его в режим работы тормозом (для сокращения времени выбега).
Для перевода машины в тормозной режим нужно изменить в ней направление вращения поля, что делается при помощи показанного на рис. 3-46 переключателя.
Если тормозной режим используется только для быстрой остановки машины, то устойчивость этого режима не имеет значения; но иногда требуется длительная работа машины в режиме тормоза, например в случае, когда рабочим механизмом является подъемный кран. Такая работа также должна быть устойчивой. На рис. 3-47 приведены кривые M = f (s): 1 — при обычном сопротивлении , обмотки ротора, 2 — при увеличенном сопротивлении цепи ротора 
, где 
— добавочное сопротивление (приведенное к обмотке статора), вводимое в цепь ротора; здесь же приведена кривая M ст = f (s) подъемного крана.
Рис. 3-47. Устойчивость работы машины в тормозном режиме.
Очевидно, только при второй кривой M = f (s) работа в тормозном режиме будет устойчивой, так как здесь < . Следовательно, для устойчивой работы тормозом нужно в цепь ротора включить относительно большое сопротивление , что приводит также к уменьшению тока в обмотке ротора, а следовательно, и в обмотке статора.
3-15. Схемы замещения
Теория асинхронной машины основана на ее аналогии с трансформатором (§ 3-7 — 3-12). Необходимые величины и зависимости, характеризующие работу вращающейся машины, можно получить, заменив ее неподвижной машиной, работающей как трансформатор. При этом активное сопротивление роторной цепи, как указывалось, должно быть взято равным 
.
На основе полученных ранее уравнений мы можем получить, так же как для трансформатора, схему замещения асинхронной машины, позволяющую легко найти соотношения между величинами, характеризующими ее работу.
Обратимся к уравнению (3-123) и перепишем его в следующем виде:
. (3-137)
Выражению в скобках соответствует сопротивление схемы, приведенной на рис. 3-48.
Рис. 3-48. Схема замещения синхронной машины (Т-образная).
Уравнения напряжений и токов для этой схемы, составленные согласно законам Кирхгофа, будут такие же, как для машины [уравнения (3-115)— (3-117)]. Поэтому она называется схемой замещения асинхронной машины. Можем написать:
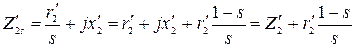, (3-138)
где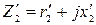 
— сопротивление роторной обмотки при s = l.
Активное сопротивление 
можно рассматривать как внешнее сопротивление, включенное в обмотку неподвижного ротора. Машина в этом случае работает как трансформатор, имеющий чисто активную нагрузку. Электрическая мощность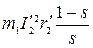 
, отдаваемая таким трансформатором, равна механической мощности 
, развиваемой ротором при работе машины, например двигателем со скольжением s, что следует из полученного ранее равенства (3-70 а) или (3-100).
Можно вместо схемы рис. 3-48 получить схему, более удобную для исследования асинхронной машины, позволяющую составить простые расчетные формулы для токов, мощностей, cos 
и построить круговую диаграмму.
Из схемы рис. 3-48 следует:
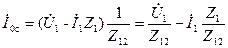. (3-139)
Подставив это значение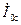 
в уравнение токов 
, получим:
;
отсюда имеем:
и
, (3-140)
где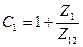 
[см. также (3-126)];
. (3-141)
— ток синхронизма, т. е. ток, потребляемый машиной при синхронной скорости вращения, при s = 0 (рис. 3-48).
Учитывая (3-141) и (3-127), перепишем уравнение (3-140) в следующем виде:
. (3-142)
Уравнениям (3-140) и (3-142) соответствует схема замещения, представленная на рис. 3-49.
Рис. 3-49. Г-образная схема замещения асинхронной машины.
Ее можно назвать Г-образной схемой замещения асинхронной машины. Она позволяет значительно проще, чем схема рис. 3-48, рассчитать токи 
и 
при любом значении s, так как здесь легко определяется ток 
, который не зависит от s. Исследование асинхронной машины при помощи приведенной на рис. 3-49 схемы замещения облегчается еще тем, что комплекс C 1 в обычных условиях можно заменить его модулем с,. Только при точных исследованиях малых машин (при Р н < 1 кВт) и в специальных случаях, когда аргумент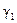 
в выражении С 1 = 
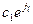больше 2—3°, следует его учитывать.
3-16. Параметры асинхронной машины
Параметры рассмотренных схем замещения являются в то же время параметрами асинхронной машины. Они могут быть определены расчетным или опытным путем.
При определении их расчетным путем нужно иметь геометрические размеры машины (наружный и внутренний диаметры статора, то же для ротора, длину воздушного зазора 
между статором и ротором, их длины по оси, а также размеры пазов и зубцов статора и ротора) и ее обмоточные данные (числа витков, их средние длины, сечения проводников и шаги обмоток, числа пазов). Мы будем здесь рассматривать только основные методы расчета параметров, имея в виду установить их связь с геометрическими размерами машины и ее электромагнитными нагрузками.
Под последними понимаются индукции в отдельных участках магнитной цепи машины, линейная нагрузка (условная величина), А/см,
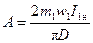, (3-143)
плотности тока для статорной и роторной обмоток: 
и 
, А/мм2.
