При разработке сложных изделий возникает необходимость в системном подходе к организации и проведению процесса проектирования изделий и разработки конструкторской документации.
В процессе автоматизированного решения той или иной задачи всегда участвуют 3 составляющие:
- комплекс технических средств;
- организационная система (коллектив организации);
- информационная среда.
В информационную среду входят организационное обеспечение (положения, приказы, требования); методическое обеспечение (документы, регламентирующие порядок эксплуатации САПР); математическое обеспечение (методы решения задач).
Разработка математического обеспечения является самым сложным этапом создания САПР, от которого в наибольшей степени зависит производительность и эффективность функционирования САПР в целом.
Программное обеспечение (совокупность всех программ и эксплуатационной документации к ним).
Решая ту или иную задачу, проектировщик использует все три компонента САПР. Отсутствие одного из этих компонентов не гарантирует успешного функционирования САПР.
Процесс проектирования состоит из нескольких последовательных этапов: разработка замысла изделия, определение его структуры, разбиение или декомпозиция изделия на элементы, каждому из которых ставится в соответствие своя задача.
Процесс решения задач можно вести несколькими способами: путем типового проектирования, модификационного проектирования, проектирования по заготовкам и путем оригинального проектирования.
При типовом проектировании функционирование САПР представляется как многотактная процедура формирования для каждой задачи своего проектного модуля и выполнение проектных операций на его базе.
В основе процедур формирования проектных моделей лежит использование информации о математических моделях элементов проектируемых изделий, представленных в предлагаемой базовой форме.
Для сложных изделий построить математические модели их элементов и разработать программы бывает трудно. В этих случаях можно прибегнуть к модификационному проектированию, которое основывается на использовании ранее получаемых технических решений, расположенных в архивах данных. В процессе проектирования просматривается архив, выбирается ближайший к задуманному варианту аналог и производится его редактирование, то есть модификация.
Существует способ проектирования по заготовкам. В этом случае из локальной базы данных задачи выбирается та или иная заготовка или основа – скелет будущего чертежа элемента изделия. Заготовка чертежа дополняется необходимыми элементами или корректируется до получения рабочего варианта. При проектировании данным способом требуется определенная квалификация и опыт разработчика.
В любом случае для более успешного решения задачи проектировщику необходимо знать методы и алгоритмы, реализованные в моделях и программах САПР.
САПР, как система используется проектировщиками не только на этапе разработки КД, но и на этапах изготовления и эксплуатации изделия, как средство хранения, оперативного поиска и корректировки КД.
Практическая реализация разработки и производства изделия как единого процесса, требует согласования всех его составляющих, в связи с чем создание САПР становится обязательной задачей.
9. Геометрические объекты. Аналитически не описываемые объекты
В приборостроении для отображения геометрических свойств деталей со сложными поверхностями применяют математические модели каркасные и кинематические.
Каркасные математические модели представляют собой каркасы – конечные множества элементов, например, точек или кривых, принадлежащих моделируемой поверхности. В частности, выбор каркаса в виде линий, образующих сетку на описываемой поверхности, приводит к разбиению поверхности на отдельные участки.
В кинематических математических моделях поверхность представляется в параметрическом виде R(U,V), где R = (α, y, z), а U и V – параметры. Такую поверхность можно получить как результат перемещения в трехмерном пространстве кривой R(U), называемой образующей, по некоторой направляющей линии. Коэффициенты уравнений, как правило, не имеют простого геометрического смысла, что затрудняет работу с ними в интерактивном режиме. Этот недостаток устраняется в канонических и геометрических макромоделях.
Канонические модели используют в тех случаях, когда удается выделить параметры, однозначно определяющие геометрический объект и в то же время имеющие простую связь с его формой. Например, для плоского многоугольника такими параметрами являются координаты времени, для цилиндра – направляющие косинусы и координаты некоторой точки оси, а также радиус цилиндра.
Геометрические макромодели являются описаниями предварительно отобранных типовых геометрических фрагментов. Такими фрагментами могут быть типовые сборочные единицы, а им макромоделями – условные номера, габаритные и стыковочные размеры. При оформлении конструкторской документации макромодели используют для описания типовых графических изображений, например, зубчатых колес, винтовых соединений, подшипников и т.д.
10. Конструирование с использованием ЭВМ.
Производительность ЭВМ, ее структура, связь с другими ЭВМ, количество и номенклатура внешних устройств определяют техническую производительность САПР. системное программное обеспечение управляет организацией вычислительного процесса на ЭВМ и обменом данными между различными устройствами и должно прежде всего удовлетворять требованиям и организации режима диалоговой обработки информации.
Ориентированные на решение конкретных задач САПР, например только на изготовление конструкторской документации, называют островными, или локальными системами. Они часто используются на начальной стадии внедрения САПР и могут быть реализованы в виде систем автоматизации разработки и выполнения конструкторской документации (АКД) со структурой и принципами построения. Аналогичными САПР. В интегрированной системе «проектирование – изготовление» объединяются подсистемы конструирования, геометрического регулирования, разработки технологии изготовления проектируемых изделий.
Под конструированием понимают разработку конструкции по предварительно выполненным проектным расчетам, осуществляемую в конструкторской документации. Цель конструирования – разработка и формирование изделий путем переработки геометрической, технологической и организационной информации.
Под геометрическим моделированием понимают создание моделей геометрических объектов (ГО), содержащих информацию о геометрии изделия – функциональную и вспомогательную. Информация о геометрических характеристиках геометрических объектов используется не только для получения графического изображения – двухмерной геометрической модели, но и для расчета различных характеристик. Объекта и технологических параметров его изготовления. Геометрическое моделирование является ядром автоматизированного конструирования и технологической подготовки производства. Разработка технологии изготовления проектируемых изделий обеспечивает реализацию превращения этой информации в изделие. Основой объединения подсистем является использование общей базы данных. Кроме того, каждая из подсистем должна иметь собственную базу данных, ориентированную на решение своих задач. Так, в системе конструирования должна быть ориентированная на конструирование система управления данными и база данных непосредственно по конструированию конкретного изделия.
Если раньше автоматизированные процессы проектирования создавались для решения проблем, ориентированных на изделие или учитывающих специфику производства, то последние разработки свидетельствуют о все увеличивающейся переориентации на создание универсальных методик и решение задач, входящих за пределы отдельных отраслей производства. Цель такой переориентации – пригодность отдельных систем для различных отраслей.
Различают два подхода к конструированию на основе компьютерных технологий.
Первый – основывается на двухмерной геометрической модели – графического изображения и использовании компьютера как электронного устройства, позволяющего значительно ускорить процесс конструирования и улучшить качество оформления конструкторской документации. Центральное место в этом подходе к конструированию занимает чертеж, который служит средством графического представления изделия, содержащего информацию для решения графических задач, а также для изготовления изделия.
Использование ЭВМ при решении графических задач должно быть рациональным и достаточно эффективным. Созданное на ЭВМ графическое изображение должно использоваться многократно или в различных вариациях, а формирование текстовых документов происходить автоматически в результате созданных чертежей и схем. С помощью ВТ обеспечиваются: оформление конструкторских документов, насыщенных изображениями стандартных, типовых, унифицированных составных частей (элементы принципиальных схем, печатных плат и т.д.); модернизация существующих конструкций (частичное изменение); разработка текстовых документов (спецификация, перечень элементов).
Второй – основан на компьютерной пространственной геометрической модели изделия, которая является более наглядным способом представления оригинала и более мощным и удобным инструментом для решения геометрических задач. Чертеж в этих условиях начинает играть вспомогательную роль, а методы его создания основаны на методах компьютерной графики, методах отображения пространственной модели.
11. Математическое обеспечение САПР. Метод половинного деления. Метод хорд
Метод половинного деления
Дано нелинейное уравнение:
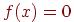
Найти корень уравнения, принадлежащий интервалу [a,b], с заданной точностью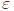 
.
Для уточнения корня методом половинного деления последовательно осуществляем следующие операции:
1. Делим интервал пополам:
2. В качестве нового интервала изоляции принимаем ту половину интервала, на концах которого функция имеет разные знаки.
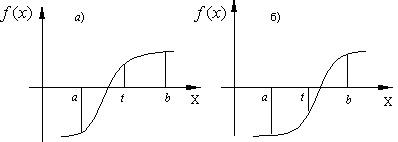
Для этого:
a) Вычисляем значение функции f(x) в точках a и t.
b) Проверяем: если f(a)f(t) < 0, то корень находится в левой половине интервала [a,b]. Тогда отбрасываем правую половину интервала и делаем переприсвоение b=t.
c) Если f(a)f(t) < 0 не выполняется, то корень находится в правой половине интервала [a,b]. Тогда отбрасываем левую половину и делаем переприсвоение a=t. В обоих случаях мы получим новый интервал [a,b] в 2 раза меньший предыдущего.
3.Процесс, начиная с пункта 1, циклически повторяем до тех пор, пока длина интервала [a,b] не станет равной либо меньшей заданной точности, т.е.
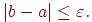
Метод хорд
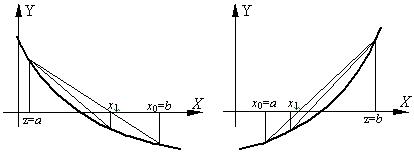
Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение корня.
При этом в процессе поиска семейство хорд может строиться:
а) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х0=b;
б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х0=a;
В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:
для случая а)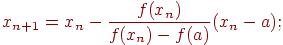 
(4.11)
для случая б)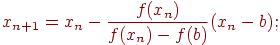 
(4.12)
Процесс поиска продолжается до тех пор, пока не выполнится условие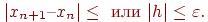 
(4.13)
Метод обеспечивает быструю сходимость, если f(z)f"(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и ее кривизны f"(z) совпадают.
