Приложение 2
Вычисление производной
Определение: Действие нахождения производной функции называется ее дифференцированием, а функцию, имеющую производную в точке х, называют дифференцируемой в этой точке.
Так как дифференцировать приходится функции с различным способом задания (в явном, неявном, параметрическом виде) и всякой степени сложности (основные элементарные, сложные, элементарные), то и подходы к решению подбираются в зависимости от ситуации.
В простейших случаях продифференцировать функцию можно с использованием определение производной, вычислив соответствующий предел. Этот метод можно назвать непосредственным дифференцированием.
Пример: Найти производную 
, используя определение.
Решение: Запишем предел отношения приращения функции к приращению аргумента и воспользуемся формулами тригонометрии:
Осталось применить первый замечательный предел для получения конечного результата:
Если Вам потребовалось найти производную одной из основных элементарных функций, то все они собраны в таблице основных производных и доказаны на основании определения.
Пример: Найти производные следующих постоянных функций
, 
, 
, 
, 
.
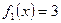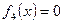Решение: Производные всех этих функций равны нулю для любого действительного x (на всей области определения)
, 
, 
, 
, 
.
При нахождении производных суммы, разности функций, их произведения или отношения к Вашим услугам правила дифференцирования. Их приходится использовать почти в каждой задаче.
Основные правила дифференцирования
Пусть с — константа, а u(х) и v(x) имеют производные в некоторой точке х. Тогда функции u(x)±v(x), c·u(x), u(x)·v(x) и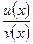 
(где v(x)≠ 0) также имеют производные в этой точке, причем:
1. (u±v)'=u'±v';
2. (и·v)'=u'v+uv', в частности, (с·и)'=с·и';
3. 
в частности 
.
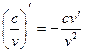Пример: Найти производную функции 
.
Решение: Из таблицы производных для тригонометрических функций видим 
. Воспользуемся правилом вынесения множителя за знак производной: 
.
Пример: Найти производную функции 
.
Решение: Упростим вид исходной функции 
.
Используем правило производной суммы (разности):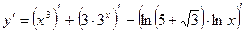 
Постоянный множитель можно выносить за знак производной, 
поэтому
Осталось воспользоваться таблицей производных:
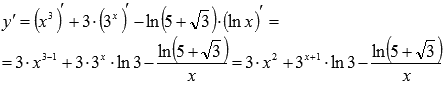Пример: Продифференцировать функцию 
.
Решение: В данном примере 
, 
. Применяем правило производной произведения:
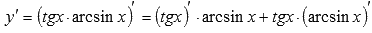
Обращаемся к таблице производных основных элементарных функций и получаем ответ:
Пример: Найти производную функции 
.
Решение: Исходная функция представляет собой отношение двух выражений sinx и 2x+1. Применим правило дифференцирования дроби:
.
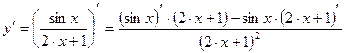Не обойтись без правил дифференцирования суммы и вынесения произвольной постоянной за знак производной:
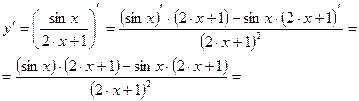
Если к таблице производных и правилам дифференцирования добавить формулу нахождения производной сложной функции, то вмести они позволят дифференцировать любую элементарную функцию, заданную в явном виде 
.
Производная сложной функции: у=f (u), u=g (x), тогда у =f (g (х)) – сложная функция. Найдем производную для этой функции 
Пример: Найти производную сложной функции 
.
Решение: В данном примере f – функция возведения в квадрат, а g(x) = 2x+1 – линейная функция.
Вот подробное решение с использованием формулы производной сложной функции:
;
Для дифференцирования показательно степенной функции 
очень удобно использовать логарифмическую производную. С ее помощью достаточно просто находятся и производные громоздких дробей.
Сначала производим логарифмирование по основанию e, упрощаем вид функции, используя свойства логарифма, и далее находим производную неявно заданной функции:
.
Пример: Найдите производную функции 
.
Решение: Воспользуемся формулой логарифмической производной:
Если функция представлена параметрическим способом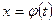 
, 
, 
, то ее дифференцирование производят по формуле: 
.
Пример: Найти производную параметрически заданной функции 
.
Решение: В данном примере 
, 
поэтому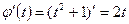 
, 
. Используем выведенную формулу и сразу записываем ответ: 
.
Ответ: 
.
Существует несколько способов дифференцирования неявно заданной функции вида 
.
Чтобы найти производную неявно заданной функции, необходимо продифференцировать обе части равенства по аргументу x, считая y – функцией от x, и после этого выразить 
.
Пример: Найти производную неявной функции 
.
Решение:
Производная неявно заданной функции всегда представляется в виде выражения, содержащего x и y: 
. Чтобы прийти к такому результату, продифференцируем обе части равенства:
Разрешим полученное уравнение относительно производной:
.
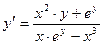