Позичкові проценти
Розрахунки за правилом складних процентів називають нарахуванням процентів на проценти, а процедуру приєднання нарахованих процентів – їх реінвестуванням або капіталізацією.
При рекурсивних процентах i нарощена сума через n періодів обчислюється за формулою:
 |
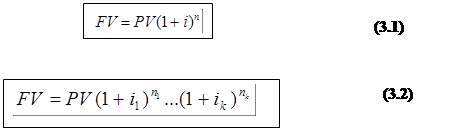а у випадку ставки процентів, що міняється від періоду до періоду,де i, i,…, і – процентні ставки за періоди n1, n2…, nn відповідно.
Приклад 1. Фірма одержала кредит на суму 100 млн. грн. терміном на 5 років на наступних умовах за схемою складних процентів:
- у перший рік процентна ставка складає 10.5%;
- для другого року передбачена надбавка до ставки в розмірі 1.5%;
- для третього року і наступних років – у розмірі 0.75%.
Визначте суму боргу наприкінці терміну позики.
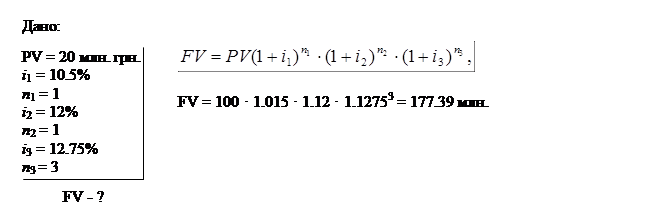
Вираз f n; i =(1+ i)n називається мультиплікуючим множником. Його також називають коефіцієнтом або множником нарощення. Зазначення його для різних значень ставки i і числа періодів n табульовані. Мультиплікуючий множник при будь – якій схемі нарахування процентів показує, у скільки разів збільшується початкова сума грошей при заданих процентній ставці і і кількості періодів нарощення процентів n.
Звичайно за процентний період береться один рік. Якщо проценти нараховуються кілька разів у році, а саме m разів, то говорять, що має місце m-кратне нарахування процентів.
У такій ситуації обговорюють не ставку за період, а річну ставку j, на основі якої обчислюють процентну ставку за період: j/m. Ставка j фактично потрібна тільки для того, щоб знати, яке число потрібно розділити на кількість періодів у році, щоб одержати ставку за період.
Базову ставку j називають при цьому номінальною. Подібна схема роботи характерна для банків.
Номінальна ставка не дозволяє зрозуміти, яка ж реальна прибутковість фінансової операції у виді повних річних процентів. У цьому випадку вводиться поняття ефективної ставки і.
Ефективна ставка дорівнює такій одноразовій річній процентній ставці, яка дозволяє одержати той самий результат фінансової операції, що і при нарахуванні процентів кілька разів у році. Інакше кажучи, ефективна ставка показує, скільки процентів за рік нараховано дійсно, якщо вони неодноразово приєднувалися, виходячи з номінальної ставки j.
 |
Виведемо співвідношення між номінальною й ефективною ставками позичкових процентів, виходячи з умови рівності нарощення:
Звідси, здійснюючи найпростіші обчислення, одержуємо формули (3.3) і (3.4), які дозволяють обчислювати ефективну ставку по заданій номінальній і навпаки.
Приклад 2. Є два внески: А і Б. По внеску А проценти нараховуються один раз на рік, виходячи з 120 % річних. По внеску Б проценти нараховуються по півріччях, виходячи з 100% річних. Порівняти прибутковості розміщення коштів.
Нарощена сума при внутрішній капіталізації m разів обчислюється за формулою:
| |||
| |||
Якщо термін фінансової операції визначений не в роках, а в днях або місяцях, а період нарахування процентів – один рік, то
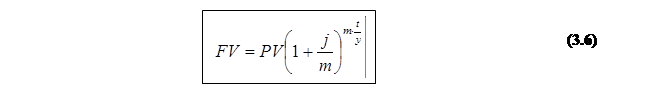
Якщо період не є рівним року, то, як і раніше, у формулі (3.6) t/y треба замінити на частину періоду l.
 |
Приклад 3. Яка ефективна ставка, якщо номінальна ставка дорівнює 25% при щомісячному нарахуванні процентів?
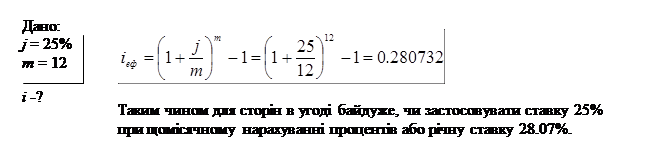Якщо загальне число інтервалів нарахування не є цілим числом, то для цілого числа періодів використовується формула складних процентів, а для залишку – або формула складних, або формула простих процентів, однак останнє застосовується частіше. Таким чином, якщо m·n – ціле, а l – частина інтервалу нарахування, то формула (3.5) приймає вид:
при нарахуванні простих процентів на частину періоду і вид:
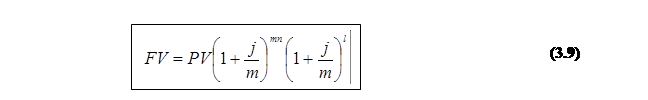при нарахуванні складних процентів на частину періоду.
Приклад 4. Інвестор одержав кредит у банку в розмірі 250 млн. грн. з терміном погашення через 2 роки 9 міс. (2 роки і 270 днів) під 9.5% річних. Визначити суму погашення при використанні банком складних процентів і змішаного методу нарахування процентів на неповний рік.
Авансові проценти.
Розглянемо тепер антисипативний спосіб нарахування складних процентів. Як і для звичайних процентів, тут уводиться поняття річної дисконтної ставки f.
У випадку банківського обліку дисконтних цінних паперів
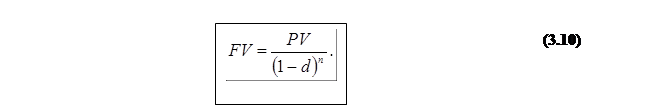
При нарахуванні процентів m разів на рік формула (3.11) приймає вид:
Якщо кількість періодів не ціле число, то
У формулі (3.12) m, n - ціла кількість інтервалів нарахування процентів, l – частина інтервалу нарахування, причому на неповний період тут нараховані прості проценти.
Які для позичкових процентів, потрібно обговорювати, які проценти нараховуються на неповний період, тому що можливо варіант нарахування складних процентів за формулою:
Як для позичкових, так і для авансових процентів, при стягуванні процентів кілька разів на рік може бути введене поняття ефективної авансової ставки. Виведемо співвідношення між номінальною й ефективною ставками авансових процентів, виходячи з умови рівності множників нарощення:
|
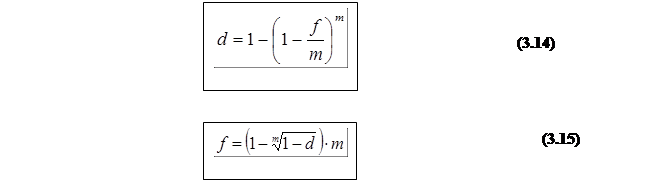
При безперервному нарахуванні процентів:
Приклад 5. Фінансовий інструмент на суму 5 мнл. грн., термін платежу по якому настає через 5 років, проданий з дисконтом по складній дисконтній ставці 15% річних. Яка сума дисконту? Визначити суму, отриману при поквартальному дисконтуванні по номінальній дисконтній ставці 15% і ефективну дисконтну ставку.
Рішення
У цьому прикладі – дві задачі. Перша може бути записана в такий спосіб:
Друга задача:
 |
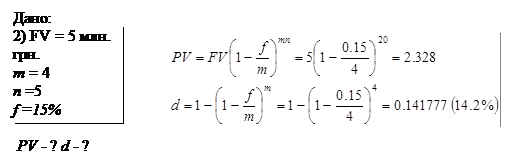