1) Если одна точка прямой лежит в плоскости, то все точки прямой лежат в этой плоскости;
2) через прямую и не лежащую на ней точку проходит плоскость, и притом только одна;
3) через две пересекающиеся прямые плоскость провести нельзя;
4) любые две плоскости не имеют общих точек;
5) если четыре точки не лежат в одной плоскости, то какие-нибудь три из них лежат на одной прямой.
56. Назовите общую прямую плоскостей AFD и DEF.
1) AD;
2) DE;
3) DF;
4) AF.
57. Через точку М, не лежащую на прямой а, провели прямые, пересекающие прямую а. Тогда:
1) эти прямые не лежат в одной плоскости;
2) эти прямые лежат в одной плоскости;
3) никакого вывода сделать нельзя;
4) часть прямых лежит в плоскости, а часть - нет;
5) все прямые совпадают с прямой а.
58.Прямая а лежит в плоскости α и пересекает плоскость β. Каково взаимное расположение плоскостей α и β?
1) они совпадают;
2) имеют только одну общую точку;
3) не пересекаются;
4) пересекаются по некоторой прямой.
59. Каким может быть взаимное расположение прямых а и b, если через прямую а можно провести плоскость, параллельную прямой b?
1) Скрещиваются или пересекаются;
2) пересекаются или параллельны;
3) скрещиваются или параллельны;
4) только скрещиваются;
5) только параллельны.
60. Прямые а и b пересекаются в точке М. Прямая с, не проходящая через точку М, пересекает прямые а и b. Что можно сказать о взаимном положении прямых а, b и c?
1) Все прямые лежат в разных плоскостях;
2) прямые а и b лежат в одной плоскости;
3) все прямые лежат в одной плоскости;
4) ничего сказать нельзя;
5) прямая с совпадает с одной из прямых: или с а, или с b.
61. Через концы отрезка АВ проведена плоскость. Через конец В и и точку С этого отрезка проведены параллельные прямые, пересекающие плоскость в точках В1 и С1. Найти длину отрезка ВВ1, если СС1=24 см, АС:ВС=3:6.
1)12
2)48
3)24
4)72
62. Через концы отрезка АВ и его середину М проведены параллельные прямые, пересекающие некоторую плоскость в точках А1, В1, М1. Найдите длину отрезка ММ1, если отрезок АВ не пересекает плоскость и если АА1=3,6 см, ВВ1=2,8 см.
1)3,2 см
2)2,7 см
3) 6,4 см
63. Дано: - плоскость; АВ – отрезок;
СÎАВ; АВÏa; АÎa; аÇa=С1
вÇa=В1; АС=ВС
ВВ1= 12,2см
Найти: СС1
1) 24, 4 см
2) 6,1 см
3) 12,2 см
64. Дано: a-плоскость; АВ – отрезок;
СÎАВ; АВÏa; АÎa; аÇa= С1
ВÇa= В1; АС:ВС=5:3
ВВ1= 24см
Найти: СС1
1) 15 см
2) 38,4 см
3) 40 см
- Найдите длину вектора
66. Найдите расстояние между точками E (-1,0,4) и F (2,-5,1).
1) 5 
.
2) 
.
3) 
.
4) 
.
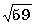67. Найдите координаты середины отрезка GH, если G (3,-2,0), H (0,-12,5).
1) ( 
,-5,5).
2) (3,-7,- 
).
3) ( ,-7, ).
4) (-3,7,- ).
- Найдите координаты вектора
, если I (5,-1,2), J ((3,-2,0).
1) (2,-1,2).
2) (-2,-1,2).
3) (2,-3,2).
4)(-2,-1,-2).
- Найдите длину вектора
, если K (0,-1,2), L (-3,5,0).
1) 
.
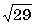2) 7.
3) 5.
4) 2 
.
- Найдите скалярное произведение векторов
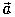(-5,6,1) и 
(0,-9,7).
1) –52.
2) 47.
3) –47.
4) –56.
- Найдите скалярное произведение векторов
- Найдите скалярное произведение векторов
- Скалярное произведение двух векторов равно нулю, если векторы:
1) параллельны
2) совпадают
3) перпендикулярны
- Выберите верное утверждение:
1) при сложении двух и большего числа векторов их одноименные координаты складываются;
2) если два вектора равны третьему вектору, то они совпадают;
3) любой вектор равен самому себе;
4) два вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых;
5) углом между двумя векторами называется угол между их направлениями
