Определение мощностей в ветвях

ПРОВЕРИЛ

 

Руководитель проекта ст.преп. ______________________ / Нефедова Н.В. /

^{(должность) (подпись) (Ф.И.О.)}

 

Санкт-Петербург

Расчет простой цепи переменного тока

 

Рис.1 Расчетная схема простой цепи переменного тока

Параметры схемы:

Частота вращения w = 2p f = 314 рад/c при f = 50 Гц.

Сопротивления R ₁ = 0 Ом, R ₂ = 10 Ом, R ₃ = 10 Ом.

Индуктивности L ₁ = 82,80 мГн, L ₂ = 114,65 мГн,

L ₃ = 82,80 мГн.

Емкости С ₁ = 199,1 мкФ, С ₂ = 122,5 мкФ, С ₃ = 88,5 мкФ.

В данном варианте задан закон изменения тока в 3-ей ветви:

,А

Требуется определить:

- комплексные сопротивления элементов сх- комплексные сопротивления ветвей схемы,

- токи во всех ветвях,

- напряжения между всеми указанными точками схемы,

-мощности всех ветвей схемы,

-суммарную мощность на входных зажимах,

- построить векторную диаграмму токов и напряжений.

 

1.Определение комплексных сопротивлений элементов схемы .

Индуктивные сопротивления:

Z_{L 1} = j w L ₁= j 314××10^-3 = j 2 5 Ом,

Z_{L 2} = j w L ₂= j 314×144,65×10^-3 = j 36 Ом,

Z_{L 3} = j w L ₃= j 314×82,8×10^-3 = j 2 6 Ом,

Емкостные сопротивления:

- j 15 Ом

- j 26 Ом

- j 36 Ом

Определение комплексных полных сопротивлений ветвей схемы.

Z ₁ = Z_{L 1} + Z_{C 1} = j 25 - j 15 = -j 10 Ом

Z ₂ = R ₂ + Z_{L 2} + Z_{C 2} = 10 + j 36 - j 26 = 10 + j 10 Ом

Z ₃ = R ₃ + Z_{L 3} + Z_{C 3} = 10 + j 26 - j 36 = 10 - j 10 Ом

В показательной форме записи комплексные сопротивления ветвей определяются с помощью следующих формул:

модуль А = , где a - действительная часть комплексного числа, b - мнимая часть комплексного числа; начальная фаза определяется с учетом знаков (т.е. квадранта).

Z ₁ = 10 e^{-j 90} Ом, Z ₂ = 14,41 e^{+j 45} Ом, Z ₃ = 14,41 e^-j45 ,Ом.

Определение комплексного действующего тока 1-ей ветви.

Действующее значение меньше амплитудного в раз. Мгновенное значение тока третьей ветви известно из исходных данных:

,А , А.

 

Тогда действующее значение тока 3-ей ветви

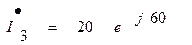, А.

Определение комплексного действующего напряжения 3-ей ветви.

, В.

Поскольку ветви 3 и 2 параллельны, то .

5.Определение комплексного д ействующего тока 2-ой ветви.

6. Определение комплексного действующего тока 1-ой ветви.

, .А

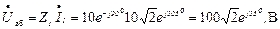7.Определение комплексного действующего напряжения 1-ой ветви.

 

8.Определение комплексного действующего напряжения на входе схемы U_аг.

, В.

Определение комплексного действующего напряжения между точками б, в и в, г

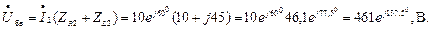
10. Определение комплексного действующего напряжения U_вг между точками в,г

, В.

Определение мгновенных значений токов и напряжений.

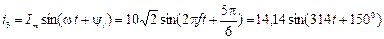- было задано

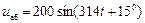
Определение мощностей в ветвях.

Общее выражение для определения полной мощности

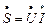, где ток берется комплекснымсопряженным.

Суммарная полная мощность схемы

13. Проверка баланса мощностей.

Активная мощность всей схемы (рис.1) должна быть равна сумме активных мощностей ветвей схемы, т.е. 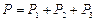, Вт.

Реактивная мощность всей схемы должна быть равна сумме реактивных мощностей ветвей схемы, т.е. , вар.

Согласно нашим расчетам получили:

P = 2000 Вт; P₁ + P₂ + P₃ = 0 + 1000 + 1000 = 2000, Вт.

Q = -2000 вар; Q₁ + Q₂ + Q₃ = -2000 + 1000 - 1000 = - 2000,вар

Баланс мощностей сошелся, следовательно, задача решена правильно.