Определение матрицы
-таблица чисел, записанная в виде
А11 А12 А13 А1n
А= А21 А22 А23 А2n
Аm1 Аm2 Аm3 Аnm m*n
Обозначается А=(а i J). Где а i J- элементы матрицы. I- указывает на номер строки, j- номер столбца.
Свойства матриц
1- сумма двух матриц
Суммой двух матриц А=(а i J) и В=(в i J) с одинаковым числом строк (m) и столбцов (n), называется новая матрица С=(с i J)., элементы которой определяются равенством
С (i J)=а i J+в i J причем С=(с i J) m*n, т.е. того же размера что и матрица А и В.Сумма двух матриц обозначается А+В=С
Аналогично определяется разность 2-х матриц
2- Умножение матрицы на число – чтобы умножить матрицу А=(а i J), на число λ, нужно умножить на это число все элементы матрицы
: λ А= λ (а i J)= (λ а i J)
3- Умножение 2-х матриц
Произведение матрицы А=(а i J) m*n и В=(в i J) k*n называется матрица С= (с i J)m*n у которой все элементы С i J = сумме произведений элементов i-той строки и матрицы А и j-ого столбца матрицы В
4- (А+В)*С= А*С +В*С
5- С(А+В) = С*А +С*В
6- А* (В*С)= (А*В)*С
7- (А+В) +С= А+ (В+С)
Определители матрицы и их вычисления
Обратная матрица
Понятие обратной матрицы вводится только для квадратных матриц
Если А квадратная матрица, то обратной для нее матрицей называется матрица обозначаемая А-1 удовлетворяющей условию А*А-1=А-1*А =Е
Системы m линейных уравнений с n переменн
(фигурная скобка)
а 11 * х1+ а 12* х2 +…..+ а 1n* хn= в 1
а21 *х1+а22* х2+….+а2n*xn=в2
…….
am1*x1 +am2*x2+….+amn*xn= вm
х1,х2, …, хn- неизвестные величины
аij- числа, называемые коэф. Системы
в1, в2,…, в n- числа называемые свободными членами.
№6 решение системы уравнений методом Крамера.
На практике используют формулы крамера,для решения систем уравнеий: Хi=Ai/|A| где (i= 1,2,…..n) эти формулы позволяют max неизвестные в виде дроби,знаменателем которых явл. Определитель матрицы системы,а числитель определитель матрицы ai, получили из А заменой столбца коэффициентов, при вычисляемом неизвестном,столбцов свободных членов.
№7 решение системы уравнений матричным методом.
Существует обратная матрица А-1. Умножив левую и правую части записи системы в матричной форме (А*Х=B) слева на А-1,,получен А-1(А*Х)=А-1B= (A-1*A)*X = A-1*B=E*X=A-1*B,а матрица умножается на единичную, получили X=A-1*B эта формула дает способ решения системы линейных уравнений,требующей отыскания, обратной матрицы и поэтому наз. Матричной.
№8 решение системы уравнений методом Гаусса.
Две системы содержащие одинаковое число неизвестных,наз. Равносильными,если они имеют равные множества решений. Алгоритм метода Гаусса!!!
1)среди коэф.системы выбирается любой отличный от 0 (обозн.его а pq)и назовем разрешающим элементом; p-тое уравнение наз. Разрешающим уравнением,q-тый столбец разрешающий столбец. Разрешающий элемент можно выбирать в тех уравнениях,кот.еще не были разрешающими.
2)разрешающее уравнение делится на разрешающий элемент в следствии чего разрешающий элемент =1.
3)путем послед. Умножения разрешающего уравнения на элементы разрешающего столбца, взятые с обратным знаком,и и последовательного почленного умножения p-ого уравнения со всеми(кроме самого p-ого)уравнениями системы, неизвестное Xq исключается из всех остальных уравнений системы в самом результате p –ом уравнении неизвестное Xq остается с коэф.= 1.
4)если в истеме есть ур-ие вида 0*х1+0*х2+…..0*хn=b. перейти к пункту 9.
5)если в системе есть ур-ие вида 0*х1+0*х2+…..0*хn=0,то оно исключается из системы.
6)если в системе есть уравнение кот.еще не были разрешающими,то перейти к пункту 1.
7)если число оставшихся в системе ур-ий (r)= числу неизвестных (n) Т.Е.r=n,то система после принимает вид ее ур-ие. Х1=В1
Х2=В2
………..
Хn=Вn система определена. Ее единств. Решением будет (В1,В2,В3,…..Вn) перейти к пункту 9.
8)если r<n,то система неопределенна и имеет бесконечное множество решений.перейти к пункту 9.
9) конец
векторы, координаты вектора, длина вектора.
А(x1,y1,z1); B(x2,y2,z2)
Координаты вектора АВ определяются: вектор АВ=(x2-x1,y2-y1,z2-z1)
Длина вектора -расстояние между началом и концом вектора. Обозначается вектор |AB| или |a|.
Если вектор а имеет координаты (x,y,z),то его длина определяется по формуле: вектор |a|= корень квадратный из x в квадрате, плюс y в квадрате, плюс z в квадрате.
длина нулевого вектора равна 0. Если длина вектора равна 1,то вектор называется единичный.
Действия над векторами.
Суммой вектора а и вектор в, называется вектор а+в, который идёт из начла вектора а в конец вектора в, при условии что вектор в приложен к концу вектора а.
Два вектора называются противоположными если их сумма равна нулевому вектору.
Разностью вектора а и вектора в называют вектор а-в, который представляет собой сумму вектора а и противоположный вектор (-в)
а-в=а+(-в) (сверху поставить чёрточку-вектор)
11 коллинеарность и перпендикулярность векторов, угол между ….
Два вектора называются коллинеарными если они лежат на одной прямой или на параллельных прямых.
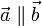Эти векторы могут быть направлены как одинаково так и противоположно.
Векторы являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю.
А(x1,y1,z1); B(x2,y2,z2)
x2*x1+y2*y1+z2*z1=0
Условия коллинеарности и перпендикулярности:
Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.
12.Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
Уравнение прямой L, проходящей через точку Мо (Хо; Уо) и перпендикулярной вектору n (А;В) имеет вид L А(Х-Хо) + В(У-Уо) = 0.
Замечание: Не нулевой вектор перпендикулярный данной прямой называется вектором нормали прямой.
13. Общее уравнение прямой.
Уравнение Ах + Ву + С = 0, при условии, что А2(в квадрате) + В2(в квадр.) не равно нулю (т. е. хотя бы одно из чисел А или В отлично от нуля) называется общим уравнением прямой. Таким образом каждой прямой соответствует уравнение первой степени с переменными Х и У:
1) Каждая прямая задается уравнением первой степени Ах+Ву+С=0, где хотя бы один их коэффициентов А или В отличен от нуля;
2) Каждое уравнение вида Ах+Ву+С=0, где хотя бы один коэф. А или В отличен от нуля, определяет прямую линию.
Замечание: Коэф. А и В в уравнении Ах+Ву+С=0 прямой явл. Координатами вектора нормали этой прямой.
14.Уравнение прямой, проходящей через данную точку пара….
Уравнение прямой L, проходящей через точку Мо (Хо; Уо) и \\ вектору а (р; q) имеет вид
L: Х-Хо = У-Уо;
р q
Замечание: Не нулевой вектор \\ данной прямой называется направляющим вектором прямой.
