А) Он минимизируется.
б) Он максимизируется.
в) Он не всегда дает однозначный ответ
95. Каких стратегий в матричной игре больше:
а) оптимальных.
б) чистых.
в) нет однозначного ответа.
96.В методе Брауна-Робинсон каждый игрок при выборе стратегии на следующем шаге руководствуется:
а) стратегиями противника на предыдущих шагах.
б) стратегиями противника в будущем.
в) своими стратегиями.
97. По критерию Вальда каждый игрок исходит из того, что:
а)случится наиболее плохая для него ситуация.
б) все ситуации равновозможны.
в) все ситуации возможны с некоторыми заданными вероятностями.
98. Антагонистическая игра может быть задана:
а) множеством стратегий игроков и ценой игры.
б) множеством стратегий первого игрока и функцией выигрыша второго игрока.
в) чем-то еще.
99. В графическом методе решения игр 3*3 для нахождения оптимальных стратегий игроков:
а) строится два треугольника.
б) строится один треугольник.
в) треугольники не строятся вовсе.
100 Если в антагонистической игре на отрезке [0;1] функция выигрыша 1-го игрока F(x,y) равна 2*x+C, то в зависимости от C:
а) седловых точек нет никогда.
б) седловые точки есть всегда.
в) иной вариант
101.Чем можно задать задачу принятия решения в условиях неопределенности на конечных множествах:
а) двумя матрицами.
б) выигрышами.
в) чем-то еще.
102. В антагонистической игре произвольной размерности выигрыш первого игрока – это:
а) число.
б) множество.
в) вектор, или упорядоченное множество.
г) функция.
103. В матричной игре 3*3 две компоненты смешанной стратегии игрока:
а) определяют третью.
б) не определяют.
104. Для какой размерности игровой матрицы критерий Вальда обращается в критерий Лапласа?
а)1*5
б)5*1
в)только в других случаях.
105. В чем отличие критерия Вальда от остальных изученных критериев принятия решения:
а) Он минимизируется
б) Он максимизируется
в) При расчете не используются арифметические операции сложения и вычитания.
106. Каких стратегий в матричной игре больше:
а) оптимальных.
б) не являющихся оптимальными.
в) нет однозначного ответа.
107. В методе Брауна-Робинсон каждый игрок при выборе стратегии на следующем шаге руководствуется:
а) стратегиями противника на предыдущих шагах.
б) своими стратегиями на предыдущих шагах.
в) чем-то еще.
108. По критерию математического ожидания каждый игрок исходит из того, что:
а) случится наихудшая для него ситуация.
б) все ситуации равновозможны.
в) все или некоторые ситуации возможны с некоторыми заданными вероятностями.
109. Антагонистическая игра может быть задана:
а) множеством стратегий игроков и ценой игры.
б) множеством стратегий обоих игроков и функцией выигрыша второго игрока.
в) чем-то еще.
110. Цена игры меньше верхней цены игры, если оба показателя существуют.
а) да.
б) не всегда.
в) никогда.
111. Если в антагонистической игре на отрезке [0;1]*[0;1] функция выигрыша 1-го игрока F(x,y) равна C (x-y)^2, то в зависимости от C:
а) седловых точек нет никогда.
б) седловые точки есть всегда.
в) третий вариант.
112. Могут ли в какой-то антагонистической игре значения функции выигрыша обоих игроков для некоторых значений переменных быть равны одному числу?
а)да, при нескольких значениях этого числа.
б) нет.
в) да, всего при одном значении этого числа.
113.Цена игры существует для матричных игр в смешанных стратегиях всегда.
а) да.
б) нет.
9.Каких стратегий в матричной игре размерности, отличной от 1*,
больше:
а) чистых.
б) смешанных.
114.Для матричной игры 
верно утверждение …
a. Стратегия В2 доминирует стратегию В3
b. Стратегия В3 доминирует стратегию В2
c. Стратегия В1 доминирует стратегию В4
d. Стратегия В4 доминирует стратегию В1
115.Для матричной игры 
верно утверждение …
a. Стратегия А2 доминирует стратегию А3
b. Стратегия А3 доминирует стратегию А2
c. Стратегия А1 доминирует стратегию А2
d. Стратегия А2 доминирует стратегию А1
116. Для матричной игры 
система уравнений для нахождения оптимальной стратегии 
игрока А и цены игры n имеет вид …
1) 
| 3) 
|
2) 
| 4) 
|
117.Для матричной игры 
система уравнений для нахождения оптимальной стратегии 
игрока В и цены игры n имеет вид …
1) 
| 3) 
|
2) 
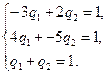
| 4) 
|
118.Графическое решение не допускается для матричной игры, платежная матрица которой имеет размерность …
e. 2х2
f. 2хn
G. mxn
h. mx2
119.Для решения матричной игры как задачи линейного программирования необходимо, чтобы …
i. Цена игры была положительной
j. Игра имела размерность 2х2
k. Сумма компонентов смешанных стратегий игроков равнялась 1
l. Игра не имела решения в чистых стратегиях
