Для этого выполните действия:
- начиная со строки 50, в ячейки столбцов А – Аргумент, В – Функция y=sin x, С– Функция y=cos x, D– Шаг введите исходные данные для аргумента и соответствующие формулы для вычисления значений функций;
- постройте сначала график функции y=sin x, затем добавьте на диаграмму методом перетаскивания график y=cos x;
Диаграмма должна иметь вид:
Как видно из диаграммы, система имеет на заданном отрезке единственное решение (одна точка пересечения).Для нахождение координат точки пересечения необходимо:
- навести указатель мыши на точку пересечения и щелкнуть левой кнопкой;
- появиться надпись с указанием искомых координат:
.
Таким образом, приближенное решение системы x=0.8; y= 0.697.
9. Самостоятельно решить задачу: Определить по какой цене необходимо продавать некоторый товар, чтобы спрос на него совпадал с его предложением, если известно, что зависимость спроса на товар y от его цены x выражается уравнением 
(кг.), а зависимость предложения товара z от его цены – уравнением 
(кг.). Цена товара может изменяться в диапазоне от 0,2 грн. до 3 грн. с шагом 0,2.
Т.е. решение задачи сводиться к нахождению координат точки пересечения графиков функций спроса и предложения. Начиная со строки 70, подготовьте исходные данные и решите систему уравнений.
Если Вы правильно решили эту задачу, то диаграмма должна иметь вид:
Координаты точка равновесия: x=1,6; y=3,56, т.е. при цене товара 1,6 грн. спрос и предложение товара равны друг другу и составляют 3,56 кг.
10. Вставьте новый лист Поверхность. На этом листе будут построены основные поверхности второго порядка: эллипсоид, г иперболоид и параболоид.
Канонические уравнения эллипсоида 
;
г иперболоида 
;
параболоида 
.
11. Постройте верхнюю часть эллипсоида 
, лежащую в диапазоне 
, 
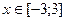с шагом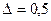 
для обеих переменных.
Для этого выполните действия:
- решить уравнение относительно z, т.е. найти 
;
- в ячейку А2 введите х, задайтевыравнивание по левому краю, в ячейку А1 – y, выровняйте по правому краю;
- нарисуйте диагональ в прямоугольнике А1: А2;
- в ячейки А3:А15 введитезначения х от -3 до 3 с шагом 0,5, используя автозаполнение;
- в ячейки В2:J2 аналогичновведитезначения y от -2 до 2 с шагом 0,5;
- в ячейку В3 введите формулу для вычисления значение переменной z, т.е. =КОРЕНЬ(1-$A3^2/9-B$2^2/4), ввод проводить в строке формул, обратите внимание, что имя столбца А и номер строки 2 фиксируются с помощью символов $;
- нажать кнопку ОК;
- ячейке В3 появиться #ЧИСЛО!, это означает что при х = -3 и y= -2 значение переменной z не определено (т.е. отрицательное значение под корнем);
- используя автозаполнение скопировать формулу из ячейке В3 в ячейки диапазона В3: J3, а затем в В3:J15;
Должна получить таблица:
- для диапазона ячеек В3:J15 построить диаграмму выбрав тип – Поверхность, вид – Проволочная (прозрачная) поверхность;
- на вкладке Ряд указать подписи по оси Х: диапазон А3:А15; в качестве имен Рядов указать значение переменной y, т.е. для Ряда 1 Имя: -2, для Ряда 2 Имя: -1,5 и т.д.;
- щелкните на кнопке Далее, введите Заголовкидиаграммы в соответствующих полях: Эллипсоид, Х, Y, Z;
- щелкните на кнопке Далее, Готово;
- уменьшите размер шрифта по осям; выполните форматирование.
Диаграмма должна иметь вид:
12. Самостоятельно ниже на этом же листепостройте верхнюю часть двухполостного гиперболоида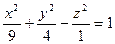 
, лежащую в диапазоне 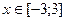, с шагом 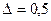для обеих переменных.
13. Самостоятельно нижепостройте часть гиперболического параболоида 
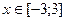, лежащую в диапазоне , с шагом 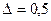для обеих переменных.
