Определение размера прибыли имеет в целом большое значение для предприятия, поскольку позволяет адекватно оценить финансовые ресурсы, объём платежей в бюджет, проанализировать возможности расширенного воспроизводства и материального стимулирования работников.
Наиболее гибким по отношению к динамике рынка является метод прогнозирования прибыли, основанный на анализе одиночных временных рядов, так как он позволяет учитывать изменение факторов, образующих прибыль.
Имеются данные о динамике рентабельности технологической продукции за последние пять лет.
| Год | |||||
| Рентабельность продукции, % | 19,7 | 20,1 | 19,4 | 20,3 | 21,0 |
Необходимо спрогнозировать уровень рентабельности продукции на 2004 г. [1].
Решение.
1. Будем производить отсчёт с 1999 года. Соответственно дополним данную таблицу строкой порядкового номера года (см. ниже).
| Порядковый номер года | |||||
| Год | |||||
| Рентабельность продукции, % | 19,7 | 20,1 | 19,4 | 20,3 | 21,0 |
Построим кривую по исходным точкам динамического ряда.
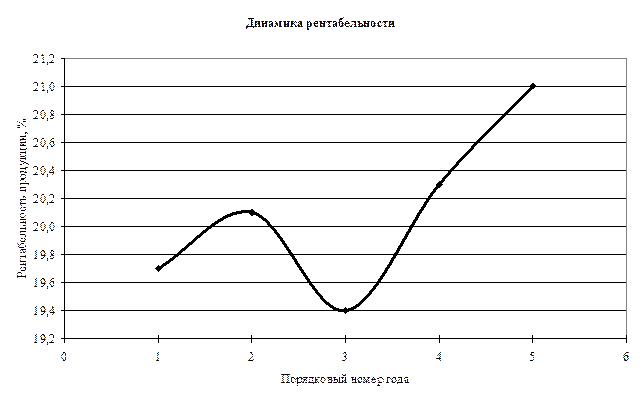
2. Осуществим выбор прогнозной модели, позволяющей указать наиболее вероятное значение уровня рентабельности технологической продукции на 2004 г. Для этого наложим на данный график линию тренда (линия тренда позволяет определить характер наблюдаемой динамики).
Стандартный пакет Microsoft Excel содержит 5 линий тренда (функциональных зависимостей):
1) линейную
y = a + bx;
2) логарифмическую
y = с ln x + b;
3) полиномиальную
y = b + c 1 x 1 + c 2 x 2 + … + cnxn;
4) степенную
y = c xb;
5) экспоненциальную
y = c e bx.
Здесь во всех функциональных зависимостях применительно к нашей задаче y – рентабельность продукции; x – год; a, b, c, ci (i = 1, 2, …, n) – константы.
Наряду с линией тренда, возможно отобразить и значение коэффициента детерминированности, или квадрата коэффициента корреляции R 2 (0 £ R 2 £ 1) (называемого также величиной достоверности аппроксимации), который показывает, насколько хорошо уравнение линии тренда описывает фактические данные. Полному совпадению прогнозируемых и фактических данных соответствует коэффициент детерминированности, равный 1.
Итак, наложим на кривую «Динамика рентабельности» линию тренда. Для этого правой кнопкой мыши активизируем экспериментальный график, и в появившемся меню выделим опцию Добавить линию тренда.

Наложим на экспериментальный график, например, линейную линию тренда. Тогда получим следующий рисунок.

Накладывая по очереди на экспериментальный график все вышеприведённые линии тренда, получим следующие их уравнения и коэффициенты аппроксимации.
| Линия тренда | Уравнение линии тренда | Коэффициент аппроксимации R 2 |
| Линейная | y = 0,28 x + 19,26 | 0,5227 |
| Логарифмическая | y = 0,5922 ln x + 19,5330 | 0,3777 |
| Полиномиальная (в данном случае квадратичная) | y = 0,1571 x 2 – 0,6629 x + 20,3600 | 0,7531 |
| Степенная | y = 19,54 x 0,0291 | 0,3727 |
| Экспоненциальная | y = 19,279 e 0,0138 x | 0,5158 |
Итак, по значению R 2 наиболее значимой оказывается полиномиальная линия тренда.
Однако, хотя из всех приведённых зависимостей коэффициент аппроксимации квадратичной зависимости и принимает наибольшее значение, но он меньше 0,9. А хорошим приближением считается такое, при котором значение коэффициента детерминированности больше 0,9 [2]. Поэтому наложим на экспериментальную кривую кубическую линию тренда.

Для данной задачи получим следующее уравнение линии тренда 3-го порядка:
y = 0,0750 x 3 – 0,5179 x 2 + 1,1071 x + 19,1000,
коэффициент аппроксимации которой
R 2 = 0,8071.
Как и для квадратичной зависимости, R 2 кубической линии тренда также не достигает значения 0,9. Однако рассмотрение полиномиальных зависимостей выше третьего порядка не имеет смысла, потому что экспериментальный график построен по пяти точкам, и любая линия тренда выше третьего порядка будет иметь (давать) коэффициент аппроксимации, равный 1.
Поэтому для решения данной задачи ограничимся кубической линией тренда, уравнение и коэффициент аппроксимации которой представлены выше.
3. Вычислим прогнозное значение рентабельности продукции на 2004 год: подставим в уравнение y = 0,0750 x 3 – 0,5179 x 2 + 1,1071 x + 19,1000 порядковый номер года, на который осуществляется прогноз, т.е. x = 6. В результате получим
y = 0,0750×63 – 0,5179×62 + 1,1071×6 + 19,1000 = 23,2982.
Прогноз рентабельности можно выполнить в Microsoft Excel следующим образом.
· Щелкнем правой кнопкой мыши по линии тренда и в появившемся меню выберем пункт Формат линии тренда.
· Выберем вкладкуПараметры и укажем Прогнозвперед на 1 единицу.
Результат действий представлен на нижерасположенном рисунке (линия тренда показана пунктиром).

Практически совпавшие линии свидетельствуют о правильности расчетов.
Таким образом, во-первых, найдена модель прогнозирования рентабельности продукции и степень её точности; во-вторых, определён уровень рентабельности продукции на 2004 г: его значение приблизительно равно 23,3.
Список литературы
1. Краснов А.Е., Красуля О.Н., Большаков О.В., Шлёнская Т.В. Информационные технологии пищевых производств в условиях неопределенности. – М.: ВНИИМП, 2001. – 496 с.
2. Орвис В. Excel для учёных, инженеров и студентов: Пер. с англ. – К.: Юниор, 1999. – 528 с.
1. Бражников А.М. Элементы научно-технического прогнозирования – М.: МТИММП, 1992.
2. Большаков О.В. и др. О введении операторных моделей в практику описания технологий в нормативно-технической документации // Мясная промышленность, 1994, № 5, с. 10 – 12.
3. Шаматов И.К. Формирование аналитических критериев для оценки инвестиционной привлекательности // Пищевая промышленность № 6, 2003. с. 41.






