по дисциплине «Моделирование»
Специальность 1-360901 «Машины и аппараты пищевых производств»
Проверил Выполнил
студент группы
Новик В. С.
«__»_________2012г. «__»_________2012г
Могилев 2012
Задание 1
1. Постановка задачи.
По заданным экспериментальным данным из m серий измерений по n измерений в каждой серии определить характеристики a и b математической модели объекта. Проверить адекватность полученного теоретического решения по критерию Фишера.
Схема взаимодействия объекта со средой:
x y=f(x) y
Экспериментальные данные:
| Параметр | X(i) | yji | ||||
| №(i) | y1i | y2i | y3i | y4i | y5i | |
| 0,157 | 0,197 | 0,167 | 0,177 | 0,147 | ||
| 0,09 | 0,13 | 0,1 | 0,11 | 0,08 | ||
| 0,061 | 0,101 | 0,071 | 0,081 | 0,051 | ||
| 0,046 | 0,086 | 0,056 | 0,066 | 0,036 | ||
| 0,035 | 0,075 | 0,045 | 0,055 | 0,025 | ||
| 0,028 | 0,068 | 0,038 | 0,048 | 0,018 | ||
| 0,023 | 0,063 | 0,033 | 0,043 | 0,013 | ||
| 0,019 | 0,059 | 0,029 | 0,039 | 0,009 | ||
| 0,016 | 0,056 | 0,026 | 0,036 | 0,006 | ||
| 0,014 | 0,054 | 0,024 | 0,034 | 0,004 |
2. Ход решения.
Исходное уравнение кривой имеет вид:
 (1)
(1)
Поделим уравнение (1) на 1 и получим:

Обозначим:




Вводя новые переменные получим уравнение
 ,(2)
,(2)
которое является уравнением прямой.
Расчет коэффициентов в уравнении (2) ведем по методу наименьших квадратов, т.к этот метод дает наименьшую ошибку аппроксимации опытных данных. Согласно этому методу коэффициенты 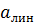 и
и  определяются:
определяются:
 (3)
(3)
 (4)
(4)
Расчёт сумм удобнее вести в табличной форме, предварительно определив средние значения функций  из m серий измерений:
из m серий измерений:
| Параметр | X | Yср | Xlin | Ylin | X² | X*Ylin |
| №(i) | ||||||
| 0,169 | - | 5,91716 | 5,91716 | |||
| 0,102 | - | 9,803922 | 19,60784 | |||
| 0,073 | - | 13,69863 | 41,09589 | |||
| 0,058 | - | 17,24138 | 68,96552 | |||
| 0,047 | - | 21,2766 | 106,383 | |||
| 0,04 | - | |||||
| 0,035 | - | 28,57143 | ||||
| 0,031 | - | 32,25806 | 258,0645 | |||
| 0,028 | - | 35,71429 | 321,4286 | |||
| 0,026 | - | 38,46154 | 384,6154 | |||
| Сумма | 0,609 | - | 227,943 | 1556,078 |
Подставив расчетные данные в формулы (3) и (4) получим:


Так как  , то a = 2,634
, то a = 2,634
Так как  то b = 3,665
то b = 3,665
Таким образом искомая эмпирическая зависимость будет иметь вид:
 (5)
(5)
Оценка адекватности состоит в сопоставлении полученной или предполагаемой теоретической функции  с результатами измерений.
с результатами измерений.
Для этого необходимо рассчитать экспериментальное (опытное) значение Критерия Фишера -  и сравнить его с теоретическим (табличным) -
и сравнить его с теоретическим (табличным) -  , принимаемым при требуемой доверительной вероятности
, принимаемым при требуемой доверительной вероятности  (обычно
(обычно  . Если
. Если  – модель адекватна, если
– модель адекватна, если  – модель неадекватна.
– модель неадекватна.
Экспериментальный критерий Фишера вычисляют по формуле
 (6)
(6)
где  дисперсия адекватности;
дисперсия адекватности;
 – средняя дисперсия всего эксперимента,
– средняя дисперсия всего эксперимента,


где  теоретическое значение функции для каждого измерения;
теоретическое значение функции для каждого измерения;
 – экспериментальное значение функции;
– экспериментальное значение функции;
 –среднее экспериментальное значение функции из m серий измерений;
–среднее экспериментальное значение функции из m серий измерений;
n – количество измерений в одном опыте (серии);
m – количество опытов (серий);
d – число коэффициентов уравнения теоретической регрессии.
Расчет сумм удобнее вести в табличной форме, предварительно определив по формуле (5) теоретические значения функции:
| Параметр | Yт | (Yт-Yэср)² | (Yт-Yэ1)² | (Yт-Yэ2)² | (Yт-Yэ3)² | (Yт-Yэ4)² | (Yт-Yэ5)² | Ʃ(Yт-Yэ5)² |
| №(i) | ||||||||
| 0,15872 | 0,000106 | 2,97E-06 | 0,00147 | 6,8E-05 | 0,0003 | 0,00014 | 0,002 | |
| 0,10035 | 2,74E-06 | 0,000107 | 0,00088 | 1,2E-07 | 9E-05 | 0,00041 | 0,0015 | |
| 0,07336 | 1,31E-07 | 0,000153 | 0,00076 | 5,6E-06 | 6E-05 | 0,0005 | 0,0015 | |
| 0,05782 | 3,39E-08 | 0,00014 | 0,00079 | 3,3E-06 | 7E-05 | 0,00048 | 0,0015 | |
| 0,04771 | 4,99E-07 | 0,000161 | 0,00074 | 7,3E-06 | 5E-05 | 0,00052 | 0,0015 | |
| 0,04061 | 3,67E-07 | 0,000159 | 0,00075 | 6,8E-06 | 5E-05 | 0,00051 | 0,0015 | |
| 0,03535 | 1,19E-07 | 0,000152 | 0,00076 | 5,5E-06 | 6E-05 | 0,0005 | 0,0015 | |
| 0,03129 | 8,49E-08 | 0,000151 | 0,00077 | 5,3E-06 | 6E-05 | 0,0005 | 0,0015 | |
| 0,02807 | 5,15E-09 | 0,000146 | 0,00078 | 4,3E-06 | 6E-05 | 0,00049 | 0,0015 | |
| 0,02545 | 2,99E-07 | 0,000131 | 0,00081 | 2,1E-06 | 7E-05 | 0,00046 | 0,0015 | |
| Сумма | - | 0,00011 | - | - | - | - | - | 0,0153 |
Подставив расчетные данные в формулу (6) получим:
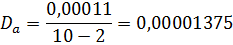


Значение  принимается по таблице 2 [8] для доверительной вероятности
принимается по таблице 2 [8] для доверительной вероятности  и числа степенной свободы
и числа степенной свободы  и
и  .
.
По условию задачи n = 10, d = 2 и m = 5
Тогда  и, соответственно,
и, соответственно, 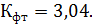
Так как  то модель адекватна экспериментальным данным (описываемому процессу).
то модель адекватна экспериментальным данным (описываемому процессу).






