Определение статических характеристик рассеяния измерений

Далее определяем выборочное среднее арифметическое (точнее оценка первого нейтрального выбора μ₁ или математического ожидания M(X))

≈ ≈

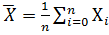В нашем случае после введения поправки выборочное среднее

арифметическое для исправленного ряда наблюдений должно быть равно Z

Мода M₀ в выборке – значение, которому соответствует максимум частоты. В нашем случае M₀= X_j=4=100,06 (см. табл. 8.3)

Медиана в выборке - результат наблюдения - среднее место в вариационном ряду. Обычно медиана определяется так

 

 

В нашем случае n/2=50; (n+2)/2=51; по вариационному ряду

100,06 +100,06)/2=100,06 В

Определяем точечную оценку дисперсии

S²= ≈ N_j.

Для нашего случая пользуясь таблице 8.3 имеем

Так как дисперсия имеет квадратичную размерность для большей наглядности пользуются средним квадратическим отклонением (СКО), точечная оценка которого определяется по формуле

S=

В нашем случае

=1,36 мА

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР. 52.12.38. 08

Точечная оценка СКО среднего арифметического значения определяется по выражению

=

Для нашего случая

= В

Определяем третий центральный момент выборки

μ₃= ≈ N_j

Для нашего случая имеем

Для относительной характеристики асимметрии используют безразмерный коэффициент асимметрии

γ₃= ≈

 

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР. 52.12.38. 08

Для нашего случая

γ₃= / = 0,048

Четвертый центральный момент выборки характеризует остро- или плосковершинность кривой распределения

μ₄= ≈ N_j

Для нашего случая пользуясь таблицей 8.3, находим

Относительное значение четвёртого нейтрального момента называется коэффициентом экцесса и находим его по формуле

γ₄= ≈

Эксцесс определяем по формуле

ξ= ≈

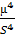
В нашем случае

γ₄= / 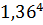-3= 0,26

ξ= / 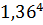= 3,26

Для классификации распределений по их форме удобней использовать другую функцию от эксцесса-контрэксцесс

K_э=1/

Для нашего случая

K_э=1/ =0,52

Таким образом получены все основные характеристики эпмирического распределения.

 

Проверка результатов измерений на наличие грубых погрешностей

Проверяем анормальность результатов наблюдений. Для этого берём крайние точки выборки и определяем зависимость.

 

Изм.

Лист

№ докум.

Подпись

Дата

Лист

КР. 52.12.38. 08

U₁= ; U_n=

Для нашего случая

U₁=(100-97,06)/ 1,36 =2,16<h=3,28

U₁₀₀=(100,06-100)/ 1,36 =0,044<h=3,28

 

Подбор теоретического распределения погрешности

Построение эмпирического распределение погрешности

Для нашего примера по таблице 8.3 построим гистограмму и для наглядного представления формы закона распределения погрешностей.

 

Рис.8.1. Распределение погрешностей