Призабойная область скважины (область вблизи ее стенок) подвержена воздействию многих факторов – глинистого раствора, воды, цемента, отложений парафина, солей и т.д., в результате чего уменьшается приток нефти и газа. Процесс бурения скважины ведет к перераспределению начального напряженного состояния горных пород, появляется аномальная зона вблизи скважины, что может привести к изменению фильтрационных свойств горных пород
В связи с этим необходимо рассчитать параметры этой аномальной зоны напряжения вблизи скважины.
Если горные породы считать однородным упругим телом, то задачу можно свести к решению задачи Ламе – расчету напряжений в однородном упругом толстостенном сосуде (см. рис.):
где rс – радиус скважины;
Pз – давление на забое (на стенки скважины).
Найдем решение задачи в перемещениях, приняв в качестве основной неизвестной функции радиальное перемещение U=U(r).
Тангенциальная компонента перемещений V в виду осевой симметрии отсутствует: V=0.
Обозначив 
из уравнения (24) получаем:
учитывая это, по закону Гука в полярных координатах (24), получаем:
(25)
Из уравнения равновесия (25) при R=T=0 (отсутствие внешних объемных нагрузок) остается только первое уравнение:
(26)
Подставив в уравнение (25) выражение (26), получим:
т.е. получим обыкновенное дифференциальное уравнение для перемещения U:
Его общим решением является функция:
где С1 и С2 – произвольные постоянные.
Отсюда по формулам (25) находим напряжения:
введем новые произвольные постоянные С и D соответственно:
Тогда:
Граничные условия задаем в следующем виде:
1. при r = rс (на стенке скважины): радиальное нормальное напрядение равно забойному давлению в скважине
(27)
2. при r =¥ (на бесконечности - радиальное нормальное напряжение равно горному давлению – это справедливо, если коэффициент бокового распора n = 1)
(28)
Из уравнений находим произвольные постоянные С и D:
Подставляя эти значения С и D в уравнение (28) найдем
Если коэффициент бокового распора n не равен 1, то учитывая, что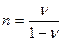 
, получим формулы:
(29)
(30)
Графики напряжений, построенные по формулам (29) и (30) имеют вид:
Из формул (29) и (30) видно, что на стенке скважины (r = rc)
(31)
(32)
т.е. на стенке скважины действуют касательные сжимающие напряжения, которые при РЗ=0 достигают двойного значения горного давления.
Следовательно, в призабойной зоне возможно разрушение непрочных горных пород под действием сжимающих тангенциальных напряжений и ухудшение фильтрационных свойств пород.
Из формулы (32) видно, что стенки ствола скважины или шахты будут устойчивы, если:
где sСЖ – предел прочности породы при двухосном сжатии.
Процессы усложняются при проявлении пластичных свойств горных пород.
Как видно из выше предложенного рисунка, область аномальных напряжений невелика – практически лишь в несколько раз превосходит размеры горной выработки.
