| Колебаниями называются: | ||
| процессы в той или иной мере повторяющиеся во времени; | 1 | |
| процесс изменения координаты по закону синуса или косинуса; | ||
| изменение заряда конденсатора по закону синуса или косинуса; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Механические колебания – это: | ||
| колебания маятников, струн, частей машин и т.д.; | 1 | |
| колебания переменного электрического тока в цепи, векторов напряженности и магнитной индукции и т.д.; | ||
| колебания мембраны телефона, диффузора электродинамического громкоговорителя и т.д.; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Электромагнитные колебания - это: | ||
| колебания маятников, струн, частей машин и т.д.; | ||
| колебания переменного электрического тока в цепи, векторов напряженности и магнитной индукции и т.д.; | 1 | |
| колебания мембраны телефона, диффузора электродинамического громкоговорителя и т.д.; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Электромеханические колебания – это: | ||
| колебания маятников, струн, частей машин и т.д.; | ||
| колебания переменного электрического тока в цепи, векторов напряженности и магнитной индукции и т.д.; | ||
| колебания мембраны телефона, диффузора электродинамического громкоговорителя и т.д.; | 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Свободными колебаниями называются колебания: | ||
| которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния её устойчивого равновесия; | 1 | |
| которые возникают в какой-либо системе под влиянием переменного внешнего воздействия; | ||
| при которых значение всех физических величин, характеризующих колебательную систему и изменяющихся при её колебаниях, повторяются через равные промежутки времени; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Вынужденными колебаниями называются колебания: | ||
| которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния её устойчивого равновесия; | ||
| которые возникают в какой-либо системе под влиянием переменного внешнего воздействия; | 1 | |
| при которых значение всех физических величин, характеризующих колебательную систему и изменяющихся при её колебаниях, повторяются через равные промежутки времени; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Периодическими называются колебания: | ||
| которые происходят в отсутствии переменных внешних воздействий на колебательную систему и возникают вследствие какого-либо начального отклонения этой системы от состояния её устойчивого равновесия; | ||
| которые возникают в какой-либо системе под влиянием переменного внешнего воздействия; | ||
| при которых значение всех физических величин, характеризующих колебательную систему и изменяющихся при её колебаниях, повторяются через равные промежутки времени; | 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Периодом колебания называется: | ||
| промежуток времени, за который фаза колебаний получает приращение 2·π; | 1 | |
| промежуток времени, за который фаза колебаний получает приращение π; | ||
| количество колебаний, совершаемых за время, равное 2·π; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную формулу для периода колебаний: | ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верные единицы измерения периода колебаний: | ||

| 1 | |

| ||

| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Частотой колебаний называется: | ||
| число полных колебаний, совершаемых в единицу времени; | 1 | |
| число полных колебаний, совершаемых за время 2·π; | ||
| число полных колебаний, совершаемых за время π; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную формулу: | ||

| 1 | |
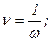
| ||

| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную формулу для частоты колебаний: | ||
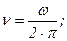
| 1 | |

| ||

| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать единицы измерения частоты: | ||

| ||

| ||

| 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Частота периодического процеcса 1 Гц – это частота: | ||
| при которой за 1 с совершается 1 цикл процесса; | 1 | |
| при которой за 1 с совершается π циклов процесса; | ||
| при которой за π с совершается 1 цикл процесса; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Циклической частотой называется: | ||
| число полных колебаний за 2·π с; | 1 | |
| число полных колебаний за 1 с; | ||
| число полных колебаний за π с; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Единицами измерения циклической частоты являются: | ||

| 1 | |
| Гц; | ||
| м/с; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Гармоническими называются колебания: | ||
| которые происходят по закону синуса или косинуса; | 1 | |
| при которых координата не изменяется с течением времени; | ||
| которые подчиняются законам Ньютона; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать уравнение гармонических колебаний: | ||
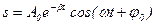 ; ;
| ||
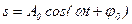 ; ;
| 1 | |
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний  см, амплитуда колебаний равна: см, амплитуда колебаний равна:
| ||
| 25 см; | 1 | |
| 28 см; | ||
| 28π см; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний 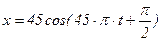 см, циклическая частота колебаний равна: см, циклическая частота колебаний равна:
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний  см, период колебаний равен: см, период колебаний равен:
| ||
 ; ;
| 1 | |
 ; ;
| ||
| 24 с; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний  см, частота колебаний равна: см, частота колебаний равна:
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний  см, фаза колебаний в момент времени t равна: см, фаза колебаний в момент времени t равна:
| ||
 ; ;
| 1 | |
 ; ;
| ||
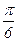 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний  см, начальная фаза колебаний равна: см, начальная фаза колебаний равна:
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний  см. Зависимость скорости от времени может быть дана в виде: см. Зависимость скорости от времени может быть дана в виде:
| ||
 см/с; см/с;
| 1 | |
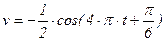 см/с; см/с;
| ||
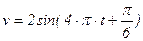 см/с; см/с;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний  см. Максимальная скорость при таких колебаниях равна см. Максимальная скорость при таких колебаниях равна
| ||
 ; ;
| 1 | |
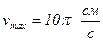 ; ;
| ||
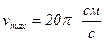 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Зависимость скорости от времени задана уравнением  см/с. Выбрать верную зависимость координаты от времени: см/с. Выбрать верную зависимость координаты от времени:
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Зависимость скорости от времени задана уравнением  см/с. Определить амплитудное значение смещения: см/с. Определить амплитудное значение смещения:
| ||
| 3 см; | 1 | |
| 36 см; | ||
| 18 см; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний  см. Определить зависимость ускорения от времени: см. Определить зависимость ускорения от времени:
| ||
 ; ;
| 1 | |
 ; ;
| ||
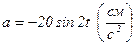 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Дано уравнение гармонических колебаний 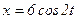 см. Определить амплитуду ускорения: см. Определить амплитуду ускорения:
| ||
 ; ;
| 1 | |
 ; ;
| ||
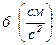 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть материальная точка массой m=10 г совершает гармонические колебания по закону  м. Определить зависимость возвращающей силы от времени: м. Определить зависимость возвращающей силы от времени:
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть материальная точка массой m=10 г совершает гармонические колебания по закону  м. Определить амплитудное значение возвращающей силы: м. Определить амплитудное значение возвращающей силы:
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Система, совершающая гармонические колебания, называется: | ||
| гармоническим осциллятором; | 1 | |
| физическим маятником; | ||
| гармоническим колебатором; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Амплитудой колебания называется: | ||
| максимальное значение колеблющейся величины; | 1 | |
| минимальное значение колеблющейся величины; | ||
| зависимость колеблющейся величины от времени; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выберите на графике изображение гармонического колебания: | ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выберите на графике изображение затухающего колебания: | ||
 ; ;
| ||
 ; ;
| 1 | |
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть материальная точка массой m совершает гармонические колебания по закону 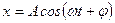 , тогда её кинетическая энергия , тогда её кинетическая энергия
| ||
изменяется по закону  ; ;
| 1 | |
изменяется по закону  ; ;
| ||
не изменяется с течением времени и равна  ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть материальная точка массой m совершает гармонические колебания по закону 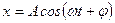 , тогда её потенциальная энергия , тогда её потенциальная энергия
| ||
изменяется по закону  ; ;
| ||
изменяется по закону  ; ;
| 1 | |
не изменяется с течением времени и равна  ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть материальная точка массой m совершает гармонические колебания по закону 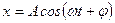 , тогда её полная энергия , тогда её полная энергия
| ||
изменяется по закону  ; ;
| ||
изменяется по закону  ; ;
| ||
не изменяется с течением времени и равна  ; ;
| 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Метод векторных диаграмм заключается в следующем: | ||
из некоторой точки О под углом φ откладывают вектор  длиной, равной амплитуде колебаний. Если вращать этот вектор с частотой ω, то его проекция изменяется по закону: длиной, равной амплитуде колебаний. Если вращать этот вектор с частотой ω, то его проекция изменяется по закону: 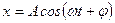 ; ;
| 1 | |
из некоторой точки О под углом ωt+φ откладывается вектор  , что позволяет изображать в каждый момент времени t смещение точки как совокупность векторов , что позволяет изображать в каждый момент времени t смещение точки как совокупность векторов 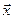 ; ;
| ||
из некоторой точки О под углом  , где А – амплитуда, откладыва6ется вектор , где А – амплитуда, откладыва6ется вектор  частоты. Таким образом, получается частотное изображение гармонических колебаний; частоты. Таким образом, получается частотное изображение гармонических колебаний;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Под сложением колебаний понимают: | ||
| нахождение закона результирующих колебаний системы в тех случаях, когда эта система одновременно участвует в нескольких колебательных процессах; | 1 | |
| нахождение закона результирующего колебания, когда на колебательную систему действует переменная вынуждающая сила; | ||
| нахождение законов колебаний материальных точек когда они являются составляющей одной системы; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать векторную диаграмму, изображающую сложение сонаправленных колебаний: | ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Пусть разность фаз складываемых сонаправленных колебаний равна 0. Амплитуда А1=7 см, а А2=2 см. Амплитуда результирующего колебания равна: | ||
| А=9 см; | 1 | |
| А=5 см; | ||
| А=14 см; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Пусть А1 и А2 амплитуды двух сонаправленных колебаний, Ф1(t) и Ф2(t) – соответственно фазы этих колебаний. Тогда амплитуда результирующего колебания при сложении этих колебаний равна: | ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Колебания, у которых разность фаз равна 0, называются: | ||
| синфазными; | 1 | |
| когерентными; | ||
| происходящими в противофазе; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Колебания, у которых разность фаз не изменяется с течением времени t, называются: | ||
| синфазными; | ||
| когерентными; | 1 | |
| происходящими в противофазе; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Если разность фаз колебаний равна π, то колебания называются: | ||
| синфазными; | ||
| когерентными; | ||
| происходящими в противофазе; | 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Биениями называются: | ||
| негармонические колебания, получающиеся в результате наложения двух одинаково направленных гармонических колебаний с близкими частотами; | 1 | |
| негармонические колебания, получающиеся в результате наложения двух одинаково направленных гармонических колебаний с одинаковыми частотами; | ||
| негармонические колебания, получающиеся в результате наложения двух одинаково направленных гармонических колебаний с частотами, отличающимися на 2π; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать функцию, описывающую биения: | ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Циклической частотой биения называется величина: | ||
 ; ;
| 1 | |
 ; ;
| ||
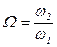 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Частота биения определяется по формуле: | ||
 ; ;
| 1 | |
 ; ;
| ||
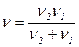 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Период биений определяется по формуле: | ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выберите графическое изображение биений: | ||
 ; ;
| ||
 ; ;
| ||
 ; ;
| 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть частица участвует в двух взаимно перпендикулярных колебаниях 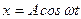 и и  , тогда уравнение результирующей траектории имеет вид: , тогда уравнение результирующей траектории имеет вид:
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть частица участвует в двух взаимно перпендикулярных колебаниях 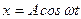 и и  , тогда результирующая траектория представляет собой: , тогда результирующая траектория представляет собой:
| ||
| эллипс; | 1 | |
| параболу; | ||
| гиперболу; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть частица участвует в двух взаимно перпендикулярных колебаниях 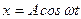 и и  , причём , причём  , тогда уравнение результирующей траектории имеет вид: , тогда уравнение результирующей траектории имеет вид:
| ||
 ; ;
| ||
 ; ;
| 1 | |
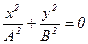 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть частица участвует в двух взаимно перпендикулярных колебаниях 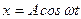 и и  , причём , причём  . Выбрать верное изображение траектории: . Выбрать верное изображение траектории:
| ||
 ; ;
| ||
 ; ;
| 1 | |
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть частица участвует в двух взаимно перпендикулярных колебаниях 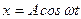 и и  , причём , причём 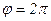 , тогда уравнение результирующей траектории имеет вид: , тогда уравнение результирующей траектории имеет вид:
| ||
 ; ;
| 1 | |
 ; ;
| ||
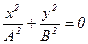 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть частица участвует в двух взаимно перпендикулярных колебаниях 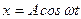 и и  , причём , причём 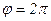 . Выбрать верное изображение траектории: . Выбрать верное изображение траектории:
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть частица участвует в двух взаимно перпендикулярных колебаниях 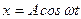 и и  , причём , причём  , тогда уравнение результирующей траектории имеет вид: , тогда уравнение результирующей траектории имеет вид:
| ||
 ; ;
| ||
 ; ;
| ||
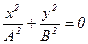 ; ;
| 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Пусть частица участвует в двух взаимно перпендикулярных колебаниях 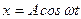 и и  , причём , причём  . Выбрать верное изображение траектории: . Выбрать верное изображение траектории:
| ||
 ; ;
| ||
 ; ;
| ||
 ; ;
| 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную запись дифференциального уравнения гармонических колебаний: | ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную запись дифференциального уравнения затухающих колебаний: | ||
 ; ;
| ||
 ; ;
| 1 | |
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную запись дифференциального уравнения вынужденных колебаний: | ||
 ; ;
| ||
 ; ;
| ||
 ; ;
| 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
В формуле  , ,  ‑ это: ‑ это:
| ||
| циклическая частота колебания; | 1 | |
| коэффициент затухания колебания; | ||
| коэффициент релаксации колебания; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Выбрать эквивалентную запись уравнения  : :
| ||
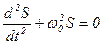 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
Выберите верное решение дифференциального уравнения  : :
| ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Физическим маятником называется: | ||
| твёрдые тала, колеблющиеся под действием силы тяжести вокруг горизонтальной оси, не проходящей через центр масс тела; | 1 | |
| материальная точка, подвешенная на длинной тонкой нерастяжимой нити и совершающая колебания под действием силы тяжести; | ||
| груз, закреплённый на пружине и совершающий гармонические колебания под действием силы упругости; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Математическим маятником называется: | ||
| твёрдые тала, колеблющиеся под действием силы тяжести вокруг горизонтальной оси, не проходящей через центр масс тела; | ||
| материальная точка, подвешенная на длинной тонкой нерастяжимой нити и совершающая колебания под действием силы тяжести; | 1 | |
| груз, закреплённый на пружине и совершающий гармонические колебания под действием силы упругости; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную формулу для определения периода физического маятника: | ||
 ; ;
| 1 | |
 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную формулу для определения периода математического маятника: | ||
 ; ;
| ||
 ; ;
| 1 | |
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верную формулу для определения периода пружинного маятника: | ||
 ; ;
| ||
 ; ;
| ||
 ; ;
| 1 | |
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
В формуле  , J –это: , J –это:
| ||
| момент инерции; | 1 | |
| момент силы тяжести; | ||
| ускорение свободного падения; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
В формуле  , l –это: , l –это:
| ||
| длина нити; | 1 | |
| расстояние от точки подвеса физического маятника до центра масс; | ||
| длина пружины; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Приведенная длина физического маятника – это физическая величина, равная: | ||
 ; ;
| 1 | |
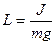 ; ;
| ||
 ; ;
| ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
В формуле  , l –это: , l –это:
| ||
| длина нити; | ||
| расстояние от точки подвеса физического маятника до центра масс; | 1 | |
| длина пружины; | ||
| ф.ф | Эту строку лучше оставить для удержания размеров и правильности оформления границ | |
| Выбрать верное утверждение: | ||
| приведенная длина физического маятника – это длина такого математического маятника, у которого период колебаний равен периоду физического маятника; | 1 | |
| приведенная длина физического маятника – это расстояние от точки подвеса маятника до его центра масс; | ||
| < |

Поиск:
Рекомендуем:
 Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ
Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки)
Нейроглия (или проще глия, глиальные клетки)
Категории:
текст может вставляться любой
|
|
|
|
|
|
|
|
|
Дата добавления: 2016-09-06; Мы поможем в написании ваших работ!; просмотров: 269 | Нарушение авторских прав
Поиск на сайте:
Лучшие изречения:

