Лекция 5. Физико-химические методы изучения макромолекул
Движению частиц (молекул) в жидкой фазе препятствует сила трения об молекулы растворителя и растворенных веществ. Это сила вызывает эффект, называемый вязкостью. Всем реальным жидкостям и газам присуща вязкость (внутренне трение). Растворы, содержащие макромолекулы, имеют большую вязкость, чем чистый растворитель. Возрастание вязкости является функцией ряда параметров макромолекулы, каждый из которых увеличивает инкремент вязкости. Такими параметрами являются объем молекулы (объем раствора, который вытесняет молекула), осевое соотношение (отношение длины молекулы к ширине), жесткость структуры макромолекулы. Поэтому определение показателей вязкости растворов макромолекул позволяет судить об этих параметрах. Удобными моделями для описания поведения макромолекул в жидкой среде являются модели правильной сферы, эллипсоида вращения, жесткого стержня (Рис.1). Так, для глобулярных белков объем макромолекулы можно связать с массой макромолекулы.
Рис.1. Физические модели макромолекул:
1- сфера радиусом r; 2 – вытянутый эллипсоид вращения, а > в; 3 - сплющенный эллипсоид, а < в; 4- вытянутый стержень, а< < в
В случае тонких длинных молекул (например, фибриллярные белки, ДНК), основной эффект на вязкость раствора оказывает осевое соотношение и оно является функцией молекулярной массы. Следовательно, измерение вязкости растворов макромолекул (вискозиметрия) может быть использована для определения молекулярной массы, или, если м.м. известна, то по вязкости раствора можно судить об общей длине молекулы.
Рассмотрим эффект вязкости на следующей модельной схеме. Жидкость помещена между двумя параллельными пластинами, одна из которых неподвижна, а другая движется со скоростью V по направлению Х (рис. 2). Слой жидкости, прилегающий к первой пластине, будет двигаться со скоростью примерно равной V, слой жидкости, прилегающий к нижней пластине будет двигаться со значительно меньшей скоростью. Представим, что жидкость между пластинами состоит из большого количества тонких (мономолекулярных) слоев, каждый из которых скользит вдоль соседнего.
Возникающее трение между слоями приводит к появлению градиента скорости. Вид деформации в движущихся жидкостях, вызванный градиентом скорости, называют сдвигом. И. Ньютон показал, что сила сопротивления f между соседними слоями пропорциональна градиенту скорости dV/dY, размеру площади соприкосновения слоев S, коэффициенту вязкости h:
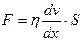[1]
где dv/dx - изменение скорости отнесенное к расстоянию между слоями в направлении, перпендикулярном скорости (градиенту модуля скорости), S - площадь соприкосновения слоев, h - динамическая вязкость жидкости (коэффициент вязкости - зависит от формы молекул, температуры среды).
 | ||||||||||||||
| ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 | ||||||||||||||
 |
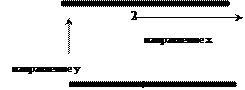Б
Рис. 2. Модель ламинарного течения жидкости между двумя пластинами (А) и в цилиндрической трубе (Б) (Фрайфельдер, 361 с)
1. –пластина, движущаяся со скоростью v; 2- неподвижная пластина; 3.- жидкость, состоящая из бесконечно тонких слоев (длина стрелки отражает скорость движения слоя);
Ньютоновой жидкостью является вода, гомогенные водные растворы неорганических и органических соединений.
К неньютоновским жидкостям относятся жидкости, состоящие из сложных и крупных молекул (полимеров). Например, кровь, представляющая собой раствор молекул неорганических веществ, белков, углеводов и специализированных клеток. В жидкостях внутреннее трение обусловлено действием межмолекулярных сил. Расстояния между молекулами жидкости сравнительно невелики, а силы взаимодействия значительны. Молекулы жидкости, подобно частицам твердого тела, колеблются около положения равновесия, но эти положения равновесия не являются постоянными. По истечении времени “оседлой жизни” молекула скачком переходит в новое положение. Среднее время “оседлой жизни” молекул называется временем релаксации t. С повышением температуры и понижением давления время релаксации уменьшается, что обуславливает подвижность жидкости и ее малую вязкость. Зависимость вязкости от температуры имеет сложный характер. Чем чаще молекулы меняют свои положения равновесия, тем более текуча и менее вязка жидкость, т.е. вязкость жидкости прямо пропорциональна времени релаксации h~t. Если жидкость течет по цилиндрической трубе, наибольшее трение испытывает слой у стенок трубки. В этом случае скорость течения максимальна вдоль центральной оси трубки и минимально вдоль стенок. Градиент скорости носит не линейный, параболический характер(Рис. 2, Б). Для протекании жидкости через трубку требуется некоторая разность давлений. Зависимость между объемом жидкости, протекающей за время t через трубку длиной l и разностью давлений Dp на концах трубки, выражается формулой Пуазейля:
V = pr4Dp t/ 8 hl [2]
где r - радиус трубки, l - длина трубки, h - динамическая вязкость жидкости. Для определения вязкости жидкости по этой формуле необходимо, чтобы течение было ламинарным, т.е. таким, при котором слои жидкости текут не перемешиваясь. Для вихревого (турбулентного) движения формула Пуазейля несправедлива. Чтобы при обычных скоростях вихри не появлялись, трубка должна быть достаточно тонкой. Приборы, с помощью которых определяют вязкость, называются вискозиметрами. Измерение входящих в формулу Пуазейля величин r, l, Dp провести трудно и поэтому прибегают к определению вязкости жидкости методом сравнения ее движения в данном вискозиметре с движением эталонной жидкости с известной вязкостью.
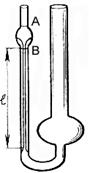
Одно колено капиллярного вискозиметра Оствальда представляет собой капиллярную трубку (рис. 3). В широкое колено вискозиметра вливают воду, а затем грушей всасывают воду в другое колено так, чтобы ее уровень был выше отметки А. Сняв грушу, наблюдают за понижением уровня воды. Когда мениск проходит через отметку А, включают секундомер, при прохождении метки В - выключают. Так находят время t0 прохождения воды между метками А и В. Оно будет равно времени прохождения этого объема через капилляр. Также определяют время t протекания исследуемой жидкости. Объем жидкости берут равным объему воды. Жидкости в капилляре движутся под действием гидростатического давления Dр = rgh, где r - плотность жидкости, h - разность уровней давления жидкости в двух коленах вискозиметра. Для равных объемов жидкости, протекающих через капилляр, можно записать V = pr4Dp0t0/(8n0l), откуда pr4Dp0t0/(8n0l) = pr4Dpt/(8nl), или
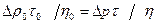[3]
Подставляя Dp0 = r0gh, Dp = rgh в формулу [3], получим:
r0ght0/h = rght/h или ght0/n0 = ght/n, откуда
n = n0t/t0 [4]
где n -кинематическая вязкость исследуемой жидкости (n = h/р), n0 - кинематическая вязкость воды (0,105 ×10-2 м2/с), t - время истечения исследуемой жидкости, t0 - время истечения воды.
Обозначим постоянную прибора А = n 0/t0 [5].
Тогда формула [4] примет вид n = At.
Вязкость раствора может значительно отличаться от вязкости растворителя. Добавление молекул к растворителю с вязкостью h0 приводит к повышению вязкости раствора до величины h. Изменение вязкости в этом случае выражают как отношение h/h0, называемое относительной вязкостью hотн.
|
|
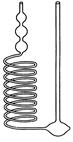
Рис. 3. Каппилярный визкозиметр Оствальда (1), многошариковый визкозиметр (2) (описание в тексте)
Вязкость раствора может значительно отличаться от вязкости растворителя. Добавление молекул к растворителю с вязкостью h0 приводит к повышению вязкости раствора до величины h. Изменение вязкости в этом случае выражают как отношение h/h0, называемое относительной вязкостью hотн.
Вязкость часто выражают как удельную вязкость hуд, которая является долей изменения вязкости, вызванная только добавлением растворенного вещества, тогда
hуд = h - h0 / h0 = hотн –1 [6]
По величине этого показателя можно судить о свойствах молекул растворенного вещества. Биологические молекулы представляют собой полимерные молекулы. В растворах этих молекул большую роль играют них межмолекулярные взаимодействия, которые увеличиваются с ростом концентрации. Относительная и удельная вязкости растворов непосредственно не связаны с параметрами макромолекул (формой, объемом). Для характеристики макромолекул используют еще один показатель вязкости, которую называют характеристической (внутренней) вязкостью [h]:
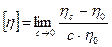= lim hуд/с @ аV [6]
где hс - вязкость раствора полимера, h0 - вязкость растворителя, а - константа, зависящая от формы молекулы, V - константа, характеризующая объем молекулы. Как видно, характеристическая вязкость зависит только от константы а, связанной с формой молекулы и от удельного объема V. Для разбавленных растворов характеристическая вязкость запишется так
[h] = νVN0/M [7]
где М – молекулярная масса макромолекулы, N0 = число Авагадро, V = объем макромолекулы, ν - фактор формы макромолекулы (коэффициент Симхи)
Экспериментальноопределяют удельную вязкость при нескольких концентрациях, строят график зависимости hуд /с от с и экстраполируют к с = 0.
Гибкие цепи макромолекул в растворе принимают форму асимметрического клубка, который можно представлять в виде эллипсоида вращения. Такая молекула вращается вместе с жидкостью, пронизывающий данный клубок. Характеристическая вязкость такой молекулы зависит от молекулярной массы. Для полимеров одного гомологичного ряда в определенном растворителе существует зависимость [h] = k0M, где k0 - постоянный коэффициент, М - молекулярная масса. Показатель степени ассимитричности зависит от формы молекул. Для шарообразных молекул а = 0. Чем сильнее асимметрия клубка, тем больше а. Уравнение [5] можно записать в виде ln[h] = ln k + a ln M. Оно представляет собой уравнение прямой [h] = f(M) в логарифмических координатах. Измерив характеристическую вязкость нескольких растворов полимеров одного гомологичного ряда с известными М и построив график зависимости [h] = f(M), можно определить неизвестную молекулярную массу вещества.
Для определения характеристической вязкости используется многошариковый вискозиметр (рис. 4). Он отличается от вискозиметра Оствальда тем, что имеет более длинный капилляр и позволяет более точно измерить время протекания жидкости. Наличие трех шариков позволяет создавать различные градиенты скорости.
В системе СИ значения вязкости h (динамической вязкости) выражают в Паּс (паскаль-секунд), внесистемная единица измерения h - П (пуаз): 1 Паּс = 10 П. Вязкость воды при 20º С составляет 1 мПаּс, большинства низкомолекулярных жидкостей доходит до 10 мПаּс. Вязкость крови человека в норме 4-5 мПаּс, при патологии колеблется в пределах 1,7 – 23 мПаּс. Отношение динамической вязкости к плотности жидкости называется кинематической вязкостью n. Единицей измерения n в системе СИ является м2/с (квадратный метр в секунду), внесистемной единицей – Ст (стокс): 1 м2/с =10000 Ст. Кинематическая вязкость полнее, чем динамическая, учитывает влияние внутреннего трения на характер течения жидкости или газа в трубах. Характер течения жидкости или газа существенно зависит от размеров трубы. В широких трубах даже при небольших скоростях течения может возникнуть турбулентное движение. Например, в трубке диаметром 2 см течение воды становится турбулентным при скорости 12 см/с, а в трубке с диаметром 2 мм – только при скорости 127 см/с. Течение крови в артериях человека является ламинарным, небольшая турбулентность возникает вблизи клапанов. При патологии, вследствие уменьшения вязкости крови, движение крови в сосудах может стать турбулентным. Для характеристики движения жидкости в трубах удобно использовать показатель - число Рейнольдса Re.
Re = ρvD/h = vD/n
