Момент импульса и закон его сохранения

При сравнении законов вращательного и поступательного движений просматрива­ется аналогия между ними, только во вра­щательном движении вместо силы «вы­ступает» ее момент, роль массы играет момент инерции. Какая же величина будет аналогом импульса тела? Ею является момент импульса тела относительно оси.

Моментом импульса (количества дви­жения) материальной точки А относитель­но неподвижной точки О называется физи­ческая величина, определяемая векторным произведением:

L = [ rp | = [ r m v ],

 

 

где r — радиус-вектор, проведенный из точки О в точку A; p = m v — импульс ма­териальной точки (рис.28); L —псевдо­вектор, его направление совпадает с на­правлением поступательного движения правого винта при его вращении от r к p. Модуль вектора момента импульса

L = rp sinalfa =mvr sinalfa= pl,

где a — угол между векторами r и p, l — плечо вектора р относительно точки О.

Моментом импульса относительно не­подвижной оси z называется скалярная величина L_z, равная проекции на эту ось вектора момента импульса, определенного относительно произвольной точки О дан­ной оси. Значение момента импульса L_z не зависит от положения точки О на оси z.

При вращении абсолютно твердого те­ла вокруг неподвижной оси z каждая от­дельная точка тела движется по окружно­сти постоянного радиуса r_i с некоторой

скоростью v_i. скорость v_i; и импульс m _iv_i

перпендикулярны этому радиусу, т. е. ра­диус является плечом вектора m_i v _i. Поэто­му можем записать, что момент импульса отдельной частицы

L_iz = т_iv_ir_i (19.1)

и направлен по оси в сторону, определяе­мую правилом правого винта.

Момент импульса твердого тела отно­сительно оси есть сумма моментов импуль­са отдельных частиц:

Используя формулу (17.1) v_i = wr_i, получим

т. е.

L_z = J_zw. (19.2)

Таким образом, момент импульса твердого тела относительно оси равен произведе­нию момента инерции тела относительно той же оси на угловую скорость.

Продифференцируем уравнение (19.2) по времени:

т. е.

dL_z/dt= M_z

Это выражение — еще одна форма урав­нения (закона) динамики вращательного движения твердого тела относительно неподвижной оси: производная момента импульса твердого тела относительно оси равна моменту сил относительно той же оси.

Можно показать, что имеет место век­торное равенство

d L /dt= М. (19.3)

В замкнутой системе момент внешних сил М =0 и d L /dt=0, откуда

L = const. (19.4)

Выражение (19.4) представляет собой закон сохранения момента импульса: мо­мент импульса замкнутой системы сохра­няется, т. е. не изменяется с течением времени.

Закон сохранения момента импуль­са — фундаментальный закон природы, Он связан со свойством симметрии про­странства — его изотропностью, т. е. с ин-

 

 

вариантностью физических законов отно­сительно выбора направления осей коор­динат системы отсчета (относительно поворота замкнутой системы в простран­стве на любой угол).

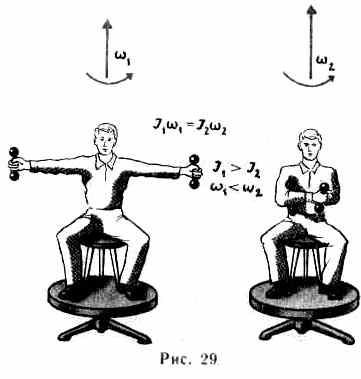
Продемонстрировать закон сохране­ния момента импульса можно с помощью скамьи Жуковского. Пусть человек, сидя­щий на скамье, которая без трения враща­ется вокруг вертикальной оси, и держа­щий в вытянутых руках гантели (рис. 29), приведен во вращение с угловой скоро­стью w₁. Если человек прижмет гантели к себе, то момент инерции системы умень­шится. Поскольку момент внешних сил равен нулю, момент импульса системы со­храняется и угловая скорость вращения w₂ возрастает. Аналогично, гимнаст во время прыжка через голову поджимает к тулови­щу руки и ноги, чтобы уменьшить свой момент инерции и увеличить тем самым угловую скорость вращения.

Сопоставим основные величины и уравнения, определяющие вращение те­ла вокруг неподвижной оси и его поступа­тельное движение (табл.2).

Свободные оси. Гироскоп

Для того чтобы сохранить положение оси вращения твердого тела с течением време­ни неизменным, используют подшипники, в которых она удерживается. Однако существуют такие оси вращения тел, кото­рые не изменяют своей ориентации в про­странстве без действия на нее внешних сил. Эти оси называются свободными ося­ми (или осями свободного вращения). Можно доказать, что в любом теле су­ществуют три взаимно перпендикулярные оси, проходящие через центр масс тела, которые могут служить свободными осями (они называются главными осями инерции тела). Например, главные оси инерции однородного прямоугольного параллеле­пипеда проходят через центры противопо­ложных граней (рис. 30). Для однородно­го цилиндра одной из главных осей инер­ции является его геометрическая ось, а в качестве остальных осей могут быть две любые взаимно перпендикулярные оси, проведенные через центр масс в плоско­сти, перпендикулярной геометрической оси цилиндра. Главными осями инерции шара

 

 

являются любые три взаимно перпендику­лярные оси, проходящие через центр масс.

Для устойчивости вращения большое значение имеет, какая именно из свобод­ных осей служит осью вращения.

Можно показать, что вращение во­круг главных осей с наибольшим и наи­меньшим моментами инерции оказывается устойчивым, а вращение около оси со средним моментом — неустойчивым. Так, если подбросить тело, имеющее форму параллелепипеда, приведя его одновре­менно во вращение, то оно, падая, будет устойчиво вращаться вокруг осей 1 и 2 (рис. 30).

Если, например, палочку подвесить за один конец нити, а другой конец, закреп­ленный к шпинделю центробежной маши­ны, привести в быстрое вращение, то па­лочка будет вращаться в горизонтальной плоскости около вертикальной оси, пер­пендикулярной оси палочки и проходящей через ее середину (рис.31). Это и есть свободная ось вращения (момент инерции при этом положении палочки максималь­ный). Если теперь палочку, вращающуюся вокруг свободной оси, освободить от внеш­них связей (аккуратно снять верхний ко­нец нити с крючка шпинделя), то положе­ние оси вращения в пространстве в тече­ние некоторого времени сохраняется. Свойство свободных осей сохранять свое положение в пространстве широко при­меняется в технике. Наиболее интересны в этом плане гироскопы — массивные од­нородные тела, вращающиеся с большой угловой скоростью около своей оси сим­метрии, являющейся свободной осью.

Рассмотрим одну из разновидностей гироскопов — гироскоп на кардановом подвесе (рис.32). Дискообразное тело — гироскоп — закреплено на оси АА, кото­рая может вращаться вокруг перпендику­лярной ей горизонтальной оси ВВ, кото­рая, в свою очередь, может поворачивать­ся вокруг вертикальной оси DD. Все три оси пересекаются в одной точке С, являю­щейся центром масс гироскопа и остаю­щейся неподвижной, а ось гироскопа мо­жет принять любое направление в про­странстве. Силами трения в подшипниках всех трех осей и моментом импульса колец пренебрегаем.

Так как трение в подшипниках мало, то, пока гироскоп неподвижен, его оси можно придать любое направление. Если начать гироскоп быстро вращать (напри­мер, с помощью намотанной на ось вере­вочки) и поворачивать его подставку, то ось гироскопа сохраняет свое положение в пространстве неизменной. Это можно объяснить с помощью основного закона динамики вращательного движения. Для свободного вращающегося гироскопа сила тяжести не может изменить ориентацию его оси вращения, так как эта сила при­ложена к центру масс (центр вращения С совпадает с центром масс), а момент силы тяжести относительно закрепленного центра масс равен нулю. Моментом сил трения мы также пренебрегаем. Поэтому если момент внешних сил относительно его закрепленного центра масс равен нулю, то, как следует из уравнения (19.3), L =

 

 

= const, т. е. момент импульса гироскопа сохраняет свою величину и направление в пространстве. Следовательно, вместе с ним сохраняет свое положение в про­странстве и ось гироскопа.

Чтобы ось гироскопа изменила свое направление в пространстве, необходимо, согласно (19.3), отличие от нуля момента внешних сил. Если момент внешних сил, приложенных к вращающемуся гироскопу относительно его центра масс, отличен от нуля, то наблюдается явле­ние, получившее название гироскопичес­кого эффекта. Оно состоит в том, что под действием пары сил F, приложенной к оси вращающегося гироскопа, ось ги­роскопа (рис. 33) поворачивается вокруг прямой О₃О₃, а не вокруг прямой О ₂ О ₂, как это казалось бы естественным на первый взгляд (O ₁ O ₁и О ₂ О ₂лежат в плоскости чертежа, а О₃О₃ и силы F перпендикуляр­ны ей).

Гироскопический эффект объясняется следующим образом. Момент М пары сил F направлен вдоль прямой О ₂ О ₂. За время dt момент импульса L гироскопа получит приращение d L = M dt (направление d L совпадает с направлением М) и станет рав­ным L' = L +d L. Направление вектора L ' совпадает с новым направлением оси вра­щения гироскопа. Таким образом, ось вра­щения гироскопа повернется вокруг пря­мой О₃О₃. Если время действия силы мало, то, хотя момент сил М и велик, изменение момента импульса d L гироскопа будет также весьма малым. Поэтому кратковременное действие сил практически не при­водит к изменению ориентации оси враще­ния гироскопа в пространстве. Для ее изменения следует прикладывать силы в течение длительного времени.

Если ось гироскопа закреплена под­шипниками, то вследствие гироскопиче­ского эффекта возникают так называемые гироскопические силы, действующие на опоры, в которых вращается ось гироско­па. Их действие необходимо учитывать при конструировании устройств, содержа­щих быстровращающиеся массивные со­ставные части. Гироскопические силы имеют смысл только во вращающейся си­стеме отсчета и являются частным случаем кориолисовой силы инерции (см. §27).

Гироскопы применяются в различных гироскопических навигационных приборах (гирокомпас, гирогоризонт и т. д.). Другое важное применение гироскопов — поддер­жание заданного направления движения транспортных средств, например судна (авторулевой) и самолета (автопилот) и т. д. При всяком отклонении от курса вследствие каких-то воздействий (волны, порыва ветра и т. д.) положение оси ги­роскопа в пространстве сохраняется. Сле­довательно, ось гироскопа вместе с рама­ми карданова подвеса поворачивается от­носительно движущегося устройства. По­ворот рам карданова подвеса с помощью определенных приспособлений включает рули управления, которые возвращают движение к заданному курсу.

Впервые гироскоп применен француз­ским физиком Ж. Фуко (1819—1868) для доказательства вращения Земли.

Деформации твердого тела

Рассматривая механику твердого тела, мы пользовались понятием абсолютно твердо­го тела. Однако в природе абсолютно твердых тел нет, так как все реальные тела под действием сил изменяют свою форму и размеры, т. е. деформируются.

Деформация называется упругой, если после прекращения действия внешних сил тело принимает первоначальные размеры и форму. Деформации, которые сохраня-

 

 

ются в теле после прекращения действия внешних сил, называются пластическими (или остаточными). Деформации реально­го тела всегда пластические, так как они после прекращения действия внешних сил никогда полностью не исчезают. Однако если остаточные деформации малы, то ими можно пренебречь и рассматривать уп­ругие деформации, что мы и будем де­лать.

В теории упругости доказывается, что все виды деформаций (растяжение или сжатие, сдвиг, изгиб, кручение) могут быть сведены к одновременно происходя­щим деформациям растяжения или сжа­тия и сдвига.

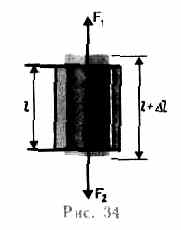
Рассмотрим однородный стержень длиной l и площадью поперечного сечения S (рис. 34), к концам которого приложены направленные вдоль его оси силы f ₁ и F ₂ (F ₁ =F ₂ =F), в результате чего длина стер­жня меняется на величину D l. Естествен­но, что при растяжении D l положительно, а при сжатии — отрицательно.

Сила, действующая на единицу пло­щади поперечного сечения, называется на­пряжением:

s=F/S. (21.1)

Если сила направлена по нормали к по­верхности, напряжение называется нор­мальным, если же по касательной к по­верхности — тангенциальным.

Количественной мерой, характеризую­щей степень деформации, испытываемой телом, является его относительная дефор­мация. Так, относительное изменение дли­ны стержня (продольная деформация)

e=D l / l, (21.2) относительное поперечное растяжение

(сжатие)

e' = Dd/d, где d -— диаметр стержня.

Деформации e и e ' всегда имеют раз­ные знаки (при растяжении D l положи­тельно, a Ad отрицательно, при сжатии D l отрицательно, a Ad положительно). Из опыта вытекает взаимосвязь e и e':

e'=-me,

где m — положительный коэффициент, за­висящий от свойств материала, называе­мый коэффициентом Пуассона.

Английский физик Р. Гук (1635— 1703) экспериментально установил, что для малых деформаций относительное уд­линение e и напряжение s прямо про­порциональны друг другу:

s = Ee, (21.3)

где коэффициент пропорциональности Е называется модулем Юнга. Из вы­ражения (21.3) видно, что модуль Юнга определяется напряжением, вызывающим относительное удлинение, равное единице. Из формул (21.2), (21.3) и (21.1) вы­текает, что

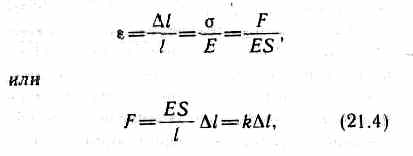
где k — коэффициент упругости. Выраже­ние (21.4) также задает закон Гука, со­гласно которому удлинение стержня при упругой деформации пропорционально действующей на стержень силе.

Деформации твердых тел подчиняются закону Гука до известного предела. Связь между деформацией и напряжением пред­ставляется в виде диаграммы напряже­ний, которую мы качественно рассмотрим для металлического образца (рис. 35). Из рисунка видно, что линейная зависимость s (e), установленная Гуком, выполняется

 

 

лишь в очень узких пределах до так на­зываемого предела пропорциональности (s_п). При дальнейшем увеличении напря­жения деформация еще упругая (хотя за­висимость s (e) уже не линейна) и до пре­дела упругости (s_у) остаточные деформа­ции не возникают. За пределом упругости в теле возникают остаточные деформации и график, описывающий возвращение тела в первоначальное состояние после прекра­щения действия силы, изобразится не кри­вой ВО, а параллельной ей — CF. Напря­жение, при котором появляется заметная остаточная деформация (~=0,2 %), назы­вается пределом текучести (s_т) — точка С на кривой. В области CD деформация возрастает без увеличения напряжения, т. е. тело как бы «течет». Эта область называется областью текучести (или об­ластью пластических деформаций). Мате­риалы, для которых область текучести значительна, называются вязкими, для ко­торых же она практически отсутствует — хрупкими. При дальнейшем растяжении (за точку D) происходит разрушение тела. Максимальное напряжение, возникающее в теле до разрушения, называется преде­лом прочности (s_p).

Диаграмма напряжений для реальных твердых тел зависит от различных факто­ров. Одно и то же твердое тело может при кратковременном действии сил проявлять себя как хрупкое, а при длительных, но слабых силах является текучим.

Вычислим потенциальную энергию упругорастянутого (сжатого) стержня, кото­рая равна работе, совершаемой внешними силами при деформации:

где х — абсолютное удлинение стержня, изменяющееся в процессе деформации от 0 до D l. Согласно закону Гука (21.4), F=kx=ESx/l. Поэтому

т. е. потенциальная энергия упругорастянутого стержня пропорциональна квадра­ту деформации (D l)².

Деформацию сдвига проще всего осу­ществить, если взять брусок, имеющий форму прямоугольного параллелепипеда, и приложить к нему силу F_tau (рис.36), касательную к его поверхности (нижняя часть бруска закреплена неподвижно). Относительная деформация сдвига опре­деляется из формулы

tgg = Ds/h,

где Ds — абсолютный сдвиг параллельных слоев тела относительно друг друга; h — расстояние между слоями (для малых уг­лов tgg»g).

 

 

Контрольные вопросы

• Что такое момент инерции тела?

• Какова роль момента инерции во вращательном движении?

• Какова формула для кинетической энергии тела, вращающегося вокруг неподвижной оси, и как

ее вывести?

• Что называется моментом силы относительно неподвижной точки? относительно неподвижной

оси? Как определяется направление момента силы?

• Выведите и сформулируйте уравнение динамики вращательного движения твердого тела.

• Что такое момент импульса материальной точки? твердого тела? Как определяется направле­ние момента импульса?

• В чем заключается физическая сущность закона сохранения момента импульса? В каких систе­мах он выполняется? Приведите примеры.

• Каким свойством симметрии пространства обусловливается справедливость закона сохранения момента импульса?

• Сопоставьте основные уравнения динамики поступательного и вращательного движений, прокомментировав их аналогию.

• Что такое свободные оси (главные оси инерции)? Какие из них являются устойчивыми?

• Что такое гироскоп? Каковы его основные свойства?

• Сформулируйте закон Гука. Когда он справедлив?

• Дайте объяснение качественной диаграммы напряжений s(e). Что такое пределы пропорцио­нальности, упругости и прочности?

• Каков физический смысл модуля Юнга?

Задачи

4.1. С одного уровня наклонной плоскости одновременно начинают скатываться без скольжения сплошные цилиндр и шар одинаковых масс и одинаковых радиусов. Определить: 1) отноше­ние скоростей цилиндра и шара на данном уровне; 2} их отношение в данный момент време­ни. [1) 14/15; 2) 14/15]

4.2. К ободу однородного сплошного диска радиусом R = 0,5 м приложена постоянная касатель­ная сила F=100 H. При вращении диска на него действует момент сил трения М = 2Н•м. Определить массу т диска, если известно, что его угловое ускорение к постоянно и равно 12 рад/с². [32 кг]

4.3. Через неподвижный блок в виде однородного сплошного цилиндра массой m= 1 кг перекину­та невесомая нить, к концам которой прикреплены тела массами m ₁=1 кг и m ₂ = 2кг. Прене­брегая трением в оси блока, определить: 1) ускорение грузов; 2) отношения T ₂/ T ₁сил на­тяжения нити. [ 1) 2,8 м/с²; 2) 1,11 ]

4.4. Скорость вращения колеса, момент инерции которого 2 кг•м², вращающегося при торможении равнозамедленно, за время t=1 мин уменьшилась от n₁=300 об/мин до n₂=180 об/мин. Определить: 1) угловое ускорение e колеса; 2) момент М силы торможения; 3) работу силы торможения. [1) 0,21 рад/с²; 2) 0,42 Н•м; 3) 630 Дж ]

4.5. Человек массой m = 80 кг, стоящий на краю горизонтальной платформы массой М = 100 кг, вращающейся по инерции вокруг неподвижной вертикальной оси с частотой n₁ = 10 мин^-1, переходит к ее центру. Считая платформу круглым однородным диском, а человека — точеч­ной массой, определить, с какой частотой n₂ будет тогда вращаться платформа. [26 мин^-1 ]

4.6. Определить относительное удлинение алюминиевого стержня, если при его растяжении затрачена работа 621 Дж. Длина стержня 2 м, площадь поперечного сечения 1 мм², модуль Юнга для алюминия E = 69 ГПа. { D l/l =Ö[2A/(ES l)]=0,03}