Если в рассматриваемом положении механизма усилие Р направлено против оси X, то подставляем его величину со знаком “–”

Реакция со стороны направляющих на ползун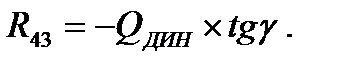

R₄₃= = н.

Так как внешние силы и инерционные нагрузки, приложенные к шатуну и кривошипу, не учитываются .

 

В проекциях на оси X,Y системы координат

.

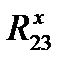⁼ н. = = н.

 

Уравновешивающий момент на валу кривошипа

.

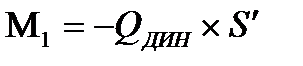М₁= = Нм.

Знак “+” в результатах означает, что — движущий момент, знак “–” - момент сопротивления.

Результаты расчётов представлены в табл.2 и на рис.5,6,7.

В положении механизма 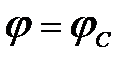строим проверочный план сил для ползуна (рис. 8). Должно выполняться условие равновесия сил:

.

 

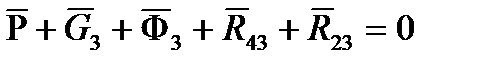
Табл.2

 

 

φ град.	Рсопр. Н	QДИН. Н	R43 Н	R41x Н	R41y Н	М1 Нм

 

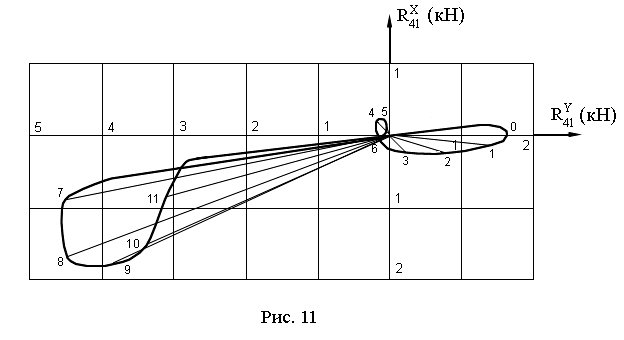
Рис.5

Рис.6

Рис.7

Рис.8

 

 

 

3 .Выравнивание хода машины. Расчёт маховика.

В качестве динамической модели машины принято вращающееся звено 1 (кривошип), являющееся ведущим звеном исполнительного механизма. Положение его определяется углом поворота φ, а движение – угловой скоростью ω ₁. При этом все силы, действующие на звенья машины, заменяются приведенным моментом М_пр, а массы и моменты инерции всех звеньев заменяются приведенным моментом инерции J_пр.

Величина приведенного момента М_пр находится из условия равенства мощностей приводимых сил и мощности на звене приведения.

Приведенный момент инерции J_пр определяется из условия равенства кинетических энергий приводимых звеньев и звена приведения.

 

3.1 Расчёт работы сил сопротивления, движущей и избыточной работ.

Приведённый момент М_с от силы сопротивления Р на ползуне (с учётом его силы тяжести G₃) находится по зависимости

М_с = (Р + G₃ cos β) ∙ S′.

 

Зависимость силы Р от угла поворота кривошипа задана графиком, приводимым в задании. Знак силы Р определяется её направлением относительно оси X. Само направление силы сопротивления противоположно скорости ползуна. Значения Р, S′ подставляются с учётом знаков.

Расположение механизма определяется углом β между положительным направлением оси X и вектором силы тяжести (угол отсчитывается от оси X против часовой стрелки).

Для вертикальной схемы (ось Х- вверх) - 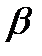=180^○,

 

В нашем задании 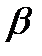= ⁰.

 

Пример расчёта: М_с= = Нм.

 

Величины М_с для каждого положения приведены в табл.3 и показаны на графике (рис.10).

 

Зная в каждом положении величину момента Мс, можно на каждом участке определить работу сил сопротивления и сил тяжести.

А_С = 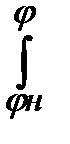М_сdφ.

 

Используем метод численного интегрирования.

Суть метода состоит в то, что работу на графике моментов, представляющую собой площадь криволинейной трапеции, образованной кривой графика (рис.9) и осью φ, приближённо, можно заменить площадью обычной трапеции:

А_C ≈ 0,5∙ (М_а + М_в) ∙ Δφ.

Здесь - (в радианах).

 

 

Рис.9

Точность интегрирования зависит от числа выбранного числа участков. Погрешность вычислений представляет собой (рис.9) площадь (заштрихована) между кривой графика момента и хордой, соединяющей начальную и конечную точки участка.

В данной работе расчёт ведётся для 12 участков.

При этом Δφ = (2π / 12) = 0,5236.

На участке от начального положения до первого

А _{0 - 1} = 0,5(М ₀ + М ₁) ∙Δφ.

А _{0 - 1} = = Нм.

На участке от начального положения до второго

А _{0 - 2} = А _{0 - 1} + А_1-2 = А _{0 - 1} + 0,5(М ₁ + М ₂) ∙Δφ.

А _{0 - 2} = = Нм.

И так далее…

Работа сил сопротивления за период будет равна

= А _{0 - 11}+0,5(М₁₁+М₁₂) ∙ Δφ.

= = Нм.

При установившемся движении за период работа движущих сил

= - .

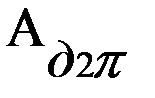Принимаем, приближённо, что М_Д=const. Тогда его величина определяется по формуле

М_д = (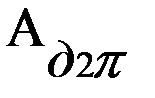) / 2π = = Нм.

Линия, соответствующая М_Д, показана на рис.10.

 

Величина движущей работы в каждом положении агрегата равна:

 

А _д =М_Д*φ (φ- в радианах). А _д = = Нм.

 

В каждом положении находится избыточная работа А_И и равное ей приращение кинетической энергии Т агрегата.

Т = А_и = М_д · φ + А_с.

Здесь 0 ≤ φ ≤ 2π, Δφ = (2π /12) = 0,5236.

Т = А_и = = Нм.

 

 

Результаты расчётов представляются на рис.11 и приводятся в табл.3.

 

 

Рис.10

 

 

 

 

Рис.11

 

 

Ориентировочная мощность двигателя (в ваттах) определяется по формуле: N = M_д ∙ ω₁ ∕ η

Здесь ω₁ = π ∙ n₁ / 30.

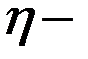общий коэффициент полезного действия, учитывающий потери на трение в кинематических парах, в ременной и зубчатой передачах.

Принимаем приближённо η = 0,85.

N= = Вт.

По найденной мощности выбираем (м.у. /3/) тип электродвигателя.

Номинальная мощность N_n= кВт.

Номинальная частота вращения n_n= об/мин.

Момент инерции ротора J_р= кг.м².

Определяем передаточное отношение от двигателя до кривошипа

i_дк = n_n / n₁ = =.

 

3.2 Расчёт изменения кинетической энергии агрегата.

Изменение кинетической энергии агрегата, равное избыточной работе, определяется по зависимости:

Т = Т_С + Т_V.

Тc - изменение кинетической энергии вращающихся масс;

Т_V- изменение кинетической энергии масс, совершающих сложно-плоское и возвратно-поступательное движения.

При малых колебаниях угловой скорости можно приближённо принять

Т_v ≈ 0,5 • (J_v - J_vн).

 

Величину J_v приведённого момента инерции масс, совершающих поступательное движение, в каждом положении вычисляется по формуле J_v = m₃ ∙ (S¢)².

Следовательно: Т_v ≈ 0,5 * * m₃ ∙ (S¢)².

Т_v = = Нм.

 

Отсюда находится в каждом положении механизма приращение кинетической энергии вращающихся масс:

Т_C = Т - Т_V.

 

Т_C= = Нм.

Величина Т_C, периодически меняясь, достигает в каких-то положениях максимальных и минимальных значений. Соответственно, в этих положениях угловая скорость будет достигать также значений ω_max и ω_min. Наибольший перепад кинетических энергий вращающихся масс будет

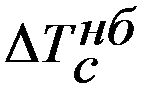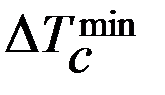= - = = Нм.

Результаты расчётов Т=А_ИЗБ., Т_c, Т_v представлены на рис.12 и приводятся в табл.3.

 

 

 

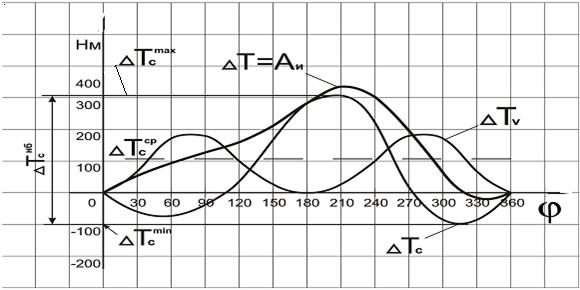
Рис.12

 

 

3.3 Определение размеров маховика.

Определяем необходимую величину J_с приведённого момента инерции вращающихся масс.

 

J_c = 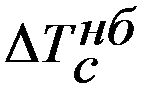/ (δ ∙ ) = = кг.м².

Величина J_со , имеющихся вращающихся масс J_со = J_п + J_р ∙ (i_дк)².

Здесь: J_п –момент инерции передаточного механизма, приведённый к валу кривошипа (задаётся в работе);

J_р ∙ (i_дк)²- момент инерции ротора двигателя, приведённый к валу кривошипа.

 

J_со= = кг.м².

 

Момент инерции маховика находится как разница между необходимой величиной J_с приведённого момента инерции вращающихся масс и величина J_со , имеющихся вращающихся масс.

 

J_М = J_c – J_co = = кг.м².

 

Конструктивно маховик выполняется в виде колеса с массивным ободом прямоугольного сечения. Расчетная схема для определения размеров обода показана на рис.13.

 

 

Рис.13

 

Принимаем,приближенно, что 90% момента инерции маховика относится к ободу. Задаём ориентировочно значение среднего радиуса R_ср= 4*ОА. Тогда масса обода находим по формуле m_об = 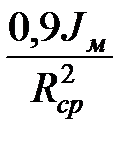= = кг.

Площадь сечения обода определим по формуле

b ∙ h = = = м².

где r - плотность материала (для чугуна r = 7200 кг/м³). Для определения размеров сечения b и h задаём соотношение b / h = 1.

 

b =h= = м.

 

Чтобы исключить возможность разрушения обода маховика под действием центробежных сил инерции, производим проверка окружной скорости

V_окр = w_ср (R_ср +0,5h) ≤ V_КР. Для чугуна V_КР = 30м/c.

V_окр= = ≤ V_КР.

По уточнённым данным вычерчиваем в масштабе эскиз маховика (рис.14), на котором проставляем наружный диаметр d_Н = (2R_СР + h), внутренний диаметр обода d_ВН = (2R_СР - h) и ширина обода b.

При этом численные значения этих величин округляем до ближайших стандартных из ряда нормальных линейных размеров. Все остальные элементы маховика оформляем из конструктивных соображений, их размеры не проставляем.

d_Н = = м.

d_ВН= = м.

b= м.

 

Рис.14

 

3.4 Контрольный анализ хода машины.

Анализ хода выполняется для проверки расчёта маховика и включает в себя определение мгновенных значений угловой скорости кривошипа, определение коэффициента неравномерности хода и сравнение его с заданным. Отклонение Δω угловой скорости от её среднего значения, определяем по формулам:

Δω = ( Т_С - 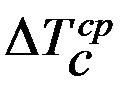) / (ω_ср ∙ J_C),

где 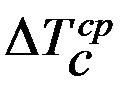- приращение кинетической энергии в положении, где ω=ω_ср.

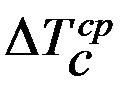=0,5( + )= = Нм.

 

Δω= = с^-1.

 

Так как при наличии маховика колебания скорости малы, на графике угловой скорости откладываем её отклонения Δω от среднего значения (рис.15).

 

 

Контрольный коэффициент неравномерности хода δ_К определяем по формуле δ_к = (Δω_нб) / ω_ср, где Δω_нб = (ω_max - ω_min) – определяются из расчётов (табл.3 и рис.15). Отклонение оценивается в процентном отношении к заданному (Δδ)% = 100(δ_к - δ) / δ.

 

Δω_нб= = 1/с.

 

δ_к= =.

 

(Δδ)%= =.

 

 

Рис.15

 

 

Литература

1. Фролов К.В.Теория механизмов и механика машин–М.:Высш.шк.2005.

2. Кинематический и силовой расчет механизма. Метод. указания к выполнению курсовой работы

по ТММ. Изд. Кафедры ТМ и ДМ. – СПб.: ПИМаш, 2011.

3. Выравнивание хода машины. Расчёт маховика. Метод. указания к выполнению курсовой работы по ТММ. Изд. Кафедры ТМ и ДМ. – СПб.: ПИМаш, 2009.

 

φ град.

РС Н

МС Нм

АС Нм

АД Нм

АИ Нм

ΔТV Нм

ΔTC Нм

Δω 1/с

Ω 1/с

Табл.3