Грек математикасының Римдік дәуірі

1. Математикадағы жаңа бет бұрыс

2. Геронның практикалық геометриясы

3. Гректердің тригонометриясы, Менелай және Птолемей

4. Диофанттың алгебрасы

5. Грек математикасының ақыры.

1. Мың жылға созылған грек математикасы тарихындағы ақырғы ақырғы кезең Рим империясының құрылу, орнығу, қирау дәуірімен байланысты. Римдіктер бүкіл Орта теңіз алқабын, оның Грецияны қоса барлық негізгі эллиндік елдерін басып алып, үлкен империя құрады. Рим б.з.д 212ж. Сиракузды, 146ж Карфагенді, 146ж. Грецияны, 64ж. Месопотомияны бағындырады. Олардың Птоломейлік Египетті жаулауы б.з.д 30-жылдары аяқталды.

Біздің жыл санауымызға дейінгі екінші ғасырда басталған эллиндік ғылымның біртіндеп кері кетуі бұл тұста бүтіндей тоқырауға ұласады. Мұның негізгі себебі римдіктерді ұзаққа созылған жауынгершілік соғыстардың салдары еді. Осының тікелей әсерінен римдіктерге бағанған эллимдік елдердің, экономикалық және мәдени елдердің өмірі күрт төмендеп, дағдарысқа ұшырайды. Гректердің шығармашылық ақыл-ойы бұрынғы дәреже-беделінен айырылады,оның тұрмыс тауқыметінен зардап шегіп, әбден қажыған халықтың көңіл күйіне сай келетін діни – мистикалық ілім сымақтар өріс алады. Математика тәрізді абстракты ғылымдар жұртты қызықтырудан қалады.

Тек б.з. бас кезінде Рим империясы біржола орнығып, саяси экономикалық жағдай қайта түзеле бастағаннан кейін грек ғылымы біртіндеп жандана бастайды. Ғылым орталығы әліде болса баяғы Александрия халықаралық ғылыми тіл грек тілі болып қала береді. Рим бұл жөнінде онымен бәсекелесуге жарамайды. Католиктік діни тіл-латын тілі кейін барып қана халықаралық ғылыми тіл болып жарияланды. Осыдан былай ғылым, математика тарихындағы Александрия дәуірінің екінші кезеңі басталады.

Әрине, римдіктер грек мәдениетінен бүтіндей бас тартпады. Рим ежелгі гректердің шешендік өнерін (риторика, люриспруденция, поэзия) кқркемдік өнерін қабылдап өркендетеді. Ал математика болса практикалық арифметика, жер өлшеу мәселелерінен аспады.

Сөйтіп, грек ғылымы сүрініп барып, құламай қайта тұрып кетеді. Бірақ заман ағымы, бой көрсетіп келе жатқан жаңа өндіріс қатынастары практика талабының және басқа объективтік факторлар бұрынғы эллиндік, классикалық бағыттан бұрылып, мақсатқа қарай бет алады. Бұл өзгеріс математикада да өз көрінісін танытады.

Шынында, б.з. І-ІІ ғ.ғ математика даму тарихында біраз жандану, өрлеу, жаңа бет бұрыс кезеңі орын алады. Бұл уақытқа дейін грек математиктерінің зерттеулері негізінен тек теориялық геометрияға бағындарылып келсе, енді математиканың қоғамдық өндіріске жақын, практикада қолданыс табатын салаларын өркендету қолға алына бастады.

Ежелгі Мысыр, Вавилон т.б елдердегі жалаң практикалық, догматикалық математикадан гректердің қолданба математикасының басты бір өзгешелігі– мұнда жалаң теорияларға емес, керісінше, практикалық формулалар мен ережелерге сүйенеді. Ал бұл болса, логикалық, дедуктивті түрде дәлелденеді. Мәселен, жаңа практикалық бағыттағы математикалық ізденістердің дұрыс – бұрысы Евклид, Архимед т.б математика теоретиктерінің қағидалары арқылы сыналып, тексеріліп отырады.

Дамудың жаңа бағытындағы бұл математикалық зерттеулерде ең әуелі есептеу, өлшеу әдістерін жетілдіруге барынша назар аударылады; жазық және сфералық тригонометрияның негіздері қаланады; геометрияға емес арифметикаға арқа сүйеген қазіргі мағынадағы алгебралық әдістері дамытылады; Пифагор, Евклид, Архимед, Аполлоний тәріздес математика кемеңгерлерінің еңбектерін өңдеу, түсіндіру(комментировать), жақсарту мәселесіне көп көңіл бөлінеді; математиканың өткен тарихына шолу жасау әрекеті басталады.

Бұл беталыстың ғылым тарихында маңызы үлкен болды. Ол кейіннен бүкіл математиканы өзгертуге, әріппен өрнектеуге негізделген қазіргі символикалық математикалық есептеулердің тууына бастама жасады. Жаңа бағытта жемісті жұмыс істеп, ғылым тарихына өшпес із тастаған осы тұстағы көрнекті математиктердің негізгі жетістіктеріне тоқталайық.

2. Алексанриялық Герон қай-қайсымызға мектеп математикасынан белгілі, атақты «Герон формуласының» авторы. Ол б.з І ғасырда өмір сүрген көрнекті энциклопедист математик. Герон Александрияда ұстаздық қызмет атқарған. Ол математикамен қатар физика, астрономия, механикамен көп шұғылданған.Сондықтан замандастары оны «Герон – механик» деп те атаған. Герон сығылған ауа және будың күшімен қозғалысқа келетін сан алуан тамаша механизмдер мен практикалық өлшеу аспаптарын жасаған. Геронның «Диоптрика», «Пневматика» атты шығармалары осыларға арналған. Герон өз еңектерін инженирлер, архитекторлар мен әр түрлі қолөнершілерге арнап жазған. Ол есептеу математикасы бойынша бірсыпыра жетістіктерге жетеді; геометриялық алгебра жәрдемімен шешілетін есептерге сандық мән беріп, оны практика мұқтаждығына лайықтаған. Математикалық таза теориялық мәселелер бойынша Евклидтің «Бастамаларына» түсініктеме жазып қалдырған.

Геронның математикалық шығармалары негізінен ежелгі практикалық математиканың энциклопедиясы болып табылады. Мұнда математиканың қолданылуы Евклидтің, Архимедтің т.б ғалымдардың зерттеулеріндегі сияқты күңгірттенбей, айқын да анық сипатта көрінеді.

Бізде Геронның «Метрика», «Геометрия» деп аталатын трактаттары келіп жетті. «Метрика» – өлшеулер туралы ілім – үш кітаптан тұрады. Бірінші кітапты аудандар мен беттерді өлшеу ережелері келтірілген. Мұнда әр түрлі қабырғалы үшбұрыштың ауданын табуға арналған Герон формуласы:

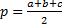, берілген. Герон бұл формуланы үшбұрышқа іштей сызылған дөңгелек арқылы дәлелдейді. Араб жазбаларында «бұл формуланың Героннан көп бұрын Архимедке мәлім болғаны жайында дерек бар.

Герон бұл формуланы қолданудың сандық мысалдарымен түсіндіреді. Бұл тұрғыда айта кететін бір жайт, ол тек бүтін рационал сандармен ғана шектелмей түбір астындағы иррационал сандарды да қарастырады. Мына бір мысал есепті қарастырайық:

«Үшбұрышты сен былай өлшейсің. Мысалы, үшбұрыштың қабырғаларының ұзындықтары 13, 14 және 15 өлшем жіп болсын. Ауданды табу үшін сен былай істе, 13, 14және 15-ті өзара қос, 42 шығады. Мұның жартысы 21 болады. Бұдан үш қабырғаны біртіндеп ал; ең әуелі 13-ті ал, сонда 8 қалады, сонан соң 14-ті ал, 7 қалады; ең соңынан 15-ті алсаң, 6 қалады. Енді бұларды өзара көбейт, 21-ді 8-ге көбейтсең, 168 болады, мұны 7-ге көбейтсең, 1176 шығады; ал мұны 6-ға көбейтсең, 7056 шығады. Мұның квадрат түбірі 84 болады. Міне үшбұрыштың ауданы осынша өлшем жіп болады.

Герон бұл шығармасында квадрат түбірді жуықтап табудың вавилондық әдісін, мысырлықтардың бөлшекті жазу жіне ережелерді баяндау тәсілдерін келтіреді. Осымен қатар, ол жуық куб түбірді табу жолдарын көрсетеді. Радиусы r дөңгелекке іштей сызылған дұрыс жеті бұрыштың қабырғасын Герон жуықтап
деп алады және a жуық түрде дөңгелек центрінен оған іштей сызылған дұрыс алты бұрыштың қабырғасының қашықтығына, яғни болатынын табады. Герон π саны үшін Архимед тапқан мәнін алады. Геронның бұл еңбегінде дұрыс емес жазық фигуралардың, беттердің аудандарын жіне әр түрлі көлем табу әдістері және басқа бірсыпыра практикалық геометрия мәселелері қамтылған.
Геронның екінші шығармасы - «Геометрияның» да мазмұны «Метрикаға» ұқсайды. Мұндағы негізгі бір өзгешелік ережелер мен формулалар дәлелденбейді, тіпті айрықша тұжырымдалмай,бірден мысалдар шығаруға көшеді. Мысыр математикасындағы сияқты мұнда да бір типті бірнеше сан мысалдары келтіріліп, олардан жалпы қорытынды шығару оқушылардың өздеріне тапсырылады.

«Геометрияда» квадрат теңдеулер, анықталмаған теңдеулер қарастырылады. Мұнда мысалы, екіншісінің периметрі біріншісінің үш еселенген периметріне, ал біріншісінің ауданы екіншісінің ауданына тең болатындай екі тік тікбұрышты табу немесе рационал қабырғалы және ауданы берілген тік бұрышты үшбұрыш табу деген сияқты есептер беріледі.

Геронның «Стереометрия» деп аталатын шығармасында геометриялық денелердің көлемдерінен басқа үйдің, театрдың, амфитеатрдың, кеменің, құдықтың, шарап бөшкесінің, т.б көлемдерін табу қарастырылады. «Геометрияның» бір бөлігі болып саналатын «Геодезия» атты трактатында Герон үшбұрыштарды өлшеуді өз алдына бөліп баяндайды.

3. «Тригонометрия» деген сөз грекше «үшбұрыштарды өлшеу» дегенді білдіреді.(«Тригоном»-үшбұрыш және «метро»-өлшеймін).Тригонометрия астрономия мен география ғылымдарының дамуына тікелей байланысты туып, қалыптасқан. Тригонометрияның кейбір бастамалары, элементтері ежелгі Вавилонда кездеседі. Алайда гректер тригонометрияны астрономияның бір бөлігі ретінде қараған. Мұнда ең әуелі шар бетінде орналасқан үшбұрыштарды шешуге негізделген сфералық тригонометрия дамытылған.Ондай сфералық бұрыштардың қабырғалары шар бетіндегі үлкен дөңгелектердің доғалары болып келеді.

Ежелгі грек оқымыстылары ең алдымен тік бұрышты үшбұрыштарды (жазық немесе сфералық) шешеу мәселесін, яғни берілген үш элементі бойынша үшбұрыштың басқа элементтерін анықтау мәселесін қояды. Тригонометриялық мазмұндағы алғашқы зерттеулер Евдокстан басталған болу керек. Алайда гректер тригонометриясы туралы толық та жүйелі мағлұматты біз Менелай мен Птолемей еңбектерінен табамыз.

Александриялық Менелай - б.з І ғасырында өмір сүрген астроном және математик. Ол «Сферика» деп аталатын үшбұрыштар жөніндегі үш томдық көлемді еңбектің авторы. «Сфериканың» грекше нұсқасы бізге жетпегенмен ол араб аудармасы арқылы сақталған. Менелайдың сонымен қатар «Геометрия элементтері», «Үшбұрыштар туралы кітап» деп аталатын геометриялық трактаттар жазған көрінеді.

«Сфериканың» бірінші кітабында Евклидтің «Бастамалары» үлгісінде сфералық тік бұрышты үшбұрыштар туралы теоремалар дәлелденеді. Мұнда ұқсастығы жоқ сөйлемдер де кездеседі. Ол, мәселен, сфералық үшбұрыштардың ішкі бұрыштарының қосындысы екі тік бұрыштан үлкен болатынын дәлелдейді. Сфералық геометрия –математика тарихындағы ең бірінші евклидтік емес (биевклидті) геометрия жүйесі болып табылады.

«Сфериканың» екінші кітабының мазмұны жоғарыда айтылған Теодосийдің шығармасының мазмұнымен бірдей. Бірақ дәлелдері қысқа да анық болып келеді.

«Сфериканың» үшінші кітабы негізінен тригонометрия мәселелеріне арналған. Әрине, гректерде ол кезде қазіргі мағынадағы тригонометрия жоқ болатын, синус және басқа тригонометриялық функциялар анықталмайтын, синус сызығының орнына хордалар жүретін, қазірше айтсақ: α бұрышының синусы 2α бұрышын керіп тұрған хорданың жартысы болады.

Бұл кітапта кейін арабтар қималар теоремасы немесе алты шама туралы ереже деп атап кеткен атақты Менелай теоремасы дәлелденеді. Мұнда жазықтықта немесе сферада әрқайсысы қалғандарын үш нүктеде қиып өтетін төрт түзу немесе сәйкес үлкен дөңгелек доғаларынан құралған фигураның қасиеті тұжырымдалады. Бұл теореманы орта ғасырларда «қималар фигурасы» деп атаған, қазір мұны толық төртқабырғалық немесе трансверсаль деп атайды.

Жазықтық жағдайында (8-сурет) Менелай теоремасы ежелгі математика көп қолданған құранды қатыстар ілім терминдері бойынша былай жазылады: (1) немесе (2). Ал сфера жағдайында (1) теңдіктегі кесінділер екі еселенген қабырғалардың хордаларымен немесе қазіргі таңбалау бойынша, қабырғалардың синустарымен алмастырылады.

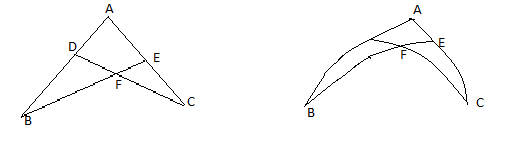
8-сурет

Толық төртқабырғалықты ACD, ABE, ECF және DBF төрт үшбұрыштың кез келгенінің BFE, CFD, BDA және CEA қиюшы транверсальдарымен сәйкес қиылысуынан пайда болған фигура деп те қарауға болады.Сондықтан Менелай теоремасын төрт түрлі вариантта жазуға болады. «Сферикада» бірінші және үшінші варианттары келтірілген, қалғандары оларға симметриялы болады:

Менелай теоремасы әртүрлі жазық және сфералық үшбұрыштарды шешуге қолданылған.

Клавдий Птоломей - ежелгі дүниенің ең ұлы астрономы. Птолемейдің б.з 120жылынан бастап Александрияда өмір сүргені ғана мәлім. Ол - астрономия жөнінде жазылған, арабтар кейіннен «Алмагест» деген үлкен еңбектің авторы. Птолемей әлем жайлы геоцентрлік жүйені жасаушы. Бұл жүйе бойынша Күн, Ай және басқа аспан шырақтары әлем центрі Жерді айнала шеңбер бойымен қозғалыста болады.

Птолемейдің «Алмагесті» 13 кітаптан тұрады. Тригонометрия мәселелері І-ші кітапта келтірілген. Мұнда Птоломей өзінен бұрынғы Менелайдың зерттеулеріне сүйенгені байқалады. Птоломей дөңгелек шеңберін 360градусөа, ал оның диаметрін 120 бөлікке бөледі. Сөйтіп, хорданың ұзындығын дөңгелектің радиусы арқылы өрнектейді. Түрлі бұрыштарға қандай хордалар сәйкес келетінін анықтау үшін Птоломей шеңберге іштей сызылған төртбұрыш туралы теореманы дәлелдейді. Бұл теорема бойынша, егер тұртбұрыш дөңгелекке іштей сызылса, онда оның диогоналдарының көбейтіндісі қарама-қарсы қабырғалардың көбейтінділерінің қосындысына тең болады. Бұл теорема қазір Птоломейдің есімімен аталып жүр.

«Егер төртбұрыш тең қабырғалы болса, онда дәлелдеу оп-оңай. Әр түрлі қабырғалары төртбұрыш, мысалы, ABCD дөңгелекке іштей сызылған дейік. (9-сурет); диогоналдарын жүргіземіз. ABD бұрышы DBC бұрышынан үлкен болсын, онда біріншісі керіп тұрған AD доғасы бұл төртбұрышта үлкен болады. DBC бұрышына тең ABЕ бұрышын саламыз. ВАЕ және ВDС бұрыштары бір доғаға тірелетін болғандықтан, олар тең болады. Сондықтан, ABЕ және DBC үшбұрыштары ұқсас болады және АВ-нің СD-ға көбейтіндісі DB-нің АЕ-ге көбейтіндісіне тең болады.

9-сурет 10-сурет

ABD бұрышы ЕВС бұрышына тең және ВСЕ, АDВ бұрыштары өзара тең болғандықтан, СВЕ және АВD үшбұрыштары ұқсас. Ендеше, ВС-ның АD-ға көбейтіндісі ДВ-нің СЕ-ге көбейтіндісіне тең. Олай болса, ВС-нің DА-ға және АВ-нің СD-ге көбейтінділерінің қосындысы ВD-нің СЕ-ге және ВD-ның АЕ-ге қосындысы, яғни ВD-нің СА-ға көбейтіндісіне тең болады. Біздің дәлелдейтініміз де осы еді»

Сонымен ВD*СА= BC*DА+АВ* CD (3)

Егер диогональдардың бірі дөңгелектің диаметрі болса, онда (3) теңбе-теңдік

(4)

формуласына эквивалент болатыны оңай дәлелденеді. Шынында, егер диогональ АС дөңгелектің диаметрі 2 R және <ВАС=α, <САD=β болса (10-сурет) онда
, . ; ; .

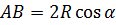Енді осы мәндерді (3) теңбе-теңдікке сәйкес қойсақ, онда (4) формула келіп шығады.

Птоломей өзінің теоремасын хордалар кестесін жасауға негіз етеді. Птоломейдің «Алмагестінде» жарты градус аралатып 0º-тан 180º-қа дейінгі хордалар кестесі келтірілген, ол 0º-тан 90º-қа дейінгі синустар кестесіне сай келеді. Ол алпыстық бөлшектерді пайдаланады.

Доғалар Хордалар

0; 31; 25

1 1; 2; 50

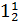1, 34; 15

 

2 2; 5; 40

2; 37; 4

3 3; 8; 28

3; 39; 52

4 4; 11; 16

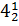4; 42; 40

5 5; 45; 27

Мысалы хорда

 

Осыдан

Тарихи жазбалар бойынша хордалар кестесін алғаш жасаушы ретінде б.з.д 2 ғасырдатөмір сүрген астроном Гиппарх болып саналады. Бірақ ол кестелер біге келіп жетпеген. Сондықтан да Птоломей кестесі- математика тарихында біз білетін тұңғыш тригонометриялық кесте. Птоломей Гиппархтың астрономиясымен жете танысып, оны өзінің «Алмагестіде» кемелдендіреді.

Птоломей «Алмагесте» астрономияға қажет көптеген әртүрлі сфералық үшбұрыштарды шешуге тиісті болады. Мұнда ол Менелай теоремасын және одан шығатын салдарларды шебер пайдаланады. Мәселен, «Алмагестің» бірінші кітабының 14-тарауында. Күн орнының берілген λ ойлық бойынша δ ауысуын былай табады. Мұнда ЕВ эклиптиканың ЕА аспан экваторына көлбеулігі ξ белгілі деп саналады. (11-сурет).Н-Күннің орны, сондықтан, FC доғасы-90º, ЕН доғасы-λ; Күннің ауысуы δ=FН доғасын табу керек. FС, ЕВ доғалары-90º.

 

11-сурет

Суреттегі қиюшылар фигурасына немесе толық төрт қабырғалықта Менелай теоремасын қолданып, мынадай қатынастар алуға болады:

Белгілі мәндерді орнына қойып, былай жазуға болады:

 

Қазіргі таңбамен жазсақ, бұл қатынас sinδ=sinλ*sinε формуласымен дәл келеді. Птоломейдің бізге «Алмагестен» басқа тригонометрияны кең қолданылған «Аналлема» және «Планисферий» деп аталатын екі шығармасы келіп жетті. Мұның екіншісінде аспан сферасының стереографикалық проекциясы баяндалады.

Птоломейдің көп томдық «Географиясында» жер бетіндегі 8000 пункттің ендігі мен бойлығы көрсетіледі. Бұл еңбекте жер бетіндегі кез келген нүктенің орнын екі сан арқылы анықтау жөнінде координаттар идеясы бар.

Птоломей математика тарихында ең бірінші болып жоғарыда келтірілген Евклидтің параллель түзулер жайлы бесінші постулатын дәлелдеуге тырысады. Бірақ оның дәлелінде де кейін көптеген математиктерде орын алған логикалық қате бар еді. Олар бесінші постулатты дәлелдеу үшін ашық немесе астыртын түрде оған пара-пар болатын басқа қорытындыға сүйенеді. Бұл логикалық қайшылық, сондықтан мұндай дәлелдеу дұрыс болмайды.

4. Грек математикасындағы б.з I - II ғасырларында басталған бетбұрыс, жаңа қарқын III ғасырдың ортасында өзінің шарықтау шегіне жетеді.Бұл самғау ежелгі дүниенің ең соңғы ұлы математигі Диофанттың математикалық шығармашылығынан көрінеді.

Диофант б.з 250 жылдары Александрияда өмір сүрген. Тек қана VI ғасырда грамматик Метродор антологиясында оның қанша жасағаны туралы бір жұмбақ есеп бар. қабірінің басына қойылған құлыптасқа осы жұмбақ есеп жазылса керек.

Диофанттың 13 кітаптан тұратын, «Арифметика» деп аталатын көлемді еңбегінің бізге алтауы ғана жеткен.Бұл еңбек түгелдей арифметика мен алгебра есептеріне арналған. Онда 180 есептің шығарылу жолы көрсетіледі. Арифметика Дионосий дейтін замандасына арнап жазылған. «Құрметті Дионосий, -деп бастайды еңбегін Диофант, -сенің сандар араласатын мәселелерді ерекше ынтамен оқып-зерттейтініңді ескеріп, мен олардың табиғаты мен құдіретін ең басынан бастап баяндап беруді мақұл көрдім».

Диофант «Арифметикасының» баяндау стилінің ежелгі грек математиктерінің канондарынан сапалы түрде екі өзгешелігі бар.Ол теңдеулердің шешудің геометриядан тыс таза арифметикалық – алгебралық әдістер арқылы жүргізеді. Екіншіден, Диофант ғылым тарихында тұңғыш рет математикалық символдар(таңбалар) тілін пайдаланды. Ол белгісіз шамалар үшін айрықша таңбалаулар енгізеді. Сондай – ақ онда азайту, қысқарту, теңдік сияқты ұғымдарды таңбалау да ұшырасады.

Диофанттың символикасы сөздерді қысқартуға негізделген. Алгебралық тарихында бұл кезең осыған дейінгі математикадағы алгебралық тәуелділіктерді сөзбен өрнектеуден(риторикалық алгебрадан) бас тартып, сол өрнектерді қысқартуға («Синкоптік» алгебра) көшу кезеңі болып табылады.Дамудың келесі сатысы қазіргі таза символикалық алгебра болды.

Диофант теңдеулерінде белгісіз сан (аритмос) коэффициенті болғанда белгісіздің таңбасынан кейін жазылады.Мысалы, аритмос – 11 .Белгісіздің дәрежелерін Диофант сәйкес грек атауларының бас әріпімен таңбалайды. - «дюнамис» т.с. Диофантта белгісіздің кері шамасы да және оның дәрежелері де таңбаланады. Қосу, көбейту, бөлу таңбалары жоқ, азайту үшін таңбасы алынған. Теңдік сөзбен немесе і әрпімен жазылады.Теңдеудің бос мүшесі үшін арнайы таңбасы алынған, ол бірлік (монес) сөзінің бас әрпі. Сандар әріптерн арқылы кескінделеді. Мысалдар келтірейік:

a) теңдеуін бейнелейді.

b) бізше +5х+2 көпмүшесін білдіреді.

Диофанттың «Арифметикасында» осындай символикамен белгіленген анықталған, анықталмаған теңдеулерге келтірілген есептердің шешуі беріледі, ал ережелер мысалдар арқылы көрсетіледі. Теңдеулердің оң бүтін және бөлшек шншулерін табуға баса назар аударылады. Шешуі теріс сан болатындай теңдеуді ол мағынасыз теңдеу деп санап, бүтіндей қарастырмайды.Диофант иррационал сандарды қолданбайды. Егер теңдеудің түбірі иррационал болып кездессе, есептің шартындағы берілгендерді іріктей отырып, жауабы рационал сандарға келетіндей етіп, есепті қайта құрады.

Анықталған теңдеуге арналған есептер сызықтық, квадрат, текмбір дербес жағдайда куб теңдеуге келеді. Диофант берілген теңдеуді канондық түрге келтіру үшін ұқсас мүшелерін топтау, теңдеудің екі жағына бірдей шамалар қосу арқылы теріс мүшені жою ережелерін көрсетеді. Ол тек бір он, түбір табумен қанағаттанады. Мысалдар келтірейік:

1. Екі санның квадраттарының қосындысына тең санды басқа екі санның квадраттарының қосындысына тең болатындай етіп жазу керек. Диофант бұл проблеманы шешуді мынадай есеппен түсіндіреді:

«Айталық берілген сан 13 болсын, ол 2 мен 3-тің квадраттарының қосындысына тең.

Бір квадрат қабырғасының ұзындығы х+2 болсын, ал екінші квадрат қабырғасының ұзындығы 2х-тен 3-і кем, яғни 2х=3 болсын. Сонда бірінші квадраттың ауданы , екіншісі болады. Екеуінің ауданын қоссақ, болады. Есептің шарты бойынша бұл 13-ке тең болуы керек:

».

Сонымен бірінші квадраттың қабырғасы , екіншісінікі . Квадраттарының аудандары: және . Бұл сандардың қосындысы 13 болады, яғни есепті қанағаттандырады.

2.Әрқайсысының квадраты екінші санмен қосылып, басқа бір санның квадраты болатындай екі сан табу керек. «Бірінші сан х, екінші сан 2х+1 болсын. Бірінші санның квадратына екінші санды қоссақ, тағы да квадрат шығады: .

Екінші санның квадратына бірінші санды қоссақ, 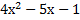шығады. Бұл да квадрат болуы керек. Осы квадраттың қабырғасы үшін 2х-2 алайық. Сонда оның квадраты болады.

теңдігінен шығады».

3.Берілген квадрат санды екі квадрат санның қосындысына жіктеу керек.

«Берілген квадрат сан 16 болсын, ал ізделініп отырған квадрат санның біреуі 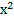, екіншісі болсын. Сонда ; бұдан ізделініп отырған квадрат сандардың біреуі , екіншісі .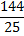

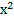Бұл есепті былай жалпылауға болар еді. Айталық, берілген сан болсын, ізделініп отырған квадрат сандардың біреуі , екіншісі болсын. Сонда

, бұдан , .

Диофант квадрат теңдеулерін жалпы шешу жолын және 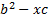өрнегі квадрат сан болған жағдайда ғана оның түбірі рацион сан болатынын білген. Диофант куб теңдеуге келетін бір-ақ мысал қарастырады. Ол теңдеуін

теңдеуіне келтіріп -, «бұдан х-тің 4-ке тең болатыны шығады» дейді, бірақ оның қалай табылғанын айтпайды.

Диофанттың математикаға қосқан негізгі жаңалығы –оның анықталмаған теңдеулерді шешу әдістерін табуы. Ол 50-ден астам әртүрлі кластарга жататын шамамен 130 аныкталмаган теңдеулердің рационал шешуін көрсетеді.Анықталмаған теңдеулерді қазір диофант теңдеулері деп те атайды.Ол әрбір теңдеудің тек бір ғана рационал шешуін анықтаумен шешіледі.Онда анықталмаған теңдеулерді жалпы шешу тәсілдері жоқ. Шыққан нәтиженің дұрыстығы дәлелденбейді,тек есеп шартын қанағаттандыруы ғана тікелей тексерілді.

Диофанттың «Арифметикасында» негізінен .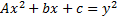

түріндегі анықталмаған теңдеулер қарастырылады. Бұл теңдеулердің ішінде қазір «Пелль теңдеулері» деп аталып жүрген және

теңдеулер де бар. Диофантта сандар теориясының екі бүтін санның көбейтіндісін екі саның квадратының қосындысына жіктеу туралы т.б.теоремалары да кездеседі.

a және b өзара жай сандар болып келген жағдайда түріндегі Диофант теңдеулерінің Жалпы теориясын XVII ғасырдағы француз математигі Баше де Мезариа (1589-1638) құрады. Ол 1621 жылы Диофанттың «Арифметикасын» грек және латын тілдерінде түсініктемелер жазып бастырып шығарады. Екінші дарежелі диофант теңдеулерінің жалпы теориясын жасау жолында П.Ферма Дж.Валлис,Л.Эйлер,Ж.Лагранж,К,Гаусс сияқты көрнекті математиктер көп еңбек сіңірді.Осының нәтижесінде, XIX ғасырдың басында екі белгісізі бар екінші дәрежесі рационал коэффициентті теңдеуін жалпы түрде шешу проблемасы қарастырылды.Диофант теңдеулері казіргі математикада да жан-жақты зерттелуде.

XVII ғасырдағы француздың ұлы математигі Ферма Диофанттың «Арифметикасын» оқып отырып,Диофанттың әлгінде ғана айтылған берілген квадрат санды екі квадраттың қосындысына жіктеу туралы есебінің тұсына былай деп қарастырган екен. «Керсінше кубты кубтардың қосындысына,биквадратты биквадраттардың қосындысына жалпы алғанда,квадраттан жоғары қандай бір дәрежені болмасын корсеткіші сондай дарежелер қосындысына жіктеуге болмайды. Мен бұған өте тамаша дәлел келтірдім,бірак оны жазып калдыруға кітаптын ашық жерінің аз болып турғаны».Басқаша айтқанда әңгіме . Диофант теңдеуінің х=у болғанда рационал шешуі болмайтынын дәлелдеу керек еді. Алайда «Ферманың үлкен теоремасы» деп аталатын бұл теорема жалпы түрде куні бүгінге дейін дәлелденген жоқ.

Диофанттың «Арифметикасы» орта ғасырларда Шығыс математиктерінің еңбектерінде алгебра ғылымының өз алдына жеке ғылым саласы болып қалыптасуына, сондай – ақ XVI – XVII ғасырларда Европада осы ғылымның дамуына үлкен ықпал етті.

5. Диофанттың «Арифметикасы» тарихта ежелгі математиканың ең соңғы көлемді де терең мағыналы шығарма болып қалды. Диофанттан кейін көптеген оқымыстылар өткен ұлы математиктер мен философтардың еңбектеріне комментарийлер жазумен көп шұғылданады. Бұлардың қатарында Папп(IIIғ), Теон(IVғ), Гипатия(IV-Vғ), Прокл(Vғ), Симпликий(Vғ), Евтокий(V-VIғ) және басқалар болды.Бұл деректердің математика тарихы үшін маңызы зор. Ежелгі грек математиктерінің кейбір көп аса маңызды туындылары кейінгі ұрпаққа осы оқымыстылардың еңбектері арқылы келіп жетті. Мысалы, Хиостық Гипократтың «айшық тәріздес фигуралардың ауданын табу(квадраттау)» трактатының үзіндісі Симпликийдің осы еңбек туралы жазылған комментарийлерінің ішінен алынды. Осы сияқты кубты екі еселеу есебін математиктердің қалай шешкендері туралы мағлұматтар Папп және Евтокий комментарийлерінен табылды.

Ол комментарийлерді математиканы оқытуды, насихаттауды көздеген әдістік мұралар жиыны деп қарап, оларда қолданылған әдіс-тәсілдерді өз алдына зерттеу тарих алдындағы келесі мәселелердің бірі деп білуіміз керек. Бұл еңбектерде математика тарихының бастамасы бар. Папп комментарийлері- осылардың ішіндегі ең көлемдісі әрі көрнектісі.

Александриялық Папп III ғасырдың IV ғасырдың бас кезінде Александрияда өмір сүрген. Ол астрономиялық еңбегінде 320 жылы қазан айының 18 жұлдызында Күннің тұтылуын қалай бақылағанын жазады. Папптың негізгі шығармасы «Математикалық жиын» деп аталады.Мұнда ежелгі грек геометриясы әрі толық, әрі анық, терең білімділікпен баяндалады. Мұнда толып жатқан тарихи математикалық мағлұматтар келтіріліп, 30-ға жуық автордың аты аталады, сондықтан да ол математика тарихы жөніндегі маңызды құрал болып саналады.Папптың бұл еңбегі көлемді,сегіз бөлімнен тұрады,мұнда ол өзінен бұрынғы математиктер құрастырып кеткен басты – басты проблемаларды топтастырып баяндайды, қиын, түсінуге ауыр жерлдерін жеңілдетіп беруге көп назар аударады.

Папп тек ескіні,көне математиканы ұқсатушы,түсіндіруші ғана емес,ол өз тарапынанда математикалық зеттеулер жүргізген білімдар математик болған.Маселен ол шарға іштей сызылған дұрыс көпжақтарды қалай салу тәсілін көрсетеді. Айналу денесі туралы Папп «Гюльден теоремасы» деп аталып кеткен теореманы дәлелдейді.

IV ғасырдың аяғында өмір сүрген белгілі математиктердің бірі – Александриялық Теон. Ол Птолемейдің «Алмагестіне» 11 кітаптан тұратын түсініктеме жазған.Ірі математик болмаса да Теон мықты тарихшы және методист болған. Ол мәселен, алпыстық бөлшектерді көбейту, бөлу, олардан түбір табу әдістерін кемелдендіреді. Теонның түсініктемелерінде аса бағалы тарихи деректер бар. Ол Евклидтің «Бастамаларын» жеңіл тілмен қайта баяндап жазған. Бұл шығарма орта ғасыр заманында Евклидті оқып – үйрену туралы кең тараған оқулықтардың бірі болды.

Біздің заманымыздың IV – V ғасырларынан бастап грек математикасы сан түрлі себептерден құлдилап төмендей бастайды. Бұл себептердің ең бастысы – христиан діні тарапынан ғылым мен мәдениетке жасалған дұшпандық пен зұлымдық болды. «Бізге Христостан басқаны білудің қажеті жоқ. Інжілден басқаны оқудың қажеті жоқ.» - деген қағида христиан діншілерінің ұранына айналды. Грек білімпаздары «кәпірлер» атанып қуғынға ұшырады. Ғылыми кітапханалар жойыла бастады. Мысалы, христиан діндарлары 390ж атақты Александрия кітапханасын өртеп жіберді.

Бұған тарихқа мәлім тұңғыш әйел оқымысты, философ, математик Гипатияның (370-415) трагедиялық тағдыры нақты мысал бола алады. Ол математик ретінде Аполлонийдің «конустың қималарына», Диофанттың «арифматикасына» түсініктемелер жазған. Сол кезде философиялық еңбектерімен танымал, ділмарлығымен жұртты аузына қаратқан ғылымға рим империясының түкпір-түкпірінен шәкірттер ағылып жатады екен. Грек әйелінің мұндай беделге ие болуы христиан дінін нық тұтқан адамдарға ұнамайды. Архиепиоскоп Кирилл мадақтарды өршіктіріп, айдап салып, Гипатияны шіркеуге апарып кескілеп өлтірткізеді.

Александрия ғылыми мектебі осылай құриды, грек мәдениеті мен ғылымның орталығы уақытша Афиныға ауысады. Александриядан мұнда белгілі комментатор Прокл (410-485) ауысып келіп, өзінің неоплатоника философиялық мектебін ұйымдастырады. Ол көптеген философиялық шығармаларымен қатар математика ғылымы үшін аса маңызды еңбегін – Евклидтің «Бастамаларының» бірінші кітабына түсініктеме жазады.Мұнда әсіресе гректердің геометриясының тарихы жүйелі түрде баяндалады.Ол бізге жетпеген Евдемнің «Геометрия тарихы»,Геминнің «Математика теорисы» тәріздес еңбектеріне сүйене отырып,математиканы топ-топқа бөліп,математика пәні және оның философияға қатысы жөнінде Евклид,Аполлоний,Герон,Порфирий,Папп,Птолемей,Посидоний шығармаларынан маңызды мағұлматтар мен деректер келтіреді.Проклдың түсініктемелері математиканы оқуды жаңа бастаған шәкірттерге арналған.

Прокл Евклидке математикалық жаңалық қоспаған.Тек бір жағдайда,Евклидтің бесінші постулатын Птолемейдің дәлелдеу әрекетін келтірген кезде,ол Птолемейге қарсы шығып өзінше дәлелдемекші болады.Мұнда Прокл жазықтықта жатқан екі түзудің ара қашықтығы шектеулі болады,сондықтан бір нүктеден бұрыш жасап шығатын екі түзуді шексіз соза берсек,олардың ара қашықтығы кез келген шекті шамадан артық болады деген ұйғарымды жабық түрде пайдаланады.Бірақ бұл ұйғарым дәлелдемекші постулаттың өзіне пара-пар еді.

Проклдың математиканың қалай пайда болуы жөніндегі мағұлматын келтірейік: «... көпшілік пікір бойынша,аудандарды өлшеу мақсатында геометрия Мысырда ашылған.Себебі Ніл өзенінің тасып әркімнің нақты жер шекарасын шайып кетіп отырғандықтан,бұған мысырлықтар мұқтаж болған. Барлық бастамалар кемелсіздіктен кемелділікке қарай дамитынын еске алсақ, онда басқа ғылымдар сияқты математиканың да бастау көзі практикалық қажеттілік екендігіне ешқандай таңғалуға болмайды. Міне, осылай, сезімнен ақылға, ақылдан пайымдауға көшу қарапайым да табиғи болады. Сөйтіп, сауда саттық және есеп шарттарынан финикиялықтарды дәл арифметика қалай басталса, жоғарыда көрсетілген себептерден Мысырда геометрияда солай ашылған».

Бір сөзбен айтқанда Проклдың Евклидке түсініктемелерін математиканың тарихи методологиясы, методикасы туралы жазылған бізге келіп жеткен тұңғыш ғылыми еңбек деп қараймыз.

Афины грек ғалымдарына тұрақты қоныс бола алмады. Діни қудалаудың зардабынан оқымыстылар тұрақтанбай, жан-жаққа кетті. Грек ғылымының ең соңғы өкілдері Константинопольда (қазіргі Стамбулда) қызмет істеген Проклдың шәкірттері милеттік Исидор мен тральдік Антемий Дамаскілік деп те атайды) болды. Олар Стамбулда атақты қасиетті София храмын салуға басшылық етеді. Исидор Евклидтің «Бастамларына» 15-кітапты қосқан деген мәлімет бар.

Осыдан кейін адамзат мәдениеті тарихына мәңгі өшпес із тастаған мың жылдық грек ғылымы жанып біткен шырақтай біржола сөнді. Грек математиктерінің бір кездегі жетістіктері кейіннен орта ғасырлардағы (Шығыс және Еуропа) Қайта өрлеу заманындағы оқымыстылардың матемтикалық зерттеулеріне, қазіргі математиканың қалыптасуына іргетас болып қаланады, оның әрі қарай дамуына шешуші ықпал жасады. Бұл байланыс, қарым-қатыстың кейбір қырларына кітабымыздың келесі тарауларының тиісті жерлерінде тоқталып отырамыз.