Нахождение точки пересечения прямой общего положения с плоскостью общего положения

Построим точку К - точку пересечения прямой общего положения а с плоскостью общего положения b, заданную тремя точками А, В, С.

Алгоритм построения точки пересечения:

Например на П1 проведем через заданную прямую а1 вспомогательную горизонтально проецирующую плоскость s1: а s и s П1.

Построим m1 - линию пересечения вспомогательной плоскости s1 с заданной плоскостью b1. Отметим точки 11 и 21 - точки пересечения прямой m1 и отрезков А1В1 и В1С1 соответственно.

Построим фронтальную проекцию прямой m, учитывая принадлежность точек 1 и 2 сторонам треугольника АВС.

Находим точку К2 - точку пересечения прямых m2 и а2: К2=m2 а2.

По линии связи находим первую проекцию точки К - точку К1.

Определяем видимость прямой а с помощью метода конкурирующих точек. На П2, правая часть прямой а2 (относительно точки К2) - видима, а левая часть прямой а2 - невидима. На П1, левая часть прямой а1 (относительно точки К1) - невидима, а правая часть прямой а1 - видима.

 

Прямые частного положения

1. Прямые уровня

Прямая, параллельная одной из плоскостей проекций, называется прямой уровня.

Горизонталь - прямая, параллельная горизонтальной плоскости

Фронталь - прямая, параллельная вертикальной плоскости

Профильная прямая - это прямая, параллельная профильной плоскости

2. Проецирующие прямые

Прямая, перпендикулярная какой-либо плоскости проекций, называется проецирующей прямой.

Горизонтально проецирующая прямая - прямая, перпендикулярная горизонтали

Фронтально проецирующая прямая - прямая, перпендикулярная вертикали

Профильно проецирующая прямая - прямая, перпендикулярная профильной плоскости

 

 

Развертка конуса

 

11. Расстояние от точки до плоскости равно длине перпендикуляра, опущенного из точки на эту плоскость. Пусть требуется найти расстояние от точки K до плоскости s (АВС).

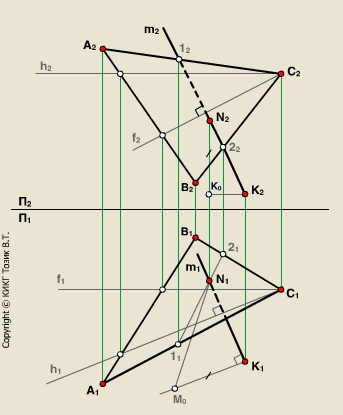
Нажмите на картинку для просмотра... Алгоритм построения:

Строится перпендикуляр из точки K на плоскость s (АВС): m1 h1, m2 f2.

Находится точка N - точка пересечения перпендикуляра m с плоскостью s (АВС).

Определяется расстояние от точки K до точки N с помощью прямоугольного треугольника K1N1M0. Длина гипотенузы N1M0 – это искомое расстояние: |KN| = N1M0.

Расстояние между параллельными плоскостями определяется длиной перпендикуляра, опущенного из произвольной точки одной плоскости до другой. Аналогично находится расстояние от плоскости до параллельной ей прямой. На прямой берется точка и находится расстояние до плоскости.

Все задачи на определение расстояний, углов, площадей, построение точек, прямых, плоских фигур по заданным параметрам могут быть решены на основе трех основных задач: построение перпендикуляра к плоскости, определение длины отрезка общего положения и построение точки пересечения прямой с плоскостью.

 

 

12. При решении задач инженерной графики в ряде случаев появляется необходимость в определении натуральной величины отрезка прямой линии. Решить эту задачу можно несколькими способами: способом прямоугольного треугольника, способом вращения, плоскопараллельного перемещения, заменой плоскостей проекций.

Рассмотрим пример построения изображения отрезка в истинную величину на комплексном чертеже способом прямоугольного треугольника. Если отрезок расположен параллельно какой-либо из плоскостей проекций, то на эту плоскость он проецируется в натуральную величину. Если же отрезок представлен прямой общего положения, то на одной из плоскостей проекций нельзя определить его истинную величину (см. рис. 69).

Возьмем отрезок общего положения АВ (A ^ П1) и построим его ортогональную проекцию на горизонтальной плоскости проекций (рис. 78, а). В пространстве при этом образуется прямоугольник А1ВВ1, в котором гипотенузой является сам отрезок, одним катетом — горизонтальная проекция этого отрезка, а вторым катетом — разность высот точек А и В отрезка. Так как по чертежу прямой определить разность высот точек ее отрезка не составляет труда, то можно построить по горизонтальной проекции отрезка (рис. 78, б) прямоугольный треугольник, взяв вторым катетом превышение одной точки над второй. Гипотенуза этого треугольника и будет натуральной величиной отрезка АВ.

Аналогичное построение можно сделать на фронтальной проекции отрезка, только в качестве второго катета надо взять разность глубин его концов (рис. 78, в), замеренную на плоскости П1.

 

Для определения натуральной величины отрезка прямой можно воспользоваться поворотом ее относительно плоскостей проекций, чтобы она расположилась параллельно одной из них (см. § 36) или вводом новой плоскости проекций (заменой одной из плоскостей проекций) так, чтобы она была параллельна одной из проекций отрезка