Определение 1 (теоретико – множественное)

МОДЕЛИ ДЛЯ РАЗРАБОТКИ ПРОГРАММНЫХ ПРИЛОЖЕНИЙ НА ПРИМЕРЕ МЕНЮ-ДИАЛОГОВОЙ СИСТЕМЫ

В статье предлагается вариант описания модели меню - диалоговой системы на основе теории взаимодействующих процессов CSP. С помощью средств этой теории строятся спецификации функций управления меню – диалогом. Рассматриваются функции для завершения меню – диалога на любом шаге выполнения, функции, позволяющие вернуться к любому из предыдущих шагов меню – диалога, а также функции – переключатели.

Ключевые слова: модель, программные спецификации, взаимодействующие процессы, формализованные средства,
диалоговые системы, технология программирования

Введение.

Сложность и многообразие современных программных приложений приводят к необходимости качественного изменения используемых технологических средств их разработки и реализации. Большинство из используемых технологических средств, основанных как правило на интуитивных подходах, не обеспечивают однозначность описания постановки задачи на программирование, предварительное исследование свойств программных приложений до этапа их непосредственной разработки и наконец высокую степень надежности программ. Целесообразным решением перечисленных выше проблем является использование формализованного подхода, обеспечивающего строгое и однозначное описание требований к создаваемому программному продукту. Наилучший эффект применения формализованных средств достигается в случае их адекватного использования на всех необходимых этапах разработки, начиная от постановки задачи до этапа непосредственной реализации и внедрения программного продукта. Такой подход обеспечивает возможность компактного описания и принятия обоснованных решений по методам реализации. Формализованный подход имеет много потенциальных преимуществ, от улучшения качества самой спецификации до автоматической генерации выполняемого кода. Основу формализованного подхода составляет построение формальной модели, с помощью которой обеспечивается не только описание соответствующих компонент программного продукта на всех этапах жизненного цикла программного обеспечения, но и проведение предварительных исследований по выбору оптимальных методов разработки и реализации. К настоящему времени известно множество различных формализованных средств построения моделей программных приложений, среди которых можно выделить теорию взаимодействующих процессов CSP [1], привлекательность которой обусловливается возможностями однозначного описания, исследования свойств и, наконец, эффективной реализации моделей программных приложений.

В предлагаемой статье рассматривается вариант построения модели программного приложения на основе теории CSP. В качестве примера программного приложения рассматривается меню - диалоговая система.

 

Модель меню - диалоговой системы.

Одним из существенных требований, предъявляемых к диалоговым систе­мам, является обеспечение удобного интерфейса с пользователем, который заключается в минимизации вводимых с терминала данных без потери мнемоники обозначений, уменьшении количества ошибок при вводе информации и, самое главное, в быстрой адаптации пользователя к диалоговой системе. Такой интерфейс является важным особенно в тех случаях, когда диалоговая система эксплуатируется «случайным» пользователем или вводимые в режиме диалога данные имеют сложную структуру. Существует много способов обес­печения указанного интерфейса, среди которых меню-диалог является одним из важных. Суть меню-диалога заключается в выдаче альтернативного списка элементов (меню), один из которых выбирается пользователем путем подвода курсора или нажатием соответствующей функциональной клавиши при диало­говом решении задачи на ЭВМ. Наиболее очевидные преимущества, достигае­мые при использовании меню - диалоговых систем, следующие:

1) быстрая адаптация пользователя к диалоговой системе и практически полное исключение необходимости специального изучения системы;

. 2) минимизация вводимой с терминала информации и, следовательно, уменьшение вероятности появления ошибок.

Меню - диалоговое взаимодействие адекватно описывается множеством по­следовательностей выбираемых из меню элементов. Последнее позволяет ис­пользовать для описания меню-диалога средства теории взаимодействующих процессов CSP. В CSP упо­мянутые выше последовательности называются следами, а каждый элемент последовательности определяет событие (например, функцию, вызываемую к дей­ствию после выбора соответствующего элемента). След -это конечная по­следовательность символов в заданном алфавите. Содержательно след опреде­ляет один из возможных путей прохождения меню - диалогового взаимодействия от начала его функционирования до определенного момента времени, а каж­дый символ следа обозначает одно из событий. Например, <а, b > обозначает след, состоящий из событий a и b. Множество всех символов, обозначающих события, которые могут быть вызваны функционированием заданного процес­са, называется алфавитом процесса. Процесс - это множество всех его следов, описывающих всевозможные пути его функционирования. Для любого процесса Р с алфавитом А имеют место следующие соотношения:

P0. PÍ A ^*, А*— множество всевозможных следов с символами из ал­фавита А (универсальное множество);

P1. <> Î P, где <> обозначает пустой след;

P2. st Î P => s Î P , для всех stÎ A ^*, st - конкатенация следа-s со следомt.

Ниже приводятся основные определения теории CSP, которые будут использоваться в дальнейшем.

Пусть s – непустой след (s≠<>), тогда s₀ означает начальный символ следа s, а s’ - результат удаления начального символа из s.

Пусть символ Ö означает событие успешного завершения процесса, тогда этот символ может появиться только в конце следа. Таким образом при рассмотрении последовательной композиции следов (s; t) след t может быть выполнен только при условии успешного завершения следа s.

Далее вводится отношение s £ t, которое определяется как

s £ t = _df $ u (su=t), в этом случае след s называется префиксом следа t. Например, <x,y> £ <x, y, z>, <> £ <x, y>.

Через (t éA) обозначается результат удаления всех символов из следа t, не принадлежащих множеству A. Например, <a, d, c, d> é {a,c} =<a, c>.

Выражение P⁰ обозначает множество всех событий, начиная с которых стартует процесс P. Формально это определяется как

P⁰ = _df { c | < c > Î P }.

Процесс FAIL = _df {<>} определяет пустой процесс, который ничего не делает, а процесс SKIP = _df {<>,<Ö >}, который также ничего не делает, в отличие от предыдущего процесса завершается всегда успешно.

Пусть c - некоторое событие, а P является процессом. Тогда (c → P) (“c затем P”) определяет процесс, который начинается с выполнения события c, после чего его дальнейшее поведение определяется процессом P. Формально это определяется как (c → P) = _df {(c→ s) | c Î aP & s Î P }, где (c→ s) = _df < c > s, а aP определяет алфавит процесса P.

Пусть P – некоторый процесс и s Î P, тогда операция P / s (P после s)

определяет новый процесс, который выполняется после того, как в процессе P была выполнена последовательность событий, определяемая следом s. Формальное определение: P / s = _df {t | st Î P}.

Пусть P и Q являются процессами, тогда операция P | Q определяется

как P | Q = _df P È Q, где a (P | Q) = aP È a Q. Данная операция является альтернативной операцией, предусматривающей выбор между P и Q. Выбор зависит от того, какое событие из множества (P | Q)⁰ будет выполнено. Например, если R=(a → P) | (b → Q), R/<a> =P и R/< b > = Q.

Пусть P и Q являются процессами, тогда последовательная композиция P; Q определяется поведением процесса P до его успешного завершения, после чего следует выполнение процесса Q. Формальное определение: P;Q = _df { s;t | s Î P & t Î Q }.

В CSP меню - диалоговое взаимодействие можно рассматривать как взаимодействующий с пользователем процесс P. Начальное меню, представляющее из себя множество стартовых событий процесса P, которое можно определить как P⁰. После того, как пользователь выбрал одно из событий, например x (xÎ P⁰), дальнейшее выполнение определяется процессом P/< x > (P после x), (P/< x.>) ⁰ ….

Выбор элементов меню активирует события по вызову соответствующих функций, среди которых есть проблемно – ориентированные, связанные с конкретными классами задач и функции, которые являются общими для различных классов задач. В первую очередь – это функции управления меню – диалогом.

Типичными функциями управления являются следующие:

(1) функции для завершения меню – диалога на любом шаге выполнения;

(2) функции, позволяющие вернуться к любому из предыдущих шагов меню - диалога;

(3) функции – переключатели – для переключения на запуск другого процесса, в частности, другого сценария меню – диалога, процесса ввода данных и т.п.

Цель представляемой статьи заключается в построении абстрактной модели меню – диалогового взаимодействия средствами теории CSP с формализованным описанием спецификаций функций управления меню – диалогом. Рассматриваются следующие функции управления меню – диалогового взаимодействия:

(1) “stop” – для завершения меню – диалога на любом шаге выполнения;

(2) “reset” – для восстановления начального состояния меню – диалога;

(3) “back” - для восстановления предыдущего состояния меню – диалога;

(4) функции – переключатели “off” и “on” для прерывания процесса с переключением на запуск другого процесса и восстановления работы прерванного процесса соответственно.

 

Функция “stop”.

Действие этой функции определяется процессом stoppable(P).

Пусть “stop” ÏaP (символ “stop” не принадлежит алфавиту процесса P). Тогда процесс stoppable(P) может быть определен как процесс, поведение которого определяется процессом P за исключением следующих условий:

(1) “stop” Î stoppable(P);

(2) символ “stop” появляется в каждом из меню процесса stoppable(P);

(3) при активации события “stop” процесс stoppable(P) успешно

завершает свою работу

Например:

<a, b, c, stop, Ö > Î stoppable(P) ó <a, b, c> Î P, где символ Ö означает событие успешного завершения процесса.

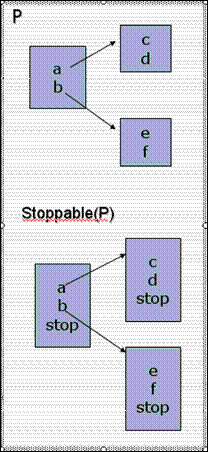
Рис.1. Пример представления процесса stoppable(P).

Для формального определения данного процесса будем использовать теоретико –множественный и процедурный способы определения процесса. Теоретико-множественное определение процесса предусматривает его представление в виде множества следов, определяющих поведение процесса, а процедурный задает процесс в виде пары < I, F >, где I определяет начальное состояние процесса, а F – функцию переходов. Теоретико-множественное определение является удобным для анализа и исследования свойств процесса, а процедурное

ориентировано на реализацию процесса.

Определение 1 (теоретико – множественное).

stoppable(P) = _df {st | sÎP & t Î(stop->SKIP)), где P является успешно

завершаемым процессом и stopÏaP.