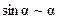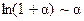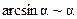К а ф е д р а «Высшая математика и
прикладная информатика»
ЛИНЕЙНАЯ АЛГЕБРА,
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ,
НАЧАЛА МАТЕМАТИЧЕСКОГО АНАЛИЗА
(для заочного факультета)
Учебно-методическое пособие
по специальным разделам высшей математики
Самара 2008
УДК 517.531, 519.2
Линейная алгебра, аналитическая геометрия, начала математического анализа (для заочного факультета): Учеб.-метод. пособ. по специальным разделам высшей математики/ Л.В. Лиманова, Л.А. Муратова; Самар. гос. техн. ун-т. Самара, 2008. 33 с.
Представлены задачи и их решения из следующих разделов курса высшей математики: «Линейная алгебра», «Аналитическая геометрия», «Математический анализ».
Для студентов заочного факультета СамГТУ.
Ил.2. Библиогр.: 6 назв.
Печатается по решению редакционно-издательского совета СамГТУ
В соответствии с программой курса высшей математики в 1 семестре на заочном факультете СамГТУ данная работа включает такие разделы, как линейная алгебра, аналитическая геометрия, теория пределов, дифференциальное исчисление.
Работа состоит из набора типовых задач из указанных разделов с подробными решениями и необходимым теоретическим материалом. Кроме того, в приложении 1 представлен тренировочный тест с ответами для самоконтроля знаний.
Материал данной работы рекомендуется использовать для подготовки к контрольной работе и экзамену по высшей математике на заочном факультете.
ЗАДАЧИ И РЕШЕНИЯ
Задача 1. Вычислить определитель  .
.
Решение. Определитель второго порядка  равен разности между произведениями элементов главной диагонали (a1 и b2) и побочной (b1 и a2), то есть
равен разности между произведениями элементов главной диагонали (a1 и b2) и побочной (b1 и a2), то есть
 .
.
Поэтому 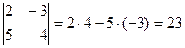 .
.
Задача 2. Вычислить определитель  .
.
Решение. Определитель третьего порядка можно вычислить по формуле
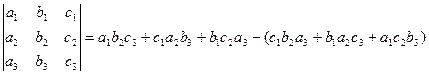
При этом полезна следующая схема. Первые три слагаемых – это произведения элементов, попавших на главную диагональ и в вершины двух треугольников (рис.1). Три слагаемых в скобках – это произведения элементов, попавших на побочную диагональ и в вершины двух других треугольников (рис.2).
 | |||
 | |||
Рис. 1 Рис. 2
Получаем

 .
.
Задача 3. Умножить матрицу  на матрицу
на матрицу  и найти сумму элементов третьей строки результирующей матрицы.
и найти сумму элементов третьей строки результирующей матрицы.
Решение. Известно, что матрицу A размера  (m − число строк, n − число столбцов) можно умножить на матрицу B размера
(m − число строк, n − число столбцов) можно умножить на матрицу B размера  , если n = p, причем в результате получится матрица
, если n = p, причем в результате получится матрица 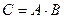 размера
размера  . Элемент cij (расположен на пересечении i- й строки и j -го столбца) результирующей матрицы C вычисляется по формуле
. Элемент cij (расположен на пересечении i- й строки и j -го столбца) результирующей матрицы C вычисляется по формуле
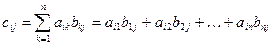 ,
,
то есть равен сумме произведений элементов строки i матрицы A на соответствующие элементы столбца j матрицы B.
В данной задаче матрицы A и B имеют размер  и
и  соответственно, и, значит, перемножаемы (n=p= 2), а результирующая матрица C будет иметь размер
соответственно, и, значит, перемножаемы (n=p= 2), а результирующая матрица C будет иметь размер  .
.
Найдем c11, для чего умножим поэлементно первую строку матрицы A на первый столбец матрицы B и результаты сложим:
 .
.
Вычислим c12, умножив первую строку матрицы A на второй столбец матрицы B и сложив результаты:
 .
.
Аналогично, находим остальные элементы
 ,
,  ,
,  ,
, 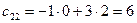 ,
,
 ,
,  ,
,
 ,
,  ,
,
 ,
,  .
.
Итак,
 .
.
При этом сумма элементов третьей строки матрицы C равна
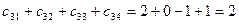 .
.
Задача 4. Решить систему уравнений, приняв в качестве базисных переменных y и z:

Решение. Решаем систему методом Гаусса. Запишем расширенную матрицу системы – матрицу из коэффициентов при неизвестных и свободных членов.


 ~
~
Среди коэффициентов при неизвестных в первом уравнении есть удобная для дальнейших вычислений 1, ей соответствует переменная z. Назовем z базисной переменной. Исключим базисную переменную z из 2-го уравнения, для чего умножим 1-е уравнение на 2 и сложим со вторым. Получим эквивалентную исходной систему уравнений с матрицей

 ~
~
Учитывая тот факт, что в каждом уравнении выбирается одна базисная единица и по условию задачи другой базисной переменной должен быть y, получим базисную единицу во 2-м уравнении, разделив его на (-2):



 ~
~
Исключим y из первого уравнения. Для этого умножим второе уравнение на 3 и сложим с первым:



Запишем систему уравнений, соответствующую последней матрице

Выразив базисные переменные у и z через свободную переменную х, получим общее решение системы уравнений

Задача 5. Найти длину вектора  .
.
Решение. Длину вектора 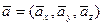 , или его модуль можно вычислить по формуле
, или его модуль можно вычислить по формуле
 .
.
Имеем  .
.
Задача 6. Векторы  и
и  образуют угол
образуют угол  . Зная, что
. Зная, что  ,
,  , найти скалярное произведение векторов
, найти скалярное произведение векторов  .
.
Решение. Согласно определению скалярное произведение векторов  и
и  равно
равно
.
Поэтому получим
.
Задача 7. Векторы и образуют угол. Известно, что,, а скалярное произведение векторов. Найти.
Решение. Выразим  из формулы скалярного произведения (см. задачу 6)
из формулы скалярного произведения (см. задачу 6)
 .
.
Задача 8. Вычислить скалярное произведение векторов  и
и  .
.
Решение. Используем формулу скалярного произведения векторов 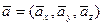 и
и  , согласно которой
, согласно которой
 .
.
Так как  ,
,  , то
, то
 .
.
Задача 9. Вычислить скалярное произведение  , если известно, что
, если известно, что  ,
,  ,
,  .
.
Решение. Найдем векторы  и
и  :
:
 ,
,
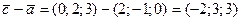 .
.
Согласно формуле скалярного произведения (см. задачу 8) получим
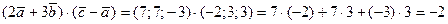 .
.
Задача 10. Найти  , при котором ортогональны векторы
, при котором ортогональны векторы  и
и  .
.
Решение. Условием ортогональности векторов 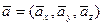 и
и  является равенство нулю их скалярного произведения
является равенство нулю их скалярного произведения
 .
.
Имеем  ,
,
или  , откуда
, откуда  .
.
Задача 11. Найти векторное произведение векторов  .
.
Решение. Вычисляем векторное произведение векторов 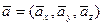 и
и  по формуле
по формуле
 .
.
Получаем
 .
.
Задача 12. Векторы  и
и  образуют угол
образуют угол  . Зная, что
. Зная, что 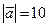 ,
,  , найти модуль векторного произведения векторов
, найти модуль векторного произведения векторов  .
.
Решение. В соответствии с определением векторного произведения имеет место формула
 .
.
Подставляя исходные данные, получим
 .
.
Задача 13. Известно, что  ,
,  и векторы
и векторы  и
и  образуют угол
образуют угол  . Найти
. Найти  .
.
Решение. Используя формулу модуля векторного произведения (см. задачу 12), найдем
 .
.
Поэтому
 .
.
Задача 14. Даны три вектора  ,
, 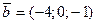 ,
,  . Найти:
. Найти:
1) смешанное произведение векторов  ;
;
2) объем параллелепипеда, построенного на векторах  ,
,  ,
,  ;
;
3) объем треугольной пирамиды, построенной на векторах  ,
,  ,
,  .
.
Решение. 1) Смешанное произведение векторов 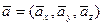 ,
,  ,
,  вычисляется по формуле
вычисляется по формуле
 .
.
Поэтому получаем
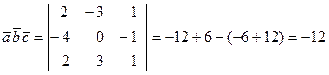 .
.
2) Объем параллелепипеда, построенного на векторах  ,
,  ,
,  , выражается через смешанное произведение и равен
, выражается через смешанное произведение и равен

3) Объем треугольной пирамиды, построенной на векторах  ,
,  ,
,  , составляет 1/6 объема параллелепипеда, построенного на тех же векторах, т.е.
, составляет 1/6 объема параллелепипеда, построенного на тех же векторах, т.е.

Задача 15. Определить  , при котором компланарны векторы
, при котором компланарны векторы  ,
,  ,
,  .
.
Решение. Векторы называются компланарными, если они параллельны одной плоскости. Условием компланарности трех векторов является равенство нулю их смешанного произведения:
 .
.
Приравнивая к нулю смешанное произведение векторов (см. задачу 14), получим уравнение для определения 
 .
.
Отсюда 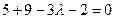 , значит
, значит  .
.
Задача 16. Составить уравнение плоскости, проходящей через три заданные точки А (1; 1; 1), В (1; 2; 3), С (2; 1; −1).
Решение. Воспользуемся уравнением плоскости, проходящей через три точки  :
:
 .
.
Получим
 ,
,
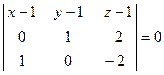 ,
,
 ,
,
 ,
,
 .
.
Задача 17. Составить уравнение плоскости, проходящей через точку
М (4; −1; 0) перпендикулярно вектору  .
.
Решение. Уравнение плоскости, проходящей через точку  перпендикулярно вектору
перпендикулярно вектору  имеет вид
имеет вид
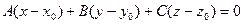 .
.
Подставив заданные значения, получим
 ,
,
или
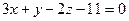 .
.
Задача 18. Составить уравнение плоскости, проходящей через точку М (2; 0; −3) параллельно плоскости  .
.
Решение. В уравнении плоскости вида

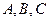 - координаты нормального вектора
- координаты нормального вектора  – вектора, перпендикулярного к плоскости.
– вектора, перпендикулярного к плоскости.
Таким образом, плоскость  имеет нормаль
имеет нормаль  .
.
Поскольку эта плоскость параллельна искомой, вектор  будет нормалью и к искомой плоскости. Осталось воспользоваться уравнением плоскости, проходящей через данную точку перпендикулярно данному вектору (см. задачу 17). Получим
будет нормалью и к искомой плоскости. Осталось воспользоваться уравнением плоскости, проходящей через данную точку перпендикулярно данному вектору (см. задачу 17). Получим
 ,
,
или
 .
.
Задача 19. Найти А и В, при которых плоскость  параллельна плоскости
параллельна плоскости  .
.
Решение. Нормальные векторы заданных плоскостей (см. задачу 18) соответственно равны  и
и  . Так как плоскости параллельны, их нормали коллинеарны, а условием коллинеарности векторов
. Так как плоскости параллельны, их нормали коллинеарны, а условием коллинеарности векторов  и
и  является пропорциональность их координат:
является пропорциональность их координат:

Поэтому получим
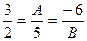 .
.
Отсюда следует, что А = 7,5, В = −4.
Задача 20. Составить канонические и параметрические уравнения прямой, проходящей через точку М (−2; 7; 0) параллельно вектору 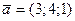 .
.
Решение. Канонические уравнения прямой, проходящей через точку  параллельно вектору
параллельно вектору  , имеют вид
, имеют вид
 .
.
Параметрические уравнения прямой можно получить, приравняв эти отношения к t

и выразив х, y и z через t:
 .
.
Заметим, что вектор  называют направляющим вектором прямой.
называют направляющим вектором прямой.
С учетом исходных данных задачи получаем канонические уравнения
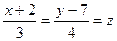
и параметрические уравнения искомой прямой
 .
.
Задача 21. Составить уравнения прямой, проходящей через точку М (4; 1; 5) параллельно прямой 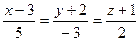 .
.
Решение. Прямая 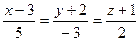 параллельна своему направляющему вектору
параллельна своему направляющему вектору  . Но тогда вектор
. Но тогда вектор  параллелен и искомой прямой. Воспользовавшись уравнением прямой, проходящей через данную точку параллельно данному вектору (см. задачу 20), получим
параллелен и искомой прямой. Воспользовавшись уравнением прямой, проходящей через данную точку параллельно данному вектору (см. задачу 20), получим
 .
.
Задача 22. Найти А и В, при которых параллельны прямые
 и
и  .
.
Решение. Если прямые параллельны, то их направляющие векторы  и
и  коллинеарны, значит, координаты направляющих векторов пропорциональны (см. задачу 19):
коллинеарны, значит, координаты направляющих векторов пропорциональны (см. задачу 19):
 .
.
Отсюда следует, что А = −0,5, В = −20.
Задача 23. Определить  , при котором перпендикулярны две прямые
, при котором перпендикулярны две прямые  и
и  .
.
Решение. Так как прямые перпендикулярны, их направляющие векторы  и
и 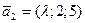 также перпендикулярны, но тогда скалярное произведение этих векторов равно нулю (см. задачу 10)
также перпендикулярны, но тогда скалярное произведение этих векторов равно нулю (см. задачу 10)
 ,
,
откуда  .
.
Задача 24. Составить уравнение прямой, проходящей через две точки М 1(2; −5; 1) и М 2(3; 4; −2).
Решение. Воспользуемся уравнением прямой, проходящей через две заданные точки  и
и 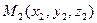 :
:
 .
.
Получим
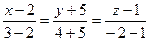 ,
,
или
 .
.
Задача 25. Составить уравнение плоскости, проходящей через точку М (1; −3; 0) перпендикулярно прямой  .
.
Решение. Так как прямая перпендикулярна плоскости, направляющий вектор  этой прямой также перпендикулярен плоскости.
этой прямой также перпендикулярен плоскости.
Согласно уравнению плоскости, проходящей через точку М перпендикулярно вектору  (см. задачу 17), получим
(см. задачу 17), получим
 , или
, или
 .
.
Задача 26. Составить уравнение прямой, проходящей через точку М (2; 7; −1) перпендикулярно плоскости  .
.
Решение. Так как прямая перпендикулярна плоскости, нормальный вектор  этой плоскости параллелен прямой. В соответствии с уравнением прямой, проходящей через точку М параллельно данному вектору
этой плоскости параллелен прямой. В соответствии с уравнением прямой, проходящей через точку М параллельно данному вектору  (см. задачу 20), имеем
(см. задачу 20), имеем
 .
.
Задача 27. Вычислить  .
.
Решение. При  числитель и знаменатель дроби неограниченно возрастают. В этом случае говорят, что имеет место неопределенность
числитель и знаменатель дроби неограниченно возрастают. В этом случае говорят, что имеет место неопределенность  . Выносим за скобки в числителе и знаменателе переменную в старшей степени и после сокращения получаем:
. Выносим за скобки в числителе и знаменателе переменную в старшей степени и после сокращения получаем:

 .
.
При  величины
величины  ,
,  ,
,  стремятся к 0,
стремятся к 0,  , весь числитель стремится к
, весь числитель стремится к  , а знаменатель
, а знаменатель  . Поэтому вся дробь стремится к
. Поэтому вся дробь стремится к  .
.
Таким образом, 
Задача 28. Вычислить  .
.
Решение. При  числитель и знаменатель стремятся к
числитель и знаменатель стремятся к  . Это неопределенность вида
. Это неопределенность вида  . Раскрываем ее (см. задачу 27):
. Раскрываем ее (см. задачу 27):
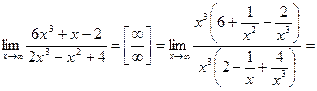
 .
.
Задача 29. Вычислить  .
.
Решение. Так как числитель и знаменатель при  стремятся к
стремятся к  , имеем неопределенность
, имеем неопределенность  . Раскрываем ее (см. задачу 27):
. Раскрываем ее (см. задачу 27):
 .
.
Поскольку при  числитель стремится к 3, а знаменатель − к
числитель стремится к 3, а знаменатель − к  , вся дробь стремится к 0 и
, вся дробь стремится к 0 и
 .
.
Задача 30. Вычислить  .
.
Решение. При  числитель и знаменатель дроби стремятся к 0. Это неопределенность вида
числитель и знаменатель дроби стремятся к 0. Это неопределенность вида 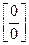 . Разложив числитель и знаменатель на множители и выполнив сокращение на множитель (х − 7), получим
. Разложив числитель и знаменатель на множители и выполнив сокращение на множитель (х − 7), получим
 .
.
Задача 31. Вычислить  .
.
Решение. Так как при  выражение
выражение  стремится к 1, а показатель степени
стремится к 1, а показатель степени  − к бесконечности, имеем неопределенность
− к бесконечности, имеем неопределенность  . Раскрываем ее с помощью второго замечательного предела
. Раскрываем ее с помощью второго замечательного предела
 .
.
Считая  , достраиваем выражение до второго замечательного предела и получаем
, достраиваем выражение до второго замечательного предела и получаем
 .
.
Задача 32. Вычислить  .
.
Решение. Поскольку при 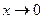 числитель и знаменатель дроби стремятся к 0, имеем неопределенность
числитель и знаменатель дроби стремятся к 0, имеем неопределенность 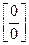 . Воспользовавшись формулами таблицы эквивалентности [приложение 2] для бесконечно малой величины
. Воспользовавшись формулами таблицы эквивалентности [приложение 2] для бесконечно малой величины  (
( ):
):

получим при  :
: 
Заменяя числитель и знаменатель на эквивалентные бесконечно малые величины, найдем
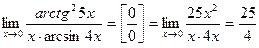 .
.
Задача 33. Вычислить  .
.
Решение. Имеем неопределенность 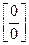 . Согласно формулам таблицы эквивалентности [приложение 2] для бесконечно малой величины
. Согласно формулам таблицы эквивалентности [приложение 2] для бесконечно малой величины  (
( )
)

поэтому при  :
:  .
.
Тогда
 .
.
Задача 34. Найти  , если
, если
 .
.
Решение. Применяя формулы дифференцирования произведения и частного
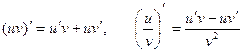 ,
,
имеем


и далее, с учетом формул дифференцирования элементарных функций [приложение 2]



получим

 .
.
Подставим в производную х = 2:
 .
.
Задача 35. Для функции  найти
найти  .
.
Решение. Применим правило дифференцирования сложной функции:
если y = y(u), u = u(x), то  .
.
В данном случае 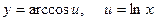 .
.
Поэтому [см. приложение 2]
 .
.
Тогда
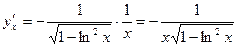 .
.
Задача 36. Для функции  найти
найти  .
.
Решение. По правилу дифференцирования сложной функции y = y(u), где u = u(x), имеем  .
.
Так как  , то [см. приложение 2]
, то [см. приложение 2]
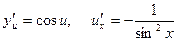 .
.
Окончательно,
 .
.
Задача 37. Найти интервалы возрастания и убывания функции  .
.
Решение. Функция y = f(x) возрастает, если  , и убывает, если
, и убывает, если  . Найдем
. Найдем  :
:
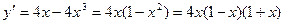 .
.
Определим знаки производной и промежутки монотонности функции
| x | 
| −1 | 
| 
| 
| ||

| + | − | + | − | |||
| y | 
| 
| 
| 
|
Итак, функция возрастает при  и убывает при
и убывает при  .
.
Задача 38. Найти интервалы выпуклости и вогнутости функции  .
.
Решение. Функция выпукла, если  и вогнута, если
и вогнута, если  . Найдем
. Найдем  :
:
 ,
,
 .
.
Определим знаки  и промежутки выпуклости и вогнутости функции
и промежутки выпуклости и вогнутости функции
| x | 
| −2 | 
| 
| 
| ||

| − | + | − | + | |||
| y | 
| 
| 
| 
|
Таким образом, функция выпукла при 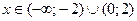 и вогнута при
и вогнута при  .
.
Приложение 1
Тренировочный тест
| № | Задания | Варианты ответов | ||||||||||||
| 1. | Вычислить  
| -17 | -1 | |||||||||||
| 2. |  Найти сумму элементов третьего столбца матрицы В.
Найти сумму элементов третьего столбца матрицы В.
| -39 | -9 | |||||||||||
| 3. | Решить систему уравнений, приняв в качестве базисных переменных x и z: 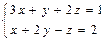 . .
| 
| 
| 
| 
| 
| ||||||||
| 4. | Векторы  и и  образуют угол образуют угол 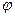 . Зная, что . Зная, что  , ,  , ,  , найти , найти 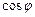 . .
| 
| 
| 
| 
| 
| ||||||||
| 5. | Вычислить  , если , если  , ,  , , 
| -19 | -2 | |||||||||||
| 6. | Определить  , при котором ортогональны векторы , при котором ортогональны векторы  и и  . .
| -5 | ||||||||||||
| 7. | Вычислить 
| 
| 
| 
| 
| 
| ||||||||
| 8. | Векторы  и и  образуют угол образуют угол  . Найти . Найти  , если , если  , , 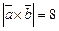 . .
| 
| 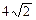
| 
| ||||||||||
| 9. | Если плоскость Сx+10y+4z+7=0 параллельна плоскости 3x-By+6z- 1 =0, то B+C= | -13 | -9 | |||||||||||
| 10. | Составить уравнение плоскости, проходящей через точку М (-1; 4; 5) перпендикулярно прямой 
| 
| 
| 
| 
| 
| |||||||
| 11. | Уравнение прямой, проходящей через точки А (2; -3; 5) и В (0; 4; -7), имеет вид | 
| 
| 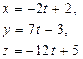
| 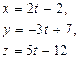
| 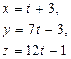
| |||||||
| 12. | Уравнение прямой, проходящей через точку М (2;4;-5) параллельно прямой 
| 
| 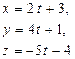
| 
| 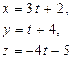
| 
| |||||||
| 13. | Прямые  и и 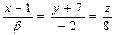 параллельны. Найти параллельны. Найти  . .
| -9 | -18 | ||||||||||
| 14. | Определить, при каком  перпендикулярны прямые перпендикулярны прямые  , , 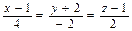 . .
| -1 | |||||||||||
| 15. | Вычислить 
| 
| 
| 
| 
| ||||||||
| 16. | Вычислить 
| 
| 
| 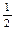
| |||||||||
| 17. | Вычислить 
| 
| 
| 
| 
| ||||||||
| 18. | Вычислить 
| 
| 
| ||||||||||
| 19. | Вычислить  , если , если 
| 
| 
| 
| 
| 
| |||||||
| 20. | Для функции  найти найти 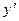
| 
| 
| 
| 
| 
| |||||||
| 21. | Для функции  найти найти 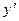 . .
| 
| 
| 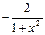
| 
| 
| |||||||
| 22. | Найти интервалы убывания функции 
| 
|  
| 
| 
| 
| |||||||
| 23. | Найти интервалы вогнутости функции 
| 
| 
| 
| 
| 
| |||||||
Правильные ответы
| № задания | ||||||||||||
| Ответ |
| № задания | |||||||||||
| Ответ |
Приложение 2
Таблица эквивалентности
Бесконечно малых
(справедлива при  )
)