Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.
Первый закон Кирхгофа: «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»
Второй закон Кирхгофа: «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».
Исследования трехфазной цепи при соединении фаз приемника по схеме “звезда”
Цель работы: исследование симметричных и несимметричных режимов работы трехфазной цепи при соединении фаз приемника по схеме “звезда” при наличии нейтрального провода (четырехпроводная цепь) и его отсутствии (трехпроводная цепь); изучение соотношений между фазными и линейными токами и напряжениями; построение векторных диаграмм токов и топографических диаграмм напряжений; исследование различных видов несимметрии приемника, в том числе аварийных режимов работы цепи; определение напряжения смещения нейтрали; приобретение навыков в разметке зажимов вторичных обмоток трехфазных трансформаторов; освоение методов расчета трехфазных цепей.
Рабочее задание
1. Ознакомиться с оборудованием лабораторного стенда в комплексе Electronics Workbench и приборами, применяемыми в работе.
2. Произвести разметку зажимов вторичной обмотки трехфазного трансформатора и соединить их по схеме “звезда”. Измерить фазные и линейные напряжения симметричного трехфазного источника и построить их топографическую диаграмму.
3. Собрать трехфазную цепь при соединении фаз резистивного трехфазного приемника (Ra, Rb, Rc) по схеме звезда с нейтральным проводом (рис. 4.1). Исследовать следующие режимы работы четырехпроводной трехфазной цепи:
а) симметричный режим (Ra=Rb=Rc);
б) несимметричный режим (Ra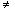 
Rb 
Rc);
в) обрыв одной из фаз (по указанию преподавателя).
Для каждого режима замерить фазные токи и ток в нейтральном проводе (Ia,Ib,Ic,IN), фазные напряжения приемника (Ua, Ub, Uc) и мощность каждой фазы источника ЭДС (PA,PB,PC). Результаты опытов занести в табл. 4. 1.
4. Отключить нейтральный провод и исследовать следующие режимы работы трехпроводной трехфазной цепи:
а) симметричный режим (Ra=Rb=Rc);
б) несимметричный режим (Ra 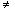Rb Rc);
в) обрыв одной из фаз (по указанию преподавателя).
Для каждого режима замерить фазные токи и ток в нейтральном проводе (Ia,Ib,Ic), фазные напряжения приемника (Ua, Ub, Uc), напряжение смещения нейтрали UnN и мощность каждой фазы источника ЭДС (PA,PB,PC). Результаты опытов занести в табл. 4.1.
5. Для каждого из проведенных в пп. 3 и 4 опытов рассчитать сопротивление каждой фазы приемника (Ra, Rb, Rc) и потребляемую ей мощность (Рa, Рb, Рc). Составить уравнение энергетического баланса трехфазной цепи и определить суммарные активные мощности источника и приемника. Данные занести в табл. 4.1.
6. Для четырехпроводной цепи по известным фазным напряжениям генератора (Ua, Ub, Uc) и сопротивлениям приемника (Ra, Rb, Rc) рассчитать для каждого режима ток в нейтральном проводе InN и сравнить полученные данные с экспериментальными данными. Результаты расчета занести в табл. 4.1.
7. Для трехпроводной цепи по известным фазным напряжениям генератора (Ua, Ub, Uc) и сопротивлениям приемника (Ra, Rb, Rc) рассчитать для каждого режима напряжение смешения нейтрали UnN и сравнить полученные данные с экспериментальными. Результаты расчета занести в табл. 4.1.
8. Для каждого из проведённых в пп. З и 4 опытов построить векторную диаграмму токов и топографическую диаграмму напряжений.
9. Дать краткий анализ полученных результатов по каждому проведенному опыту.
Творческое задание
1. Составить схему трехфазной цепи с включением приборов для измерения токов, напряжений и мощности при соединении симметричного источника и несимметричного приемника по схеме “звезда” с нейтральным проводом. В фазу А приемника включить батарею конденсаторов, в фазы B и С − одинаковую активную нагрузку (лампы накаливания). Собрать схему. Изменяя емкость батареи конденсаторов, добиться, чтобы все линейные токи цепи имели примерно одинаковые значения. Замерить и записать значения линейных токов, тока в нейтральном проводе, а также значение мощности каждой фазы источника ЭДС.
2. Отключить нейтральный провод. Замерить и записать значения линейных токов, мощность каждой фазы источника, а также фазные напряжения приемника и напряжение смещения нейтрали.
3. По результатам проведенных опытов определить комплексные сопротивления каждой фазы приемника, активные и реактивные мощности фаз источника и приемника, составить уравнения энергетического баланса активных и реактивных мощностей. Построить для каждого опыта векторные диаграммы токов и топографические диаграммы напряжений.
4. Изменить в трехпроводной цепи порядок чередования фаз источника, поменяв местами любые два зажима, к которым подключены линейные провода. Измерить фазные напряжения приемника. Построить топографическую диаграмму напряжений.
5. Сделать вывод об использовании данной схемы для определения последовательности фаз симметричного трехфазного источника.
Методические указания
К пункту 1
В качестве трехфазного источника ЭДС в лабораторной работе используются вторичные обмотки трехфазного трансформатора, которые после разметки соединяются в звезду. В качестве приемника пользуются три группы ламп накаливания, которые также соединяются по схеме “звезда”.
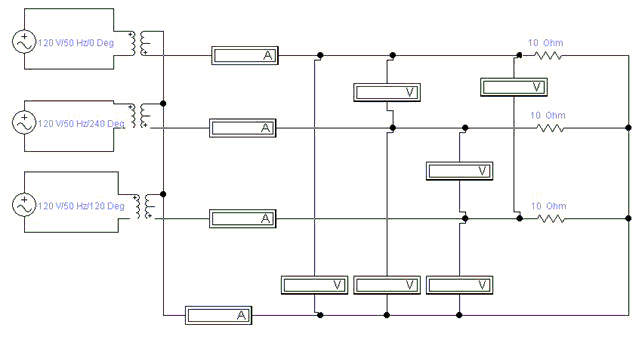
Схема для исследования трехфазной цепи с нейтральным проводом.
Схема для исследования трехфазной цепи без нейтрального провода.
Рис 4.1
К пункту 2
В симметричном трехфазном источнике амплитуды ЭДС всех его фаз равны по величине и сдвинуты по фазе относительно друг друга на угол 2П/3. В лабораторной работе в качестве трехфазного источника используются вторичные обмотки трехфазного трансформатора. При соединении обмоток по схеме “звезда” топографическая диаграмма фазных напряжений ( 
) будет иметь вид, приведенный на рис. 4. 2.
Рис. 4.2
Линейные напряжения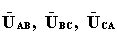 
по второму закону Кирхгофа будут равны разностям фазных напряжений:
(4.2)
В случае симметричного трехфазного генератора, обмотки которого соединены по схеме “звезда”, соотношение между действующими значениями фазных и линейных напряжений будет следующим:
Uл= 
UФ (4.3)
Разметка зажимов вторичных обмоток трансформатора начинается с измерения вольтметром напряжения каждой фазы в отдельности. Это позволяет определить зажимы, принадлежащее отдельным обмоткам.
Затем одна из обмоток выбирается в качестве основной (например, фазы А), и ее зажимы произвольно обозначаются как "начало" (А) и "конец" (X). Что дает возможность разметить зажимы других обмоток уже вполне определенно. Для этого "конец" первой обмотки соединяют с одним из зажимов второй обмотки и измеряют напряжение между свободными зажимами этих обмоток. Если измеренная величина больше фазного напряжения отдельной обмотки в раз, то свободный зажим обмотки соответствует ее "началу", если же измеренное напряжение равно фазному, то этот зажим является "концом" обмотки.
Приведенный выше метод позволяет разметить "начала" и "концы" обмоток трехфазного источника и соединить их по требуемой схеме.
Для определения последовательности фаз можно воспользоваться вращающимся фазоуказателем, имеющемся в комплекте К505, или выполнить творческое задание.
К пункту 5
При использовании в качестве приемника лампы накаливания схема замещения каждой фазы может быть представлена в виде активного сопротивления. Величины этих сопротивлений можно определить по закону Ома:
; 
; 
, (4.4)
где Ua, Ub, Uc − действующие значения фазных напряжений приемника; Ia, Ib, Ic − действующие токи фаз приемника, равные соответствующим линейным токам.
В случае активной нагрузки мощность каждой фазы приемника определяется простыми соотношениями:
Pa=UaIa; Pb=UbIb; Pc=UcIc. (4.5)
Мощность, отдаваемая трехфазным генератором в цепь, определится путем суммирования измеренных мощностей в каждой его фазе:
. (4.6)
Суммарная активная мощность приемника
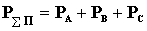
К пункту 6
Зная величину действующего значения фазного напряжения симметричного источника UФ, можно записать комплексы фазных напряжений всех его фаз:
; 
; 
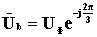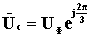. (4.7)
Если пренебречь внутренними сопротивлениями источников ЭДС и сопротивлениями соединительных проводов, то при наличии нейтрального провода фазные напряжения приемника будут равны фазным напряжениям источника как в симметричном, так и в несимметричном режиме. По известным комплексным сопротивлениям фаз приемника Za=Ra; Zb=Rb; Zc=Rc комплексные токи в каждой фазе определяются по закону Ома:
; 
; 
. (4.8)
Комплексный ток в нейтральном проводе 
no первому закону Кирхгофа будет равен сумме комплексных токов всех трех фаз:
. (4.9)
К пункту 7
Расчет трехпроводных трехфазных цепей в общем случае целесообразно производить, используя метод междуузлового напряжения. При этом напряжение смещения нейтрали 
будет равно:
, (4.10)
где 
; 
; 
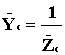− комплексные проводимости фаз приемника.
Зная напряжение UnN, можно определить напряжения и токи каждой фазы приемника:
; 
; 
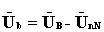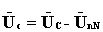. (4.11)
; 
; 
. (4.12)
При этом в любом режиме
. (4.13)
В случае симметричного приемника, как следует из уравнения (4.10) напряжение смещения нейтрали будет равно нулю и режим работы трехпроводной цепи ничем не будет отличаться от режима работы четырехпроводной цепи. Таким образом, наличие или отсутствие нейтрального провода не меняет симметричного режима работы трехфазной цепи.
К пункту 8
При построении топографических диаграмм напряжений трехфазной цепи необходимо различать диаграммы напряжений источника и диаграммы напряжений приемника. Топографическая диаграмма фазных и линейных напряжений симметричного трехфазного источника ЭДС, обмотки которого соединены по схеме “звезда”, приведена на рис.4.2. Если считать источники ЭДС идеальными, то вид этой диаграммы не будет зависеть от числа подключенных приемников и режимов их работы, а будет определяться только величиной ЭДС, создаваемой в каждой фазе генератора. Вид топографической диаграммы приемника будет зависеть от наличия или отсутствия нейтрального провода.
Если пренебречь сопротивлениями соединительных проводов, то начала фаз А,В,С источника ЭДС и начала фаз а,b,с приемника будут иметь одинаковые значения электрических потенциалов. При наличии нейтрального провода потенциалы нейтральных точек источника и приемника также равны и топографическая диаграмма напряжений приемника вне зависимости от режима его работы будет в точности совпадать с топографической диаграммой источника.
При отсутствии нейтрального провода потенциалы нейтральных точек источника и приемника согласно (4.10) будут равны только в случае симметричного приемника. Во всех других режимах появится напряжение смещения нейтрали UnN и согласно (4.11) фазные напряжения приемника будут несимметричными.
В качестве примера на рис. 4. 3 приведены векторные диаграммы токов и топографические диаграммы напряжений, построенные для различных режимов работы приемника, имеющего активную нагрузку.
Рис. 4.3,а соответствует симметричному режиму работы приемника. Токи во всех фазах равны по величине и совпадают по фазе с соответствующими фазными напряжениями приемника.
Рис. 4.3,б соответствует несимметричному режиму работы приемника при наличии нейтрального провода, когда Ra>Rb>Rc. Благодаря нейтральному проводу напряжения на фазах приемника остаются симметричными, однако токи в фазах будут теперь несимметричны. В нейтральном проводе будет протекать ток IN, который согласно (4.9) определится как геометрическая сумма векторов фазных токов.
На рис. 4.3,в представлена векторная диаграмма токов и топографическая диаграмма напряжений в случае обрыва линейного провода фазы С и наличия нейтрального провода. Вследствие обрыва ток фазы С и напряжение приемника фазы С будут равны нулю. Режимы работы фаз А и В не изменятся. В нейтральном проводе будет протекать ток IN=IA+IB.
Рис. 4.3,г соответствует несимметричному режиму работа приемника без нейтрального провода. Положение точки n на топографической диаграмме определится по формуле (4.10). Если известны действующие значения фазных напряжений приемника Ua,Ub,Uc, то положение точки n можно найти графически. Для этого нужно циркулем из точек А, В и C провести окружности, радиусы которых в масштабе равны соответствующим фазным напряжениям приемника. Точка пересечения этих окружностей даст положение точки n. Так как нагрузка приемника активная, фазные токи совпадают по фазе с соответствующими фазными напряжениями приемника. В соответствии с первым законом Кирхгофа геометрическая сумма векторов этих токов равна нулю.
На рис. 4.3,д построены векторная диаграмма токов и топографическая диаграмма напряжений при отсутствии нейтрального провода и обрыве линейного провода фазы А. В этом случае сопротивления в фазах В и получаются соединенными последовательно и включенными на линейное напряжение Ubc источника. При этом
;
;
;
.
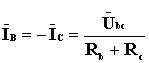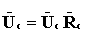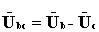Если Rb=Rc, то на каждое из этих сопротивлений приходится половина линейного напряжения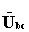 
. Точка n при этом на топографической диаграмме будет находиться на середине отрезка ВС.
Рис. 4.3, в соответствует короткому замыканию фазы А приемника при отсутствии нейтрального провода. В этом случае потенциалы точек А и n становятся одинаковыми (Ra=О). Фазные напряжения Ub и Uc на резисторах Rb и Rc равны линейным напряжениям Ub=Uba и Uc=Uca. Токи Ib и Ic совпадают по фазе с соответствующими фазными напряжениями приемника. Ток Ia определяется из первого закона Кирхгофа:
.
К пункту 9
При выполнении этого пункта необходимо отметить характерные особенности каждого из исследуемых режимов работы трехфазной цепи. Кроме того, укажите, какие, на ваш взгляд, измерения и вычисления при заполнении табл. 4.1 можно не делать, а воспользоваться результатами уже проведенных опытов или расчетов.
а) б)
в) г)
д) е)
Рис.4.3
