Векторная функция скалярного аргумента. Векторы скорости и ускорения. Кривизна плоской кривой

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 1 (0,138 ЗЕ)

 

Пределы: а) Раскрытие неопределенностей

б) Непрерывность. Точки разрыва

 

 

Срок выполнения 1-2 недели семестра

 

Выполнил студент группы ЭП-111

Белоусов А.А.

 

Работу принял

 

 

 

Кемерово 2011

 

Содержание работы

 

 

1. Раскрытие неопределенности

2. Порядок малости бесконечно малых. Эквивалентные бесконечно малые.

3. Раскрытие неопределенности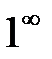

4. Определение характера точек разрыва функции

5. Контрольные вопросы

 

 

Литература [1,2,8,14,17]

 

 

Замечания преподавателя.

 

 

1. Раскрыть неопределенности

 

, ,

 

, ,

 

, .

 

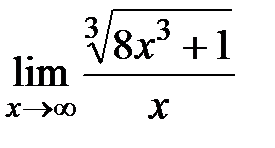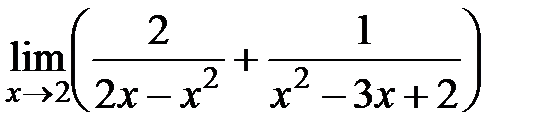2. Раскрыть неопределенности, используя эквивалентные бесконечно малые функции

 

, , ,

 

,

 

 

3. Раскрыть неопределенности

 

, , ,

, ,

 

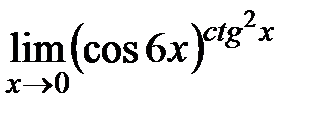
4. По формулам функций схематически построить их графики. В точках разрыва вычислить односторонние пределы и указать характер точек разрыва:

, , .

 

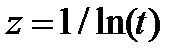
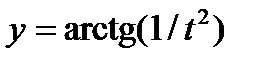Контрольные вопросы

 

1. Свойства функций: четность, периодичность, монотонность, нули функции.

2. Свойства и графики основных элементарных функций: степенная, показательная, логарифмическая, тригонометрические функции, обратные тригонометрические функции, гиперболические функции, обратные гиперболические функции

3. Дайте определение обратной функции. Для указанных функций найти выражение для обратной функции. Построить в одних координатных осях графики прямой и обратной функций: , , , , ,

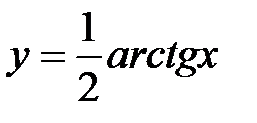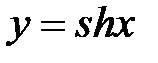4. Первый замечательный предел

5. Второй замечательный предел

6. Приведите примеры основных элементарных функций, которые являются четными

7. Приведите примеры основных элементарных функций, которые являются нечетными

8. Приведите примеры основных элементарных функций, которые являются бесконечно малыми в окрестности нуля.

9. Приведите примеры основных элементарных функций, которые являются ограниченными на бесконечности

10. Приведите примеры основных элементарных функций, которые являются бесконечно большими в окрестности нуля

11. Опишите основные свойства функции по формуле: , ,

, , ,

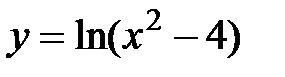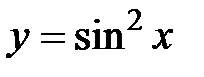12. Что такое неопределенности? Перечислите основные неопределенности.

13. Какие способы раскрытия неопределенности при условии Вы знаете? Приведите примеры.

14. Приведите пример раскрытия неопределенности при условии

15. Дайте определение функции, непрерывной в точке

 

16. Дайте определение точки разрыва первого рода. Приведите примеры

 

17. Приведите примеры точки устранимого разрыва

 

18. Дайте определение точки разрыва второго рода. Приведите примеры.

 

 

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

 

 

Направление подготовки 140400.62

«Электроэнергетика и электротехника»

 

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 2 (0,138 ЗЕ)

 

Техника дифференцирования

 

 

Срок выполнения 1-2 недели семестра

 

Выполнил студент группы ЭА- 111

Петров А.В.

 

Работу принял

 

 

 

Кемерово 2011

 

Содержание работы

 

 

1. Таблица производных. Производные арифметических операций

2. Производная сложной функции

3. Производная функции, заданной неявно

4. Производная функции, заданной параметрически

5. Дифференциал. Применение к приближенным вычислениям

6. Геометрический смысл производной. Уравнение касательной

7. Механический смысл производной

8. Контрольные вопросы

 

 

Литература [1,2,8,17]

 

 

Замечания преподавателя.

 

1. Вычислить производные, используя линейность операции дифференцирования и правила дифференцирования произведения и частного:

 

 

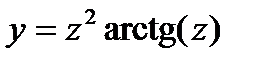
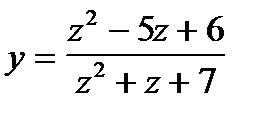
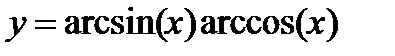
2. Вычислить производные, используя правило дифференцирования сложной функции (выписывать цепочку промежуточных переменных):

 

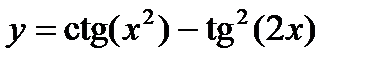
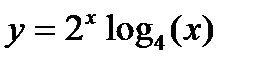
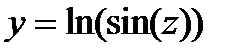
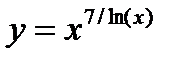
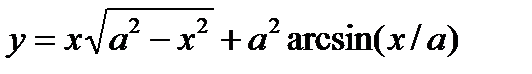
3. Найти производную функции, заданной неявно:

 

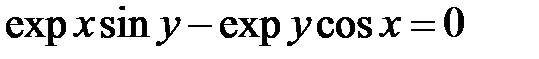а) ; б)

 

4. Найти производную функции, заданной параметрически:

 

а) ; б)

 

 

5. Применение дифференциала для приближенных вычислений

 

а) Найдите приближенное выражение для приращения объема при изменении давления на при условии постоянства температуры , если связаны законом

 

б) Вычислить приближенно значение функции при помощи дифференциала

 

6. Геометрический смысл производной

а) Под каким углом график функции 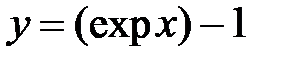пересекает ось абсцисс?

б) В каких точках и под каким углом пересекаются графики функци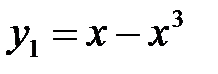й

и

в) Напишите уравнение касательной к кривой в указанной точке

 

6. Физический смысл производной:

а) Точка движется по параболе 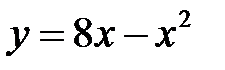так, что ее абсцисса изменяется по закону ( -измеряется в метрах, а 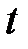- в секундах). Какова скорость изменения ординаты через 9 сек после начала движения?

б) В какой момент 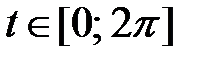надо устранить действие сил, чтобы точка,участвующая в гармоническом колебании , продолжала двигаться равномерно со скоростью

 

Контрольные вопросы

 

1. Дайте определение дифференцируемой функции и производной в точке

 

2. В чем состоит геометрический смысл производной?

 

3. В чем состоит физический смысл производной?

 

4. Как связаны производные прямой и обратной функции?

 

5. Сформулируйте правило дифференцирования сложной функции

 

 

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

 

 

Направление подготовки 140400.62

«Электроэнергетика и электротехника»

 

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 3 (0,417 ЗЕ)

 

Основные методы интегрирования

 

 

Срок выполнения 3-4 недели

 

Выполнил студент группы ЭА- 111

Петров А.В.

 

Работу принял

 

 

 

Кемерово 2011

 

Содержание работы

1. Таблица интегралов

2. Замена переменной

3. Интегрирование дробно-рациональных и иррациональных функций

4. Интегрирование по частям

5. Интегрирование тригонометрических и гиперболических функций. Тригонометрические и гиперболические подстановки

 

Литература: [1, 2, 9,17]

 

Замечания преподавателя

 

 

1. Найти интегралы, выполнив тождественные преобразования, используя линейность операции интегрирования

 

2. Найти интегралы, пользуясь подведением производной под знак дифференциала :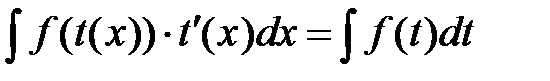

 

 

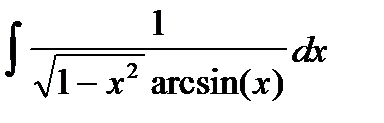
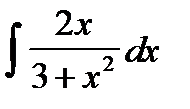
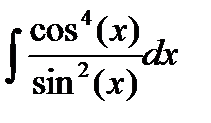
1. Найти интегралы, разбивая правильные дроби на сумму простейших дробей или выделяя целую часть и остаток для неправильных дробей

 

 

1. Найти интегралы при помощи замены с выделением полного квадрата (можно использовать формулы , ):
   
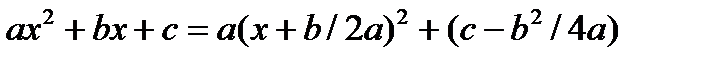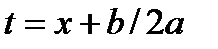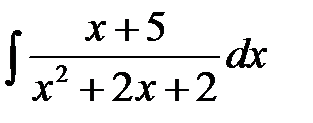
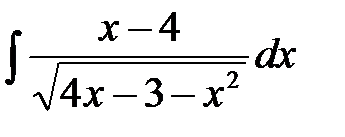
2. Найти интегралы, преобразуя подынтегральные функции с использованием степенных подстановок

 

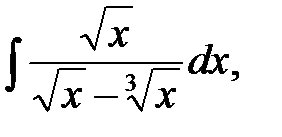
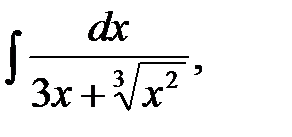
6. Найти интегралы, используя формулу интегрирования произведения

 

(интегрирование по частям)

 

 

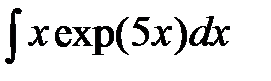
7. Найти интегралы, комбинируя рассмотренные выше элементарные приемы:

 

8. Проинтегрировать дробно-рациональные дроби:
,

 

9. Проинтегрировать тригонометрические функции:

 

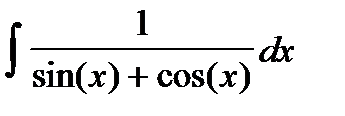
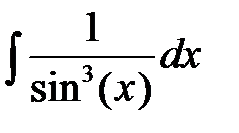
10. Проинтегрировать гиперболические функции:

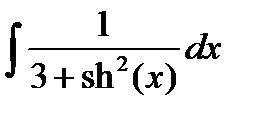
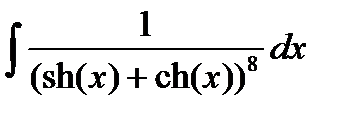
11. Найти интегралы, избавляясь от квадратных корней при помощи тригонометрических или гиперболических подстановок:

 

12. Найти интегралы, комбинируя различные приемы:

 

 

 

 

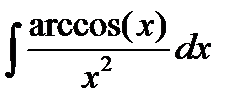
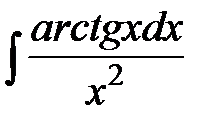
Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

 

 

Направление подготовки 140400.62

«Электроэнергетика и электротехника»

 

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 4 (0,278 ЗЕ)

 

Применение определенного интеграла к решению задач геометрии и физики

 

 

Срок выполнения 5-8 недели

 

Выполнил студент группы ЭА- 111

Петров А.В.

 

Работу принял

 

 

 

Кемерово 2011

 

Содержание работы

1. Вычисление площади плоской фигуры.

2. Вычисление объема тела вращения.

3. Вычисление длины дуги.

4. Вычисление работы, давления, момента инерции.

5. Оценки определенных интегралов. Приближенное вычисление определенных интегралов

 

Литература [1,2,9,17]

 

 

Замечания преподавателя

 

1. Вычислить определенные интегралы

 

а) 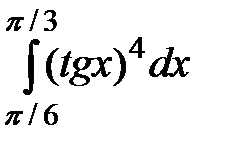, б) , в) , г)

 

 

2. Найдите площадь фигуры, ограниченной кривыми:

а) , ,

б)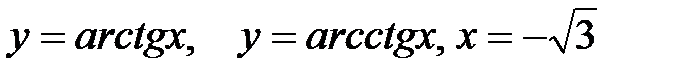

в)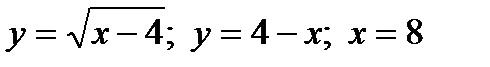

 

 

2.Найдите объем тела, образованного вращением фигуры, ограниченной линиями, вокруг заданной оси:

 

1) вокруг оси

2) вокруг оси

 

 

3.Найдите длину дуги кривой:

 

4.

а). Определите работу, затрачиваемую на выкачивание жидкости плотности из емкости в форме полушара радиуса

 

б). Определите давление жидкости плотности на боковые стенки цилиндрического сосуда цилиндрической формы радиуса

 

в). Найдите момент инерции прямоугольного треугольника с катетами и при вращении треугольника вокруг одного из катетов

5. Приближенное вычисление определенных интегралов

 

а)Оценить интеграл

б) Найти приближенно при (вычислять с четырьмя знаками после запятой) интеграл по формуле прямоугольников, по формуле трапеций, по формуле Симпсона

 

 

Контрольные вопросы

 

1. Дайте определение понятия «определенный интеграл». Условие существования определенного интеграла (интегрируемость функции)

2. Геометрический смысл определенного интеграла

3. Интеграл с переменным верхним пределом.

4. Формула Ньютона-Лейбница

5. Оценка определенного интеграла. Формула среднего значения

6. Несобственный интеграл с бесконечными пределами интегрирования

7. Несобственный интеграл от неограниченных функций

8. Признак сходимости несобственных интегралов

9. Формулы прямоугольников, трапеций, Симпсона

 

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

 

 

Направление подготовки 140400.62

«Электроэнергетика и электротехника»

 

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 5 (0,278 ЗЕ)

 

Степенные ряды и их применение

 

 

Срок выполнения 5-8 недели

 

Выполнил студент группы ЭА- 111

Петров А.В.

 

Работу принял

 

 

 

Кемерово 2011

 

Содержание работы

1. Таблица разложения в степенные ряды основных элементарных функций (с выводом)

2. Техника разложения функций в степенной ряд (ряд Маклорена, ряд Тейлора)

3. Применение степенных рядов к вычислению пределов (раскрытию неопределенностей)

4. Применение степенных к вычислению асимптот графиков функций

5. Применение степенных рядов к приближенному вычислению интегралов

 

Литература [1,2, 14,16]

 

 

1. Получить разложения в ряд Маклорена для основных элементарных функций: экспонента, логарифмическая функция, тригонометрические функции, обратные тригонометрические функции, гиперболические, обратные гиперболические функции

 

2. Используя таблицу разложений функций в ряд Маклорена, разложить функцию в ряд с заданной точностью . Для бесконечно малых указать степенной порядок малости:

 

; ;

 

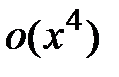
3. Разложить функцию по формуле Тейлора вблизи указанной точки с требуемой точностью :

 

 

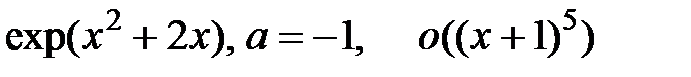
4. Написать приближенные формулы, описывающие поведение функции при больших значениях переменной (найти асимптоты графика функции наклонные или горизонтальные):

 

 

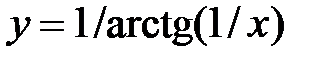
5.Написать приближенные формулы, описывающие поведение функции в окрестности ее нулей и точек разрыва:

 

 

 

 

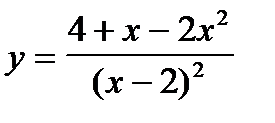
6. Раскрыть неопределенности:

 

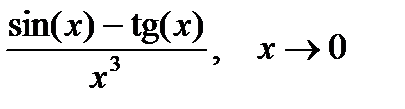
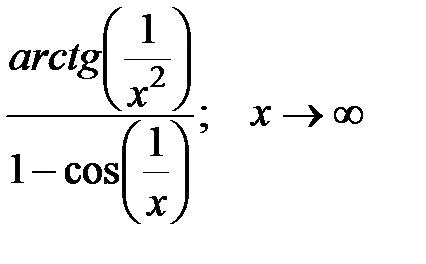
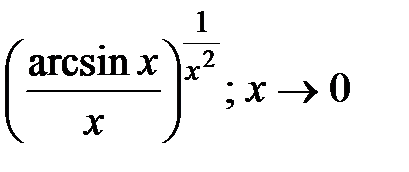
7.Написать формулы для приближенного вычисления интегралов при помощи разложения функций в степенной ряд. Указать область сходимости ряда.

 

3.

 

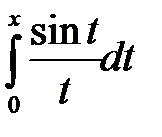
Контрольные вопросы

 

1.Числовой ряд. Определение суммы ряда

2. Ряд из членов геометрической прогрессии. Условия сходимости. Приведите примеры.

3. Необходимый признак сходимости числового ряда. Гармонический ряд

4. Критерий сходимости числового ряда с неотрицательными членами

5. Достаточные условия сходимости ряда. Признак сравнения

6. Достаточные условия сходимости ряда. Признак Даламбера

7. Достаточные условия сходимости ряда. Признак радикальный Коши

8. Достаточные условия сходимости ряда. Интегральный признак. Условия сходимости ряда

9. Теорема Тейлора. Формула Маклорена. Ряд Тейлора. Ряд Маклорена.

10. Получите разложение в ряд Маклорена для функции

11. Получите разложение в ряд Маклорена для функции

12. 4.Получите разложение в ряд Маклорена для функции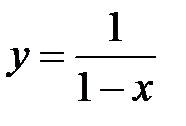

13. Чему равен коэффициент разложения функции в ряд Тейлора по степеням

14. Интервал сходимости ряда равен 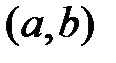. Сумма

15. Чему равна производная порядка в точке функции ?

16. Как определить степенной порядок малости при помощи разложения в ряд Тейлора в окрестности точки? Приведите примеры.

17. Как можно определить степенной порядок роста бесконечно большой в окрестности точки разрыва 2 рода?

18. Что называют наклонной (горизонтальной) асимптотой графика функции? Какие способы нахождения асимптот Вы знаете? Как использовать теорему Тейлора для нахождения асимптот? Приведите примеры.

 

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

 

 

Направление подготовки 140400.62

«Электроэнергетика и электротехника»

 

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 6 (0,278 ЗЕ)

 

Применение производной к исследованию функций

 

 

Срок выполнения 9-12 неделя

 

 

Выполнил студент группы ЭА- 111

Петров А.В.

 

Работу принял

 

 

 

Кемерово 2011

 

Содержание работы

1. Полное исследование функции и построение графика

2. Раскрытие неопределенностей с использованием правила Лопиталя

3. Задачи на наибольшее и наименьшее значения функции

 

Литература [1,2,8,17]

 

 

Замечание преподавателя

 

 

1. Провести полное исследование и построить графики функций (область определения, четность, нули функции, точки разрыва, вертикальные асимптоты, поведение при больших значениях аргумента – наклонные и горизонтальные асимптоты, локальные экстремумы, точки перегиба) (построить 2 функции по заданию преподавателя):

, , ,

 

 

2. Найдите наибольшее и наименьшее значения функции на отрезке:

 

а) ,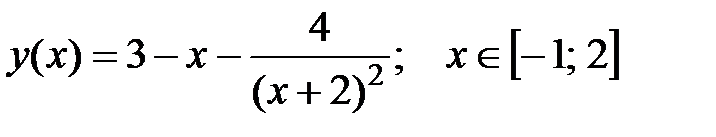

б)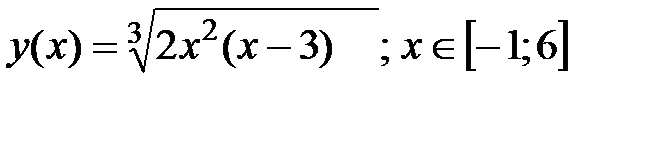

3. Написать приближенные формулы, описывающие поведение функций вблизи точек локальных экстремумов и точек перегиба
,

 

 

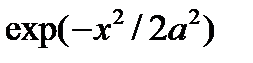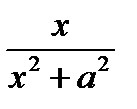
4. Раскрыть неопределенности, используя правило Лопиталя:

 

 

 

 

 

 

5. Решите задачи (две задачи по выбору)

а) Найти угловой коэффициент прямой, проходящей через точку и отсекающей от координатных осей треугольник наименьшей площади

(.

 

б) Объем правильной треугольной призмы 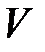. Какова должна быть сторона основания, чтобы полная поверхность была наименьшей?

в) В треугольник с основанием и высотой вписать прямоугольник с наименьшим периметром.

г) В шар радиуса вписать цилиндр наибольшего объема

д) Около заданного шара описать конус наименьшего объема

Контрольные вопросы

1. Сколько асимптот имеет график функции , , ?

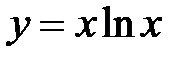2. Дайте определение точки локального экстремума функции

3. Сформулируйте необходимые условия существования экстремума

4. Сформулируйте достаточные условия существования экстремума

5. Дайте определение точки перегиба графика функции и сформулируйте необходимые условия его существования

 

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

 

 

Направление подготовки 140400.62

«Электроэнергетика и электротехника»

 

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 7 (0,139 ЗЕ)

 

Системы линейных уравнений

 

 

Срок выполнения 9-12 неделя

 

Выполнил студент группы ЭА- 111

Петров А.В.

 

Работу принял

 

 

 

Кемерово 2011

 

Содержание работы

1. Обратная матрица.

2. Решение матричных уравнений.

3. Ранг матрицы. Теорема Кронекера-Капелли.

4. Решение систем линейных уравнений методами обратной матрицы, Крамера, Гаусса

 

 

Литература [1,7,17]

 

Замечание преподавателя

 

1. Дайте определение обратной матрицы и сформулируйте условия ее существования. Для указанных матриц проверьте выполнение условий существования обратной матрицы и, если обратная матрица существует, то найдите ее:

, , , .

 

Ответы: , ,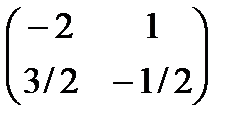

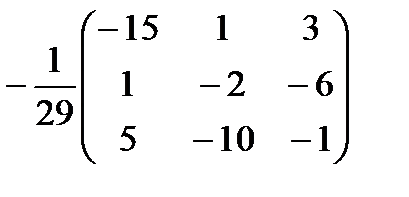
2. Выполняя действия над матрицами, найдите неизвестную матрицу из указанных уравнений: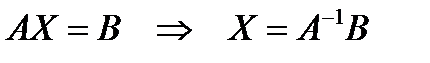

 

a) 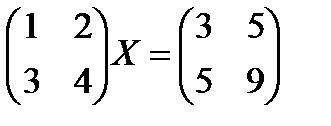, b) ,

с) Найдите матрицу 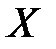из уравнения: , где , ,

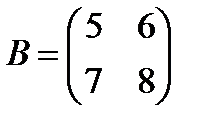d ) . Здесь , , .

 

Ответы: а) , b) , c) , d)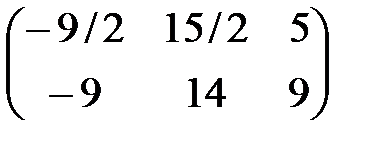

3. Дайте определение понятия ранг матрицы. Найдите ранг матрицы методом элементарных преобразований:

а) , б) , в) , г) ,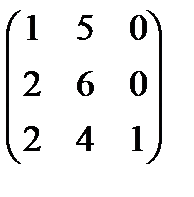

д)

 

4. Для каждой из указанных ниже систем

· методом элементарных преобразований определите ранг матрицы системы и ранг расширенной матрицы,

· на основании теоремы Кронекера-Капелли сделайте вывод о совместности системы (определите число решений системы),

· найдите решения системы, при этом, если решений множество, то укажите число базисных и свободных переменных

 

,

 

 

,

 

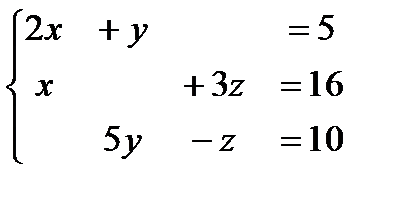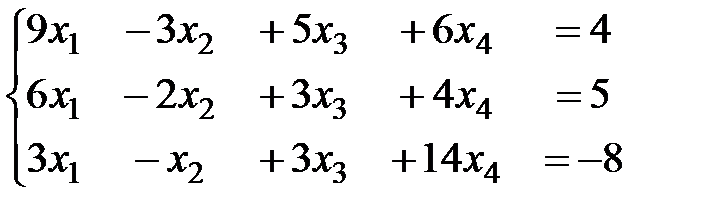
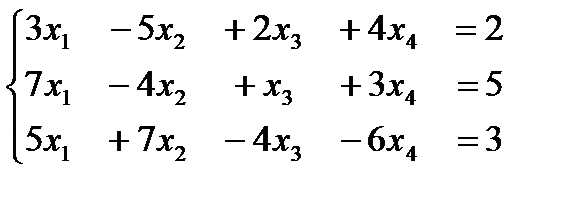Ответы: 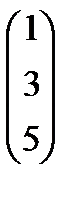, , не имеет решений, .

Контрольные вопросы

 

1. Что такое порядок матрицы?
2. Матрица, стоящая слева имеет 5 столбцов и 3 строки, а матрица, стоящая справа имеет 2 столбца и 8 строк. Можно ли перемножить такие матрицы?
3. Является ли матрица вырожденной?
4. Сколько решений имеет система линейных уравнений, если ранг матрицы системы равен рангу расширенной матрицы и равен 3, а число неизвестных равно 5?
5. Справедливо ли утверждение: все уравнения системы линейно независимы и система имеет единственное решение?

 

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

 

 

Направление подготовки 140400.62

«Электроэнергетика и электротехника»

 

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 8 (0,417 ЗЕ)

 

Аналитическая геометрия на плоскости

 

Срок выполнения - 12 неделя (прямая на плоскости -0,139 ЗЕ)

- 13 неделя (0,278 ЗЕ)

 

Выполнил студент группы ЭА- 111

Петров А.В.

 

Работу принял

 

 

 

Кемерово 2011

 

 

Содержание работы

1. Прямая линия на плоскости

2. Кривые второго порядка

3. Полярная система координат

4. Векторная функция скалярного аргумента

 

Литература [1,7,17]

 

 

Замечания преподавателя

 

Прямая линия на плоскости

1. Точка является вершиной квадрата, одна из сторон которого лежит на прямой линии . Вычислить площадь квадрата.

 

2. Найти точку пересечения медиан треугольника, вершинами которого являются точки .

 

3. Записать уравнение прямой, проходящей через начало координат и образующей угол 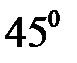с прямой линией .

 

4. Точка является вершиной квадрата, диагональ которого лежит на прямой . Написать уравнения сторон и второй диагонали этого квадрата.

 

Кривые второго порядка

 

а) Постройте кривые и укажите их основные характеристики

; ;

б) Установите, какие линии определяются уравнениями и схематично их постройте:

ü

ü

ü

ü

ü

 

Примечание. В последнем случае используйте поворот системы координат на угол согласно соотношениям

 

 

6. Найдите координаты фокуса параболы по координатам ее вершины и уравнению ее директрисы .

Ответ:

 

7. На гиперболе найти точку, ближайшую к точке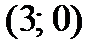

 

Векторная функция скалярного аргумента. Векторы скорости и ускорения. Кривизна плоской кривой.

 

а). По уравнению движения определите траекторию движения (годограф), вектор скорости, вектор ускорения, тангенциальную и нормальную составляющие вектора ускорения для моментов и .

 

б) По уравнению движения определите траекторию движения (годограф), вектор скорости, вектор ускорения, тангенциальную и нормальную составляющие вектора ускорения для моментов и .

 

в). Найдите кривизну в вершинах эллипса в вершинах эллипса.

 

9.Полярная система координат:

 

а) Постройте кривые в полярной системе координат:

, , ,

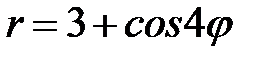
б) Найти площадь фигуры, ограниченной какой-либо кривой, указанной в предыдущем задании

 

в) Найдите длину дуги кривой

 

Контрольные вопросы

 

1. Линейные операции над векторами
2. Векторный базис в пространстве n-измерений. Условия существования базиса.
3. Прямоугольный декартов базис. Координаты вектора в этом базисе. Модуль вектора.
4. Направляющие косинусы. Единичный вектор (орт).
5. Скалярное произведение векторов. Определение. Свойства. Вычисление.
6. Векторное произведение векторов. Определение. Свойства. Вычисление.
7. Смешанное произведение векторов. Определение. Свойства. Вычисление.
8. Уравнения прямой на плоскости: с направляющим вектором, через две точки, в «отрезках на осях», с угловым коэффициентом. Общее уравнение прямой.

9. Канонические уравнения и характеристики кривых второго порядка

 

Министерство образования и науки РФ

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

 

 

Направление подготовки 140400.62

«Электроэнергетика и электротехника»

 

МАТЕМАТИКА

 

Самостоятельная работа

 

РГР № 9 (0,278 ЗЕ)

 

Поверхности второго порядка, плоскости и прямые в пространстве

 

 

Срок выполнения 13-17 недели

 

 

Выполнил студент группы ЭА- 111

Петров А.В.

 

Работу принял

 

 

 

Кемерово 2011

 

 

Содержание работы

1. Задачи по линейным объектам в пространстве (плоскости, прямые)

2. Выписать канонические уравнения основных поверхностей второго порядка и схематично их построить

3. По приведенным уравнениям поверхностей описать их свойства и схематично построить поверхности

 

Литература [1,7,17]

 

 

Замечания преподавателя.

 

 

1. Найдите угол между прямыми:

 

 

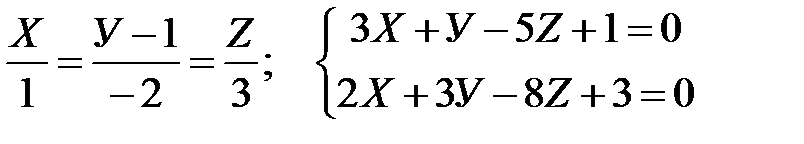
2. Найдите угол между прямой и

плоскостью 4Х–8У+Z–3=0;

 

3. Найдите точку пересечения прямо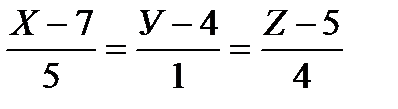й и

плоскости 3Х–У+2Z–5=0

 

4. Запишите уравнение плоскости, проходящей через точку М (3; 4; 1) перпендикулярно прямой Х=5–t; У=4t; Z= -2+t;

 

5. Покажите, что прямые 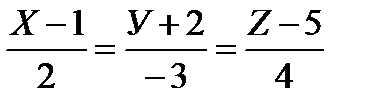и Х=7+3t; У=2+2t; Z=1–2t

лежат в одной плоскости и найдит