Элементы стохастического программирования и теории управления запасами
Отчет о лабораторной работе №5
по курсу “Основы теории принятия решений”
ЯГТУ 220400.62-С8 ЛР
Отчет выполнили
студенты гр. МА-13
____________ А. Ю. Комаров
«___» ____________ 2014
Цель работы
Получение навыка постановки и решения простейшей задачи управления запасами с элементами стохастического программирования, а также анализа оптимального решения задачи.
Условия задачи
Продавец приобретает х единиц продукции (предложение) и продает их. Спрос покупателей – q единиц продукции – случайная величина, распределенная по нормальному закону p(q) (диф. кривая распределения):
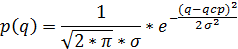
где qcp – средний спрос; σ – среднеквадратичное отклонение, характеризующее разброс (неопределенность) спроса.
В случае если закупка больше спроса (x > q), то остатки продукции на складе будут равны величине (x - q). Если считать стоимость хранения единицы продукции равную с1, то затраты будут вычисляться по выражению:

В случае если закупка меньше спроса (x < q), то величина недопоставки продукции будет равна (q – x). Если считать потери от недопоставки единицы продукции равными c2, то общие потери от недопоставки (штраф за невыполнение контракта на поставку) будет вычисляться по выражению:

Средние убытки от колебания спроса при решении продавца купить x единиц продукции:
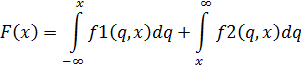
Требуется найти объем закупки продукции, минимизирующий средние убытки продавца.
Исходные данные
σ = 15;
qcp = 230 [единиц];
c1 = 5 [единиц];
c2 = 12 [единиц].
Решение задачи
Формализованная запись задачи
Дифференциальная кривая распределения спроса покупателей:
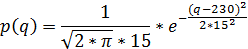
Затраты продавца на хранения излишней продукции:
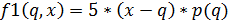
Потери продавца от недопоставки продукции:

И, следовательно, минимизируемые средние убытки продавца:

При ограничениях:


Решим данную задачу в среде MathCad:














3.2 График зависимости средних потерь продавца от объема закупки F(x)



Рис. 1 – График зависимости средних потерь продавца от объема закупки.
Как видно, для построения графика использовался поточечный метод, меняя при этом значение количества приобретаемой продукции x в пределах ± 30 %.
Далее по графику находим объем закупки продукции, минимизирующий средние убытки продавца - 238 [единиц]. И сами убытки – 87.86 [денежных единиц].
Параметрическое исследование задачи
Меняя значения параметров задачи c1, qcp, σ определим зависимость оптимального уровня закупки и средних потерь продавца от данных значений и построим соответствующие таблицы и графики.
4.1 Зависимость от платы за хранения единицы массы запасенного для продажи товара с1
Таблица 1. Зависимость от изменения параметра с1
| c1 | x | F(x) |
| 246.014 | 47.385 | |
| 246.014 | 47.385 | |
| 242.624 | 62.991 | |
| 240.117 | 76.266 | |
| 238.121 | 87.862 | |
| 236.461 | 98.172 | |
| 235.041 | 107.457 | |
| 233.8 | 115.903 | |
| 232.7 | 123.647 |

Рис. 2 – График к таблице 1.
4.2 Зависимость от ожидаемого среднего значения спроса qcp
Таблица 2. Зависимость от изменения параметра qcp
| qcp | x | F(x) |
| 178.121 | 87.862 | |
| 193.121 | 87.862 | |
| 208.121 | 87.862 | |
| 223.121 | 87.862 | |
| 238.121 | 87.862 | |
| 253.121 | 87.862 | |
| 268.121 | 87.862 | |
| 283.121 | 87.862 | |
| 298.121 | 87.862 |

Рис. 3 – График к таблице 2.
4.3 Зависимость от неопределенности спроса σ
Таблица 3. Зависимость от изменения параметра σ
| σ | x | F(x) |
| 231.624 | 17.572 | |
| 233.248 | 35.145 | |
| 234.873 | 52.717 | |
| 236.497 | 70.29 | |
| 238.121 | 87.862 | |
| 239.745 | 105.435 | |
| 241.369 | 123.007 | |
| 242.993 | 140.58 | |
| 244.618 | 158.152 |

Рис. 4 – График к таблице 3.
5 Выводы о влиянии параметров задачи на её оптимальное решение
Из таблицы 1 и соответствующего ей графика видно, что платы за хранения единицы массы запасенного для продажи товара с1 однозначно приводит к уменьшению количества закупаемой продукции x во избежание больших денежных расходов на хранения. Зависимость с1 от F(x) примерно обратно пропорциональная и, следовательно, среднее значение убытков F(x) повышается, что означает, что продавцу следует закупать количество продукции не выше среднего спроса.
Рис. 3 показывает, что увеличение (уменьшение) среднего спроса qcp влияет лишь на объем закупаемой продукции. Средние убытки F(x) при этом несут постоянный характер. Из этого следует, что величина среднего спроса qcp никак не влияет на изменение дохода.
Теперь, если мы проанализируем отклонение, характеризующее неопределенность спроса σ, то по графику, соответствующему таблице 3, можно сказать, что при увеличении отклонения σ средние убытки F(x) и количество продукции x увеличиваются пропорционально друг другу. Поэтому при достаточных величинах неопределенности спроса σ продавец понесет убытки либо из-за недопоставки с2, либо чрезмерной закупки продукции с1.






