Процесса истечения
С процессами истечения, т.е. движения газа, пара или жидкости по каналам различного профиля, в технике приходится встречаться часто. Основные положения теории истечения используются при расчетах различных каналов теплоэнергетических установок: сопловых и рабочих лопаток турбин, регулирующих клапанов, расходомерных сопл и т.п.
В технической термодинамике рассматривается только установившийся, стационарный режим истечения. В таком режиме все термические параметры и скорость истечения остаются неизменными во времени в любой точке канала. Закономерности истечения в элементарной струйке потока переносятся на все сечение канала. При этом для каждого поперечного сечения канала принимаются усредненные по сечению значения термических параметров и скорости, т.е. поток рассматривается как одномерный.
К основным уравнениям процесса истечения относятся следующие:
Уравнение сплошности или неразрывности потока для любого сечения канала
Gv=fc, (1)
где G - массовый расход в данном сечении канала, кг/с,
v - удельный объем газа в этом сечении, м3/кг,
f - площадь поперечного сечения канала, м2,
с - скорость газа в данном сечении, м/с.
Первый закон термодинамики для потока
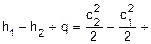l т, (2)
где h1 и h2 - энтальпия газа в 1 и 2 сечениях канала, кДж/кг,
q - теплота, подведенная к потоку газа на интервале 1 и 2 сечений канала, кДж/кг,
c2 и c1 - скорость потока во 2 и 1 сечениях канала, м/с,
l т - техническая работа, совершаемая газом в интервале 1 и 2 сечений канала, кДж/кг.
В данной лабораторной работе рассматривается процесс истечения газа через сопловой канал. В сопловом канале газ не совершает технической работы (l т=0), а сам процесс быстротечен, что обусловливает отсутствие теплообмена газа с окружающей средой (q=0). В результате этого выражение первого закона термодинамики для адиабатного истечения газа через сопло имеет вид
. (3)
Исходя из выражения (3) получаем уравнение для расчета скорости в выходном сечении сопла
. (4)
В экспериментальной установке начальную скорость истечения газа принимают равной нулю (с1=0), ввиду ее очень малого значения по сравнению со скоростью в выходном сечении сопла. Свойства газа при атмосферном давлении или меньше его подчиняются уравнению Pv=RT, а адиабата обратимого процесса истечения газа соответствует уравнению РvК=const с постоянным коэффициентом Пуассона.
В соответствии с вышеизложенным уравнение скорости истечения газа на выходе из соплового канала (4) может быть представлено выражением
. (5)
В выражении (5) индексами "o" обозначены параметры газа на входе в сопло, а индексами "к" - за соплом.
Используя уравнения: неразрывности потока (1), процесса адиабатного истечения газа PvК=const, и уравнение для расчета скорости истечения (5), можно получить выражение для расчета расхода воздуха через сопло
, (6)
где f1 - площадь выходного сечения сопла.
Определяющей характеристикой процесса истечения газа через сопло является величина отношения давлений ε=РК/РО. При давлениях за соплом меньше критического в выходном сечении суживающегося сопла или в минимальном сечении комбинированного сопла давление остается постоянным и равным критическому. Определить критическое давление можно по величине критического отношения давлений εКР=РКР/РО, которое для газов рассчитывается по формуле
. (7)
Используя величины εКР и РКР, можно оценить характер процесса истечения и выбрать профиль соплового канала:
при ε > εКР и РК > РКР истечение докритическое, сопло должно быть суживающимся;
при ε < εКР и РК < РКР истечение сверхкритическое, сопло должно быть комбинированным с расширяющейся частью (сопло Лаваля);
при ε < εКР и РК < РКР истечение через суживающееся сопло будет критическим, в выходном сечении сопла давление будет критическим, а расширение газа от РКР до РК будет происходить за пределами соплового канала.
В режиме критического истечения через суживающееся сопло при всех значениях РК < РКР давление и скорость в выходном сечении сопла будут критическими и неизменными, соответственно, и расход газа через сопло будет постоянный, соответствующий максимальной пропускной способности данного сопла при заданных РО и ТО:
, (8)
, (9)
Увеличить пропускную способность данного сопла возможно только увеличением давления на входе в него. В этом случае происходит увеличение критического давления, что приводит к снижению объема в выходном сечении сопла, а критическая скорость остается неизменной, поскольку она зависит только от начальной температуры.
Действительный - необратимый процесс истечения газа через сопло характеризуется наличием трения, что приводит к смещению адиабаты процесса в сторону увеличения энтропии. Необратимость процесса истечения приводит к увеличению удельного объема и энтальпии в данном сечении сопла по сравнению с обратимым истечением. В свою очередь, увеличение этих параметров приводит к снижению скорости и расхода в действительном процессе истечения по сравнению с идеальным истечением.
Снижение скорости в действительном процессе истечения характеризует скоростной коэффициент сопла φ:
φ = c1i/c1. (10)
Потери располагаемой работы из-за наличия трения в реальном процессе истечения характеризует коэффициент потерь сопла ξ:
ξ = l отр / l о = (hкi-hк)/(hо-hк). (11)
Коэффициенты φ и ζ определяются экспериментально. Достаточно определить один из них, поскольку они взаимосвязаны, т.е. зная один, можно определить другой по формуле
ξ = 1 - φ2. (12)
Для определения действительного расхода газа через сопло используется коэффициент расхода сопла μ:
μ = Gi/Gтеор, (13)
где Gi и Gтеор - действительный и теоретический расходы газа через сопло.
Коэффициент μ определяется опытным путем. Он позволяет, используя параметры идеального процесса истечения, определить действительный расход газа через сопло:
. (14)
В свою очередь, зная коэффициент расхода μ, можно рассчитать коэффициенты φ и ξ для истечения газа через сопло. Записав выражение (13) для одного из режимов истечения газа через сопло, получим соотношение
. (15)
Отношения скоростей и объемов в выражении (15) можно выразить через отношение абсолютных температур идеального и реального процессов истечения
. (16)
где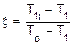 
, подставив его в выражение скоростного коэффициента, получим соотношение
. (17)
Подставив выражения (16) и (17) в формулу (15), получим уравнение
. (18)
В уравнении (18) одна неизвестная величина T1i, которая может быть найдена как один из корней квадратного уравнения, полученного из выражения (18):
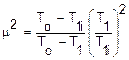. (18а)
Преобразовав выражение (а) и введя константу А, получим квадратное уравнение вида
, (18б)
, (18с)
. (18д)
Корни уравнения (18д) соответствуют выражению
. (18е)
В нашей задаче нужен только положительный корень, т.к. отрицательных абсолютных температур не бывает. Поэтому расчет действительной температуры в конце процесса расширения ведется по выражению
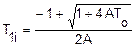. (19)
Скоростной коэффициент сопла φ определяется по выражению (17), используя температуру Т1i, рассчитанную через коэффициент расхода μ по уравнению (19). Коэффициент потерь сопла ξ находится по выражению (12) через скоростной коэффициент φ.
