Экспериментальная установка на «холодном» газе.
Критерии подобия
Опираясь на теорию размерностей и подобия, рассмотрим общую схему построения алгоритма моделирования и создание для этой цели экспериментальной установки. Основные задачи моделирования и создания установки на этом этапе включают:
- Анализ факторов и условий работы РДТТ;
- Выбор общего математического аппарата, описывающего процессы течения газа в камере сгорания, как натурного, так и модельного двигателя;
- Формирование на основании математической модели определяющих параметров и построение базы критериев подобия;
- Определение условий моделирования и построение на основе выбранных объектов подобия математического аппарата, позволяющего вести пересчёт полученных результатов на натурный объект;
- Выбор рабочего тела и условий его подвода к модельному двигателю;
- Моделирование газоприхода с «горящей» поверхности модельного двигателя.
Теория подобия является необходимым инструментом всякого экспериментального исследования. Так как для рассматриваемого процесса движение газа в камере сгорания двигателя полное моделирование невозможно, особое значение имеет выбор состава определяющих критериев и оценка их значимости. Такой состав должен обеспечить достаточно полное моделирование основных свойств потока с помощью относительно простых технических решений.
Смысл моделирования заключается в том, чтобы дать необходимые ответы о характере эффектов и влиянии различных величин, связанных с явлениями в натурных условиях при формировании течения газа в камере сгорания РДТТ. Из теории подобия следует, что два явления подобны, если по заданным характеристикам одного можно получить характеристики другого простым пересчётом, который аналогичен переходу от одной системы единиц измерения к другой, то есть подобными физическими процессами будут такие явления одной природы, которые протекают в геометрически подобных пространственных системах, и, у которых значения переменных, характеризующих одноимённые явления, пропорциональны в сходственных точках и гомохронные моменты времени. Такое преобразование переменных, при котором значение каждой из них меняется в определённое число раз, называется подобным преобразованием. Необходимым и достаточным условием подобия двух явлений является постоянство численных безразмерных комбинаций, образующих базу.
Предположим, что изучаемое явление зависит от n переменных (
). С помощью подобного преобразования, то есть преобразования вида 
каждого из перечисленных переменных, изучаемое явление можно свести к подобному ему явлению. Так, если в любой точке системы значения переменных соответствуют , то в сходной точке подобной ей системы в гомохронный момент времени значения переменных будут соответствовать 
, причём 
, 
,…, 
, где множители подобного преобразования (константы подобия).
Однако не любая совокупность значений множителей сводит изучаемое явление к подобному.
Действительно, так как переменные характеризуют изучаемое явление, то между ними существует связь, которая математически выражается уравнениями (в данном случае уравнениями движения вязкого газа в канале камеры сгорания РДТТ).
Пусть изучаемое физическое явление описывается в общем виде системой уравнений:
(1.1)
Путём преобразования переменных система уравнений (1) для подобного явления будет иметь вид:
(1.2)
Если системы уравнений (1) и (2) описывают подобные явления, то они должны иметь совместное решение. Свойство уравнений оставаться неизменными при каких-либо преобразованиях, входящих в них величин, называется инвариантностью рассматриваемых уравнений относительно произведённых преобразований. Из математики известно, что две системы инвариантны, если множители преобразования выйдут за знак функции (f) системы (2), то есть система преобразуется к виду:
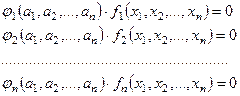(1.3)
Системы уравнений (1) и (2) имеют совместное решение в том случае, если имеет место следующее соотношение:
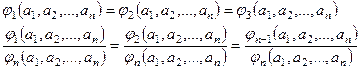(1.4)
Соотношение (3) обуславливает инвариантность уравнений системы (2) относительно подобного преобразования входящих в них переменных () и носит название обуславливающих уравнений. Следовательно, между множителями подобного преобразования существует связь, которая может быть описана следующими теоремами подобия, (?).
Первая теорема подобия гласит: «У подобных явлений, описываемых уравнениями, их инварианты относительно подобных преобразований, входящих в эти уравнения переменных параметров одинаковы.» На выбор совокупности множителей подобного преобразования не влияет количество рассматриваемых параметров, описывающих процесс.
Исходная система уравнений пригодна для описания бесконечного множества явлений одной и той же природы. Конкретное явление может быть выделено из класса явлений, задаваемых условием однозначности. Задание условия однозначности включает:
- геометрические особенности: форма ограничивающих поверхностей или пространства, их размер, в котором осуществляется тот или иной процесс;
- особенности протекания процесса во времени;
- начальные условия, определяющие распределение по пространству определяющих величин: давления, плотности газа, скорости, температуры и пр.;
- граничные особенности, включающие распределение по границам определяющих параметров (массоприход, давление вдува и пр.).
- физические и химические особенности среды, в которой осуществляется процесс.
Математический аппарат вопросов о единстве решений составленных уравнений и присоединенных к ним условий однозначности часто бывает чрезвычайно сложным, поэтому обычно исходя при этом из соображений физического характера изучаемого процесса.
В теории подобия вводится понятие группы подобных явлений, в пределах которой можно производить обобщение экспериментальных данных. Первая теорема подобия устанавливает необходимый признак существенных явлений, относящихся к одной группе. Если обуславливающие уравнения вместо множителей подобного преобразования поставить их выражение через переменные, то необходимые условия существования группы подобных явлений можно записать следующим образом:
k1=i dem, k2=i dem,…, kn=i dem.
Где ki - безмерные величины, составленные из переменных , называемые критериями подобия.
Вторая теорема подобия утверждает, что «уравнения, выражающие связь между переменными могут быть преобразованы в уравнение связи между критериями.»
Критерии подобия, выделенные из исходных уравнений можно разбить на две категории. К первой категории критериев подобия, называемых определенными, относят такие критерии, которые составлены только из величин входящих в условия однозначности. Если же выражения для критерия имеет хотя бы одну из переменных, не входящих в условие однозначности, то такой критерий называют неопределяющим.
Первые две теоремы подобия исходят из существования подобия, как известного фактора, который наперед задан. Третья теорема наоборот, устанавливает признаки, по которым можно узнать подобны ли два явления друг другу. Она гласит: «Равенство определяющих критериев подобия, наряду с подобием условий однозначности и инвариантности исходных уравнений, необходимо и достаточно для подобия рассматриваемых явлений.»
Таким образом, третья теорема подобия указывает каким образом практически можно осуществить подобные явления, что бы результаты экспериментов были справедливы для явлений одной группы.
Пользуясь второй и третьей теоремами подобия критериев, можно показать что каждый из неопределяющих критериев подобия есть однозначная функция совокупности всех определяющих критериев подобия.
Для составления базы определяющих критериев рассмотрим неустановившееся турбулентное движение вязкого газа в осесимметричном канале сложной формы с газоприходом с его боковых поверхностей и истечение его через критическое сечение сопла. В общем случае при изучении неустановившегося движения газа мы должны вводить в число определяющих параметров время (τ), являющихся переменной величиной. При рассмотрении механизма подобных движений мы встречаемся с изменением численного значения параметра – времени (τ) за счет изменения масштаба и за счет изменения времени процесса движения. В связи с этим мы остановимся на некоторых общих значениях, связывающих кинематически подобные неустановившиеся движения.
Пусть мы имеем неустановившиеся кинематически подобные движения, представляющие течение вязкого газа. Система уравнений, описывающих этот процесс включает полные уравнения Новье-Стокса, уравнение состояния, уравнение энергии и уравнение связи.(?)
Для определения акустических возмущений, связанных с движением и обтеканием элементов рабочего тракта РДТТ, уравнение сохранения количества движения можно рассматривать как совокупность двух уравнений – стационарного, или невозмущённого, и пульсационного. Решение пульсационного уравнения для продольных колебаний газа в стационарном потоке можно представить в виде:
(1.5)
С учётом уравнения для акустического давления (1.5) система определяющих параметров для такого потока в канале камеры сгорания РДТТ и модельного двигателя будет состоять из следующих величин:
(1.6)
Состояние движений систем в каждый момент времени определяется начальными возмущениями (возмущения газа в момент времени τ=0) и свойствами инерции газа, то есть величинами: плотностью (ρ) и вязкого газа (μ).
На основе анализа условий моделирования газодинамических процессов в камере сгорания РДТТ, размерные определяющие параметры (1.6) могут быть выражены критериями подобия:
(1.7)
На основании второй и третьей теоремы теории подобия рассматриваемые процессы течения газа в камере сгорания РДТТ будут подобны, если будут выражены условия равенства критериев (1.7):
(1.8)
При этом критерии: геометрический (
) и гомохронный (
) должны не зависеть от изменения координат и времени, то есть:
Рассмотрим совокупную базу критериев подобия (1.7), моделирование процессов течения газа в камере сгорания РДТТ и условия их соблюдения.
Для механических систем принято разделение безразмерных критериев на группы, отличающиеся по функциональному назначению. Различают линейное и геометрическое, гомохронное или временное подобие. Эта группа критериев относится к обязательным условиям выполнения при моделировании и характеризуется масштабом соответствующих величин, то есть необходимым и достаточным условием соблюдения указанных критериев является постоянство отношений их одноимённых величин:
(1.9)
(1.10)
В группе критериев выделяется кинематическое подобие, которое связывает в сходных точках соответствующих потоков их абсолютные скорости:
(1.11)
Применительно к моделированию газодинамических процессов в камере РДТТ к группе кинематических критериев подобия можно отнести коэффициент инвариантности по скорости чисел Маха (М) и Струхаля (Sh). Их выражения можно записать:
Коэффициент инвариантности (
) необходимо отнести к термодинамическим параметрам, т.к. скорость звука в газовом потоке определяется через параметры газа:
К сложным критериям подобия относятся динамические (Re, q) и термодинамические (γ, Pr), (1.7). Под динамическим подобием понимается такое подобие, при котором соблюдается подобие многоугольников всех сил, действующих в геометрически подобных точках пространства или тела. Условие динамического подобия в общем виде запишется:
(1.12)
Термодинамическое подобие – это подобие, при котором в газовом потоке в геометрически подобных точках пространства соблюдается постоянное соотношение относительного изменения величины полной энергии:
(1.13)
Подобие называется полным, если во всем пространстве определяющем соответствующие сравниваемые процессы, выполняются постоянными соотношениями вышеперечисленные критерии, т.е.:
Если хотя бы одно из условий равенства критериев подобия системы (1.7) будет не соблюдено, т.е. при переходе из одной исследуемой зоны в камере сгорания РДТТ в другую параметры изменяются на постоянную и известную величину, то такое моделирование называют частичным:
.
К условному подобию прибегают, когда при постановке опытов не представляется возможным применить даже частичное подобие. В этом случае коэффициент инвариантности критериальных чисел будет переменной величиной, зависящей как от координаты, так и от времени:
.
Выбор схемы и параметров экспериментальной установки.
Разнообразие форм проточной части камеры сгорания РДТТ и широкий диапазон их рабочих характеристик, приводит к необходимости формирования общих требований, которые должны быть реализованы при выборе схемы и параметров экспериментальной установки.
Установка должна обеспечить:
- Геометрическое подобие проточной части камеры широкого класса РДТТ;
- Вариацию расходных характеристик и давление в камере сгорания модельного двигателя;
- Формирование потока газа в камере сгорания модельного двигателя экспериментальной установки в каждом случае конкретного РДТТ;
- Получение достоверной информации о процессах течения газа в камере сгорания;
- Необходимость мобильного изменения геометрии и параметров рабочего тела при проведении исследований.
В результате анализа работы широкого круга крупногабаритных РДТТ (9Д128, 9Д140, SRM и др.) получены интервалы изменения геометрических параметров газового тракта и рабочего тела, используемого для осуществления продувки в экспериментальной установке:
- По геометрическому критерию () от 1⁄5 до 1⁄20;
- По величине расхода рабочего тела (Ġ) 0÷0,6 кг⁄сек;
- По давлению продувки (Рк) 0,2÷0,3 МПа;
- По амплитуде внешнего акустического поля (А) 100-130dВ;
- По замеряемым параметрам акустического шума по амплитуде (А) от 60 до 200dВ и по частоте (f) от 100 до 200 Гц.
Реализация требуемых параметров моделирования процессов горения газа в камере сгорания РДТТ позволила создать экспериментальную установку на основе модульной схемы.
Схема экспериментальной установки
Рис.2.1
Принципиальная система экспериментальной установки приведена на рис.2.1. Кратко остановимся на описании каждой из систем, входящей в структурную схему установки.
Основным её элементом является модельный двигатель, предназначенный для:
- Формирования в соответствии с теорией подобия конструктивной формы проточной части камеры сгорания РДТТ;
- Осуществления газоприхода с «горящей» поверхности камеры сгорания и формирования потока по её проточной части;
- Регистрации параметров акустического поля, создаваемого потоком;
- Управления акустическим полем.
Для осуществления продувки модельного двигателя экспериментальной установки разработана система подачи рабочего тела. Она предназначена для хранения рабочего тела и гарантийного обеспечения в заданных пределах его подвод к модельному двигателю. Схема системы приведена на рис.2.2.
(Пневмосхема экспериментальной установки «ЭХО»)
В состав системы входят: компрессор, рампа из 6 баллонов, система трубопроводов высокого (25 МПа) и низкого (до 0,6 МПа) давления. Для избежания ударов при включении отсечного клапана на редукторах и модельном двигателе в системе подвода предусмотрены ресиверы высокого и низкого давления. Магистраль низкого давления содержит механический дроссель, позволяющий создать пульсации расхода рабочего тела с частотой до f =1000 Гц, и 4 резиновых шланга для соединения с модельным двигателем.
Система управления подачей рабочего тела предназначена осуществлять по команде системы управления включение и отключение подачи рабочего тела. На рис.2. приведена пневмосхема системы управления подачей рабочего тела. Система имеет автономный источник питания сжатым воздухом – 40-литровый баллон. Управление пневмоцилиндром отсечного клапана осуществляется подачей воздуха под давлением Р=5МПа одним из электропневмоклапанов (ЭПК), работающих в режиме включения
Измерительно-задающий комплекс с системой единого времени предназначен для управления исследовательским процессом во времени, задания детерминированного внешнего акустического воздействия на газовый поток в камере сгорания модельного двигателя, регистрации возникающего при этом акустического поля потока, обрабоки и представления результатов исследования. Система единого времени в соответствии с заложенной программой обеспечивает включение и отключение всех систем экспериментальной установки. Основные характеристики измерительно-задающего комплекса приведены в таблице 2.1.
Измерение параметров газового потока по его акустической картине производится пятью датчиками, регистрируется с записью на магнитную ленту. Предварительный анализ производится на осциллографе, а полный – спектранализаторе. Анализ и обработка результатов исследований включает в себя:
- Спектральный анализ акустического поля камеры сгорания по каждому каналу записи;
- Качественный и количественный анализ сигналов с выявлением несущих амплитуд и уровней давления на этих частотах;
- Интегральная оценка уровня общего шума в камере сгорания.
Для проведения спектрального анализа результатов записи акустического шума в камере сгорания был использован анализатор 2034 фирмы «Брюль и Къер» (Дания), а запись результатов проводилась с помощью графического регистратора 2313 этой же фирмы и самописца фирмы «Роботрон» (ГДР).
Конструктивно, элементы экспериментальной установки размещены на раме, позволяющей свободный доступ к любому элементу системы. Для обеспечения безопасного проведения работ и избежания воздействия на человека высокоскоростной струи, воздух после продувки отводится в безопасную зону с помощью отводной магистрали.
Основные характеристики экспериментальной установки сведены в таблицу 2.1.
Таблица 2.1.
| № | Наименование характеристики | Обозначение | Размерность | Величина | Примечание |
| Задаваемые параметры газового потока | |||||
| Давление хранения воздуха | Р | МПа | 18÷25 | ||
| Давление редуцирования | Р | МПа | 0,3÷0,6 | ||
| Давление продувки | Р | МПа | 0,2 | ||
| Расход воздуха | Ġ | кг⁄с | до 0,66 | ||
| Температура рабочего тела | Т | 0С | -30÷+30 | ||
| Частота пульсаций в потоке на входе в модельный двигатель | f | Гц | 0÷1000 | ||
| Характеристики внешнего акустического источника | |||||
| Частота | f | Гц | 100÷2000 | ||
| Амплитуда | А | дБ | 40÷130 | ||
| Регистрируемые характеристики акустического поля | |||||
| Частота | f | Гц | 22÷34000 | ||
| Амплитуда | А | дБ | 40÷200 | ||
| Погрешность регистрации по частоте | % | ||||
| Погрешность записи по амплитуде | Δ | % | |||
| Число каналов записи | n | шт | |||
| Число каналов одновременной обработки на анализаторе | n | шт | |||
| Фиксация результатов обработки | Бумажная лента, спектрограммы | ||||
| Полоса пропускания анализатора | f | Гц | |||
| Интегральная оценка шума | ИВШ-1 | дБ | |||
| Уровень обработки сигнала | В | В | до 1 | ||
| Полоса просмотра по амплитуде | А | дБ | |||
| Чувствительность датчика акустического давления | А | мВ⁄дБ | 0,04 | ||
| Входное сопротивление | R | КОм | |||
| Динамический диапазон | Δf | Гц | 100÷14000 | ||
| Собственные частоты | f | Гц | |||
| Условия работы и диапазоны потребляемых мощностей | |||||
| Напряжение питания ИЗК | U | В | |||
| Потребляемая мощность | N | кВт | 1,3 | ||
| Напряжение в системе управле-ния подачи рабочего тела | U | В | +27 | ||
| Давление управления в системе подачи рабочего тела | Р | МПа | 5,0 | ||
| Время проведения эксперимента (один цикл) | τ | с | |||
| Время продувки | τ | с |
