Задача 5. Дана однородная линейная система уравнений. Найти множество решений системы, исследовав ее на совместность через определители

Расчетно-графическая работа №1

«Элементы линейной алгебры»

Задача 1. Найти , если:

1.1. , 1.16. ,

1.2. , 1.17. ,

1.3. , 1.18. ,

1.4. , 1.19. ,

1.5. , 1.20. ,

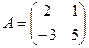
1.6. , 1.21. ,

1.7. , 1.22. ,

1.8. , 1.23. ,

1.9. , 1.24. ,

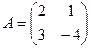
1.10. , 1.25. ,

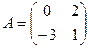
1.11. , 1.26. ,

1.12. , 1.27. ,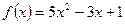

1.13. , 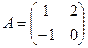1.28. ,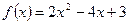

1.14. , 1.29. ,

1.15. , 1.30. ,

 

2. Вычислить определитель, пользуясь свойствами определителей:

2.1.

2.2.

2.3.

2.4.

2.5.

2.6.

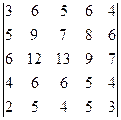
2.7.

2.8.

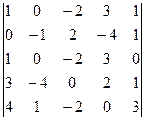
2.9.

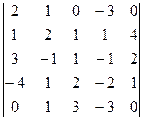
2.10.

2.11.

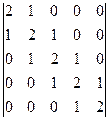
2.12.

2.13.

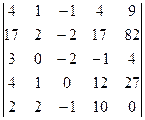
2.14.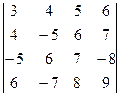

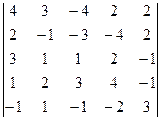
2.15.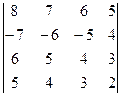

2.16.

2.17.

2.18.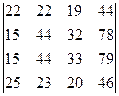

2.19.

2.20.

2.21.

2.22.

2.23.

2.24.

2.25.

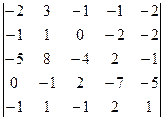
2.26.

2.27.

2.28.

2.29.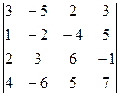

2.30.

Задача 3. Дана линейная неоднородная система уравнений. Исследовать систему на совместность тремя способами и решить ее:

По формулам Крамера

Матричным методом

Методом Гаусса

3.1 а) 3х₁-х₂+4х₃=4 б) 2х₁-5х₂-6х₃=5

2х₁+3х₂-х₃=-1 -3х₁+2х₂+5х₃=1

7х₁+2х₂-2х₃=-9 2х₁+4х₂-3х₃=-16

 

3.2 а) -2х₁+3х₂+х₃=14 б) 2х₁+х₂+3х₃=-9

2х₁+5х₂-3х₃=8 8х₁+3х₂+5х₃=-13

3х₁-4х₂+2х₃=-16 2х₁+5х₂-х₃=-5

 

3.3 а) х₁-5х₃=8 б) 5х₁-9х₂+4х₃=7

х₁-3х₂-2х₃=-1 7х₁-3х₂+5х₃=32

2х₁-х₂-6х₃=7 2х₁+4х₂+3х₃=41

3.4 а) 7х₂-2х₃=-8 б) 2х₁-х₂+х₃=4

5х₁-6х₂+4х₃=20 4х₁+х₂-2х₃=0

6х₁+4х₂+3х₃=7 х₁-3х₂+х₃=3

 

3.5 а) 4х₁-12х₃+13х₃=27 б) 2х₁-х₂-х₃=4

11х₁-7х₂+9х₃=20 3х₁+4х₂-2х₃=11

15х₁-12х₂+17х₃=39 3х₁-2х₂+4х₃=11

 

3.6 а) 3х₁+8х₂-х₃=34 б) 3х₁+2х₂+х₃=5

6х₁+4х₂+х₃=17 2х₁+3х₂+х₃=1

16х₁+13х₂+х₃=52 2х₁+х₂+3х₃=11

 

3.7 а) 2х₁-3х₂+х₃=10 б) х₁+2х₂+4х₃=31

х₁+х₂=2 5х₁+х₂+2х₃=29

х₁-х₂+х₃=5 3х₁-х₂+х₃=10

 

3.8 а) 4х₁-5х₂+5х₃=18 б) 2х₁+3х₂+5х₃=10

5х₁+х₂-х₃=8 3х₁+7х₂+4х₃=3

6х₁-4х₂+3х₃=21 х₁+2х₂+2х₃=3

 

3.9 а) 5х₁-6х₂-3х₃=16 б) 5х₁-6х₂+4х₃=3

7х₁-9х₂-4х₃=22 3х₁-3х₂+2х₃=2

11х₁-14х₂-6х₃=35 4х₁-5х₂+2х₃=1

 

3.10 а) 2х₁-4х₂+7х₃=45 б) 4х₁-3х₂+2х₃+4=0

4х₁-2х₂+3х₃=23 6х₁-2х₂+3х₃+1=0

7х₁-3х₂+8х₃=53 5х₁-3х₂+2х₃+3=0

 

3.11 а) 4х₁+2х₂+5х₃=15 б) 5х₁+2х₂+3х₃=0

5х₁+х₂+х₃=8 2х₁-2х₂+5х₃=0

х₁+3х₂-2х₃=-15 3х₁+4х₂+2х₃+10=0

3.12 а) 2х₁+3х₂+х₃=10 б) 3х₁-3х₂+2х₃=2

3х₁-2х₂-2х₃=-4 4х₁-5х₂+2х₃=1

8х₁-х₂+5х₃=-14 5х₁-6х₂+4х₃=3

 

3.13 а) 3х₁+8х₂-х₃=34 б) 3х₁+2х₂-4х₃=8

6х₁+4х₂+х₃=17 2х₁+4х₂-5х₃=11

16х₁+13х₂+х₃=52 4х₁-3х₂+2х₃=1

 

3.14 а) 2х₁-х₂-х₃=4 б) 2х₁-х₂+4х₃=15

3х₁+4х₂-2х₃=11 3х₁-х₂+х₃=8

3х₁-2х₂+4х₃=11 -2х₁+х₂+х₃=0

 

3.15 а) х₁+х₂+2х₃=-1 б) х₁+х₂+х₃=1

2х₁-х₂+2х₃=-4 х₁-х₂+2х₃=-5

4х₁+х₂+4х₃=-2 4х₁+х₂+4х₃= -2

 

3.16 а) 3х₁-х₂+4х₃=4 б) 2х₁+х₂-х₃-2=0

2х₁+3х₂-х₃=-1 3х₁+х₂-2х₃-3=0

7х₁+2х₂-2х₃=-9 х₁+х₃-3=0

3.17 а) 2х₁+2х₂-х₃=-2 б) 2х₁+3х₂-х₃=4

3х₁-3х₂+4х₃=2 х₁+х₂+3х₃=5

х₁+4х₂+х₃=5 3х₁-4х₂+х₃=0

3.18 а) 2х₁-3х₂+4х₃=1 б) 3х₁+2х₂+х₃=5

х₁+2х₂-3х₃=2 х₁+х₂-х₃=0

3х₁-х₂+2х₃=2 4х₁-х₂+5х₃-3=0

 

3.19 а) 2х1-3х2+х₃=-9 б) 3х₁+5х₂+7х₃=6

5х₁-10х₂+3х₃+31=0 2х₁+3х₂+5х₃=3

4х₁+2х₂+х₃-8=0 х₂+3х₃=-1

 

3.20 а) 3х₁-х₂+4х₃-10=0 б) 2х₁+х₂-х₃=5

2х₁+3х₂-х₃-3=0 х₁-2х₂+2х₃=-5

х₁-4х₂+2х₂-1=0 7х₁+х₂-х₃=10

 

3.21 а) 3х₁-2х₂+4х₃-11=0 б) х₁+2х₂+3х₃=14

2х₁+х₂-3х₃+5=0 х₁+х₂+х₃=6

4х₁+2х₂+х₃-11=0 х₁+х₂=3

 

3.22 а) 5х₁-6х₂+4х₃-3=0 б) х₁+2х₂+х₃=6

3х₁-3х₂+2х₃-2=0 3х₁-х₂+2х₃=3

4х₁-5х₂+2х₃-1=0 5х₁+2х₂+х₃=10

 

3.23 а) 2х₁-х₂+х₃=0 б) 2х₁+4х₂+х₃=0

3х₁-2х₂-х₃-5=0 3х₁+2х₂+2х₃=5

х₁+х₂+х₃-6=0 2х₁+5х₂+х₃=-1

3.24 а) х₁+х₂-х₃=6 б) 2х₁+3х₂+2х₃-6=0

2х₁+3х₂-4х₃=21 4х₁+2х₂+5х₃-5=0

7х₁-х₂-3х₃=6 х₁+2х₂+х₃-4=0

 

3.25 а) 2х₁+х₂-2х₃=6 б) х₁+2х₂-х₃-2=0

х₁+2х₂+3х₃=2 2х₁-3х₂+2х₃-2=0

х₁-х₂+х₃=-2 3х₁+х₂+х₃-8=0

 

3.26 а) 2х₁+3х₂+5х₃=10 б) х₁+2х₂-10=0

3х₁+7х₂+4х₃-3=0 3х₁+2х₂+х₃-23=0

х₁+2х₂+2х₃-3=0 х₂+2х₃-13=0

 

3.27 а) 4х₁-3х₂+2х₃+4=0 б) 2х₁-3х₂+4х₃=4

6х₁-2х₂+3х₃+1=0 3х₁+2х₂-х₃=-2

5х₁-3х₂+2х₃+3=0 х₁-3х₂+2х₃=-1

 

3.28 а) х₁-2х₂+3х₃+2=0 б) 3х₁+2х₂-х₃=3

2х₁+3х₂-х₃-3=0 2х₁-х₂+2х₃=5

3х₁-х₂+2х₃+3=0 5х₁+3х₂-3х₃=2

 

3.29 а) 3х₁+х₂-4х₃-5=0 б) 2х₁-3х₂+6х₃=17

х₁+2х₂+х₃-5=0 3х₁+4х₂-х₃=-3

2х₁-3х₂+2х₃+4=0 х₁-5х₂+2х₃=10

 

3.30 а) 5х₁+2х₂+3х₃=-2 б) 2х₁-х₂+3х₃-2=0

2х₁-2х₂+5х₃=0 х₁+2х₂-х₃-1=0

3х₁+4х₂+2х₃+10=0 3х₁+х₂+х₃-4=0

 

3.31 а) 7х₁+2х₂+3х₃=15 б) х₁+х₂-2х₃=6

5х₁-3х₂+2х₃=15 х₁+х₂-2х₃=6

10х₁-11х₂+5х₃=36 5х₁+2х₂+х₃=16

 

3.32 а) 5х₁+8х₂+х₃=2 б) 2х₁-3х₂+х₃=-7

3х₁-2х₂+6х₃=-7 х₁+4х₂+2х₃=-1

2х₁+х₂-х₃=-5 х₁-4х₂=-5

 

Задача 4. Исследовать каждую из указанных систем и в случае совместности решить ее любым методом.

4.1 а) 3х₁+4х₂-х₃=7 б) 3х₁+2х₂-3х₃=-3

х₁+2х₂-3х₃=0 х₁+2х₂+4х₃=9

7х₁+10х₂-5х₃=2 2х₁+7х₂-х₃=0

3х₁+8х₂-х₃=1

 

4.2 а) 5х₁+8х₂+3х₃=11 б) 2х₁-3х₂-х₃=2

х₁+3х₂+2х₃=5 3х₁+4х₂+х₃=7

3х₁+2х₂-х₃=1 7х₁-2х₂+х₃=0

х₁+х₂=1

 

4.3 а) 3х₁-2х₂-3х₃=5 б) 3х₁+2х₂-3х₃+4х₄=1

х₁-3х₂+4х₃=1 2х₁+3х₂-2х₃+3х₄=2

7х₁-7х₂-2х₃=0 4х₁+2х₂-3х₃+2х₄=3

 

4.4 а) 2х₁+3х₂-х₃+х₄=2 б) 2х₁+3х₂=-1

7х₁-2х₂+х₄=3 3х₁+4х₂=-1

3х₁+х₂+х₃-2х₄=7 7х₁-х₂=6

3х₁-8х₂+2х₃-х₄=5 5х₁+3х₂=2

 

4.5 а) 2х₁+х₂-х₃=5 б) х₁+х₂-3х₄-4х₅=0

х₁-3х₂+3х₃=7 х₁+х₂-х₃+2х₄-х₅=1

5х₁-3х₂+3х₃=7 2х₁+2х₂+х₃-х₄+3х₅=0

 

4.6 а) 2х₁+3х₂-5х₃+х₄-х₅=0 б) х₁-х₂=3

х₁+2х₂+3х₃+2х₄+2х₅=3 2х₁+4х₂=12

4х₁+7х₂+х₃+5х₄+3х₅=1 7х₁-5х₂=23

5х₁+9х₂+4х₃+7х₄+5х₅=8

 

4.7 а) 2х₁-3х₂+4х₃-х₄=-3 б) х₁+х₂-3х₃=-1

3х₁-2х₂-х₃+3х₄=0 2х₁+х₂-2х₃=1

х₁+3х₂-4х₃+5х₄=8 х₁+х₂+х₃=3

х₁+2х₂-3х₃=1

 

 

4.8 а) х₁+4х₂-3х₃+2х₄=4 б) 2х₁+х₂+х₃=2

2х₁-х₂-х₃+3х₃=2 х₁+3х₂+х₃=5

3х₁+2х₂+х₃-2х₄=-4 х₁+х₂+5х₃=-7

2х₁+3х₂-3х₃=14

 

4.9 а) 3х₁-2х₂-х₃+2х₄=-2 б) х₁-2х₂+х₃=1

2х₁-4х₂+3х₃-х₄=-5 2х₁+3х₂-х₃=1

х₁+х₂-2х₃+3х₄=4 4х₁-х₂+х₃=1

 

4.10 а) х₁-2х₂+3х₃-х₄=-2 б) 2х₁-х₂+3х₃=4

4х₁+х₂-х₃+2х₄=0 х₁+2х₂+2х₃=-1

3х₁-2х₂+2х₃+х₄=-1 4х₁+3х₂+7х₃=3

 

4.11 а) 2х₁+3х₂-х₃=1 б) 2х₁-3х₂+4х₃-х₄=1

3х₁-2х₂+3х₃=0 2х₁-3х₂+2х₃+3х₄=2

х₁+3х₂+2х₃=5 2х₁-3х₂+2х₃-11х₄=-4

3х₁+2х₂+2х₃=3

 

4.12 а) х₁-х₂+2х₃-х₄=1 б) х₁-2х₂+3х₃=4

х₁-х₂+х₃-х₄=0 2х₁-3х₂+х₃=2

х₁-х₂+5х₃-х₄=4 х₁+х₂-2х₃=-1

х₁-х₂+6х₃-х₄=5 3х₁-3х₂+4х₃=6

 

4.13 а) 4х₁+3х₂-3х₃-х₄=4 б) 3х₁+4х₂-2х₃=11

3х₁-х₂+3х₃-2х₄=1 2х₁-х₂-х₃=4

3х₁+х₂-х₄=0 3х₁-2х₂+4х₃=11

5х₁+4х₂-2х₃+х₄=3 х₁+5х₂-х₃=7

 

4.14 а) 4х₁+х₂+4х₃=-2 б) х₁+х₂-х₃+х₄=2

2х₁-х₂+2х₃=-4 х₁-х₂+х₃-х₄=0

х₁+х₂+2х₃=-1 2х₁+3х₂+2х₃-3х₄=3

4х₁+х₂+6х₃=-6 х₁-2х₂-3х₃+4х₄=0

 

4.15 а) 2х₁-4х₂+3х₃-2х₄=3 б) х₁+х₂-3х₃=-1

х₁-2х₂-2х₃-х₄=-2 2х₁+х₂-2х₃=-1

3х₁-6х₂+5х₃-3х₄=5 х₁+х₂+х₃=3

4х₁-8х₂-3х₃-4х₄=-3 х₁+2х₂-3х₃=1

4.16 а) 2х₁+х₂+х₃=2 б) 2х₁+х₂-х₃+х₄=1

х₁+3х₂+х₃=5 3х₁-2х₂+2х₃-3х₄=2

х₁+х₂+5х₃=-7 5х₁+х₂-х₃+2х₄=-1

2х₁+3х₂-3х₃=14 2х₁-х₂+х₃-3х₄=4

 

4.17 а) 2х₁-х₂+х₃-х₄=1 б) 3х₁-2х₂+х₃=2

2х₁-х₂-3х₄=2 2х₁+х₂-2х₃=1

3х₁-х₃+х₄=-3 -х₁+3х₂-3х₃=-1

2х₁+2х₂-2х₃+5х₄=-6 х₁+4х₂-5х₃=0

 

4.18 а) х₁-2х₂+3х₃-4х₄=4 б) х₁-2х₂+3х₃=2

х₂-х₃+х₄=-3 2х₁+х₂-х₃=1

х₁+3х₂-3х₃=1 4х₁-3х₂+5х₃=3

-7х₂+3х₃+х₄=-3

 

4.19 а) 2х₁-х₂+3х₃=2 б) 2х₁+х₂+х₄=2

х₁+2х₂-х₃=1 3х₁-х₂-2х₃+3х₄=1

4х₁+3х₂+х₃=1 9х₁+3х₂-х₃+2х₄=2

2х₁+3х₂+2х₃+3х₄=2 4х₁+3х₂+х₃-2х₄=-1

х₁+3х₂+2х₃-х₄=3

 

4.20 а) 2х₁+2х₂+3х₃+2х₄=3 б) 2х₁-3х₂+х₃=2

2х₂+3х₃+2х₄=3 х₁+2х₂-2х₃=1

2х₁+3х₂+2х₃+2х₄=3 4х₁+х₂-3х₃=-1

3х₂+2х₃+2х₄=3

 

4.21 а) 2х₁-3х₂-х₃+2х₄=3 б) 2х₁+5х₂-х₃=-5

3х₁+5х₂+9х₃-4х₄=-8 8х₁+3х₂+5х₃=-13

4х₁-3х₂+5х₃+7х₄=14 2х₁+х₂+3х₃=-9

х₁-2х₂+х₃=2

 

4.22 а) х₁+х₂+х₃+х₄+х₅=7 б) 2х₁-3х₂+х₃=1

3х₁+2х₂+х₃+х₄-3х₅=-2 х₁+2х₂-2х₃=3

х₂+2х₃+2х₄+6х₅=23 4х₁+х₂-3х₃=4

5х₁+4х₂+3х₃+3х₄-х₅=12

 

 

4.23 а) 2х₁+х₂-х₃-х₄+х₅=1 б) 3х₁-2х₂+х₃=2

х₁-х₂+х₃+х₄-2х₅=0 х₁+х₂-2х₃=1

3х₁+3х₂-3х₃+3х₄+4х₅=2 5х₁-3х₂=-2

4х₁+5х₂-5х₃-5х₄+7х₅=3

 

4.24 а) 2х₁-2х₂+х₃-х₄+х₅=1 б) 2х₁-3х₂+4х₃=2

х₁+2х₂-х₃+х₄-2х₅=1 х₁+2х₂-2х₃=1

4х₁-10х₂+5х₃-5х₄+7х₅=1 4х₁+х₂=-2

2х₁-14х₂+7х₃-7х₄+11х₅=-1

 

4.25 а) 3х₁+х₂-2х₃-х₄+х₅=1 б) 5х₁-9х₂+4х₃=7

2х₁-х₂+7х₃-3х₄+5х₅=2 7х₁-3х₂+5х₃=32

х₁+3х₂-2х₃+5х₄-7х₅=3 2х₁+4х₂+3х₃=41

3х₁-2х₂+7х₃-5х₄+8х₅=3 х₁-2х₂+х₃=3

 

4.26 а) х₁+2х₂-3х₄+2х₅=1 б) х₁+х₂+х₃=6

х₁-х₂-3х₃+х₄-3х₅=2 2х₁-х₂+х₃=3

2х₁-3х₂+4х₃-5х₄+2х₅=7 х₁-х₂+2х₃=5

9х₁-9х₂+6х₃-16х₄+2х₅=25 3х₁-6х₂+5х₃=6

 

4.27 а) 3х₁+х₂-х₃-х₄=2 б) х₁-х₂+х₃=-2

9х₁+х₂-2х₃-х₄-2х₅=5 2х₁+х₂-2х₃=6

х₁-х₂-х₄+2х₅=1 х₁+2х₂+3х₃=2

х₁+х₂-х₃-3х₄+4х₅=2 3х₁-х₂+2х₃=-1

 

4.28 а) 2х₁+3х₂-х₃=4 б) 2х₁+7х₂+3х₃+х₄=6

х₁+х₂+3х₃=5 3х₁+5х₂+2х₃+2х₄=4

3х₁-4х₂+х₃=0 9х₁+4х₂+х₃+7х₄=2

2х₁+х₂-х₃=2

 

4.29 а) 2х₁-3х₂+5х₃+7х₄=1 б) 2х₁+5х₂-8х₃=8 4.30 а) 3х₁-5х₂+2х₃+4х₄=2 б) х₁-х₂+2х₃-х₄=1

4х₁-6х₂+2х₃+3х₄=2 4х₁+3х₂-9х₃=9 7х₁-4х₂+х₃+3х₄=5 х₁-х₂+х₃-х₄=0

2х₁-3х₂-11х₃-15х₄=1 2х₁+3х₂-5х₃=7 5х₁+7х₂-4х₃-6х₄=3 х₁-х₂+5х₃-х₄=4

х₁+8х₂-7х₃=12 х₁-х₂+6х₃-х₄=5

 

Задача 5. Дана однородная линейная система уравнений. Найти множество решений системы, исследовав ее на совместность через определители.

5.1 х₁-2х₂₊х₃+3х₄=0 5.16 3х₁-2х₂+х₃-4х₄=0

4х₁-х₂+7х₄=0 х₁-8х₂+5х₃-6х₄=0

2х₁+3х₂-2х₃+х₄=0 х₁+3х₂-2х₃-х₄=0

 

5.2 2х₁-3х₂+х₃-2х₄=0 5.17 х₁-3х₂+4х₃-2х₄=0

3х₁-4х₂-2х₃+х₄=0 4х₁-7х₂+10х₃-5х₄=0

х₁-2х₂+4х₃-5х₄=0 2х₁-х₂+2х₃-х₄=0

 

5.3 х₁+2х₂+4х₃-х₄=0 5.18 х₁+2х₂-3х₃+2х₄=0

4х₁+5х₂+11х₃-3х₄=0 х₁-5х₂+7х₃-5х₄=0

2х₁+х₂+3х₃-х₄=0 3х₁-х₂+х₃-х₄=0

 

5.4 3х₁+х₂+2х₃-3х₄=0 5.19 х₁-2х₂+3х₃-2х₄=0

х₁-3х₂-4х₃+х₄=0 4х₁-3х₂+5х₃-х₄=0

х₁+2х₂+3х₃-2х₄=0 2х₁+х₂-х₃+3х₄=0

 

5.5 2х₁-3х₂-2х₃+3х₄=0 5.20 х₁+3х₂-4х₃+2х₄=0

3х₁+2х₂-2х₃-2х₄=0 2х₁-х₂+2х₃-х₄=0

х₁-8х₂-2х₃+8х₄=0 4х₁+5х₂-6х₃+3х₄=0

 

5.6 4х₁-2х₂-3х₃-2х₄=0 5.21 х₁-х₂-х₃+2х₄=0

2х₁-4х₂+х₃+х₄=0 2х₁+3х₂+2х₃-х₄=0

х₁+х₂-2х₃-х₄=0 5х₁-х₃+5х₄=0

 

5.7 3х₁-2х₂+х₃-2х₄=0 5.22 2х₁-3х₂+х₃-2х₄=0

5х₁+2х₂-3х₃-6х₄=0 х₁-8х₂+4х₃-5х₄=0

х₁+2х₂-2х₃-2х₄=0 3х₁+2х₂-2х₃+х₄=0

 

5.8 2х₁-4х₂+х₃+х₄=0 5.23 3х₁-2х₂+х₃-2х₄=0

5х₁-х₂-2х₃-8х₄=0 5х₁+4х₂-3х₃=0

х₁+х₂-х₃-3х₄=0 х₁+3х₂-2х₃+х₄=0

 

 

5.9 3х₁-х₂+х₃-5х₄=0 5.24 2х₁-2х₂+3х₃+х₄=0

х₁-5х₂+5х₃-х₄=0 4х₁+4х₂+х₃+5х₄=0

х₁+2х₂-2х₃-2х₄=0 х₁+3х₂-х₃+2х₄=0

 

5.10 х₁-2х₂+3х₃-4х4=0 5.25 2х₁+х₂-2х₃-х₄₌₀

4х₁-3х₂+5х₃-7х₄=0 4х₁-3х₂+3х₄=0

2х₁+х₂-х₃+х₄=0 х₁-2х₁+х₃+2х₄=0

 

5.11 3х₁-2х₂+х₃-2х₄=0 5.26 х₁-2х₂+3х3+х₄=0

х₁-4х₂+5х₃-6х₄=0 4х₁-3х₂+5х₃=0

х₁+х₂-2х₃+2х₄=0 2х₁+х₂-6х₃-2х₄=0

 

5.12 х₁-3х₂+2х₃-х₄=0 5.27 2х₁-3х₂+х₃-2х₄=0

х₁+7х₂-5х₃+4х₄=0 4х₁-х₂-3х₃-4х₄=0

3х₁+х₂-х₃+2х₄=0 х₁+х₂-2х₃-х₄=0

 

5.13 2х₁-х₂+3х₃+х₄=0 5.28 3х₁+2х₂-х₃-2х₄=0

х₁-4х₂+7х₃=0 х₁+х₂+2х₃+х₄=0

3х₁+2х₂-х₃+2х₄=0 х₁-5х₃-4х₄=0

 

5.14 2х₁-2х₂+х₃-х₄=0 5.29 х₁-2х₂+2х₃-х₄=0

х₁+6х₂-5х₃+4х₄=0 2х₁+7х₂-5х₃+4х₄=0

5х₁+2х₂-3х₃+2х₄=0 4х₁+3х₂-х₃+2х₄=0

 

5.15 х₁-3х₂+2х₃-2х₄=0 5.30 2х₁+4х₂-3х₃+2х₄=0

5х₁-4х₂+3х₃-3х₄=0 4х₁-х₃+4х₄=0

3х₁+2х₂-х₃+х₄=0 х₁-2х₂+х₃+х₄=0

 

 

Задача 6. Решить систему уравнений, исследовав на совместность по теореме Кронекера-Капелли:

6.1 а) 2х₁-х₂+3х₃=0 б) х₁-2х₂+3х₃=0 6.29 а) 2х₁+х₂+3х₃=0 б) 2х₁+х₂+х₃=0

х₁+2х₂-х₃=0 2х₁+х₂-х₃=0 8х₁+3х₂+5х₃=0 3х₁+х₂+3х₃=0

3х₁+х₂+х₃=0 4х₁-3х₂+5х₃=0 2х₁+5х₂-х₃=0 х₁+х₂-х₃=0

 

6.2 а) 2х₁-3х₂+6х₃=0 б) 3х₁-2х₂+х₃=0 6.30 а) 2х₁-5х₂-6х₃=0 б) 3х₁-х₂+4х₃=0

3х₁+4х₂-х₃=0 х₁+х₂-2х₃=0 -3х₁+2х₂+5х₃=0 х₁+х₂+2х₃=0

х₁-5х₂+2х₃=0 х₁-4х₂+5х₃=0 2х₁+4х₂-3х₃=0 х₁-х₂+х₃=0

 

6.3 а) 3х₁+2х₂-х₃=0 б) 2х₁-х₂+3х₃=0

2х₁-х₂+2х₃=0 4х₁+3х₂+х₃=0

5х₁+3х₂-3х₃=0 х₁+2х₂-х₃=0

 

6.4 а) 2х₁-3х₂+4х₃=0 б) 3х₁-х₂+2х₃=0

3х₁+2х₂-х₃=0 х₁-5х₂+8х₃=0

х₁-3х₂+2х₃=0 х₁+2х₂-3х₃=0

 

6.5 а) х₁+2х₂+х₃=0 б) 2х₁+3х₂+4х₃=0

3х₁+2х₂+х₃=0 4х₁-х₂+8х₃=0

х₁+х₂+2х₃=0 х₁-2х₂+2х₃=0

 

6.6 а) х₁+2х₂-х₃=0 б) 3х₁-2х₂+х₃=0

2х₁-3х₂+2х₃=0 х₁+4х₂+5х₃=0

3х₁+х₂+х₃=0 х₁-3х₂-2х₃=0

 

6.7 а) 2х₁+3х₂+2х₃=0 б) 2х₁-3х₂+х₃=0

4х₁+х₂+5х₃=0 4х₁+х₂-3х₃=0

х₁+2х₂+х₃=0 х₁+2х₂-2х₃=0

 

6.8 а) 2х₁+4х₂+х₃=0 б) 5х₁+2х₂+3х₃=0

3х₁+2х₂+2х₃=0 х₁-8х₂+5х₃=0

2х₁+5х₂+х₃=0 2х₁+3х₂-х₃=0

 

 

6.9 а) х₁+2х₂+х₃=0 б) 4х₁-2х₂+х₃=0

3х₁+х₂+2х₃=0 2х₁+2х₂-5х₃=0

5х₁+2х₂+х₃=0 х₁-2х₂+3х₃=0

 

6.10 а) х₁+2х₂+3х₃=0 б) 3х₁-2х₂+4х₃=0

х₁+х₂+х₃=0 5х₁+2х₂+8х₃

х₁+х₂+2х₃=0 х₁+2х₂+2х₃=0

 

6.11 а) 2х₁+х₂-х₃=0 б) 2х₁-3х₂+х₃=0

х₁-2х₂+2х₃=0 4х₁-х₂-3х₃=0

7х₁+х₂-х₃=0 х₁+х₂-2х₃=0

 

6.12 а) 2х₁-3х₂+х₃=0 б) 3х₁+2х₂-х₃=0

5х₁-10х₂+3х₃=0 х₁+4х₂-7х₃=0

4х₁+2х₂+х₃=0 х₁-х₂+3х₃=0

 

6.13 а) 3х₁+2х₂+х₃=0 б) 5х₁-2х₂+3х₃=0

х₁+х₂-х₃=0 3х₁+2х₂-х₃=0

4х₁-х₂+5х₃=0 х₁-2х₂+2х₃=0

 

6.14 а) 2х₁+3х₂-х₃=0 б) 3х₁+2х₂-2х₃=0

х₁+х₂+3х₃=0 х₁+10х₂-2х₃=0

3х₁-4х₂+х₃=0 х₁+3х₂-х₃=0

 

6.15 а) 2х₁+х₂-х₃=0 б) 4х₁+2х₂-х₃=0

3х₁+х₂-2х₃=0 2х₁-4х₂+3х₃=0

х₁+х₃=0 х₁+3х₂-2х₃=0

 

6.16 а) х₁+х₂+х₃=0 б) 3х₁-2х₂+2х₃=0

х₁-х₂+2х₃=0 5х₁-8х₂+4х₃=0

4х₁+х₂+4х₃=0 х₁-3х₂+х₃=0

 

6.17 а) 2х₁-х₂+4х₃=0 б) 4х₁+3х₂+2х₃=0

3х₁-х₂-х₃=0 2х₁+х₂+4х₃=0

-2х₁+х₂+х₃=0 х₁-2х₂-х₃=0

 

 

6.18 а) 3х₁+2х₂-4х₃=0 б) 5х₁+2х₂-3х₃=0

2х₁+4х₂-5х₃=0 2х₁-7х₂-6х₃=0

4х₁-3х₂+2х₃=0 х₁+3х₂+х₃=0

 

6.19 а) 3х₁-3х₂+2х₃=0 б) 3х₁-2х₂+3х₂=0

4х₁-5х₂+2х₃=0 х₁+4х₂+х₃=0

5х₁-6х₂+4х₃=0 х₁-3х₂+х₃=0

 

6.20 а) 5х₁+2х₂+3х₃=0 б) 2х₁-4х₂+5х₃=0

2х₁-2х₂+5х₃=0 х₁-3х₂+3х₃=0

3х₁+4х₂+2х₃=0 3х₁-5х₂+9х₃=0

 

6.21 а) 4х₁-3х₂+2х₃=0 б) 3х₁-2х₂+х₃=0

6х₁-2х₂+3х₃=0 х₁-4х₂+7х₃=0

5х₁-3х₂+2х₃=0 х₁+х₂-3х₃=0

 

6.22 а) 5х₁-6х₂+4х₃=0 б) х₁-4х₂+5х₃=0

3х₁-3х₂+2х₃=0 4х₁-3х₂+4х₃=0

4х₁-5х₂+2х₃=0 2х₁+5х₂-6х₃=0

 

6.23 а) 2х₁+3х₂+5х₃=0 б) 3х₁-6х₂+х₃=0

3х₁+7х₂+4х₃=0 х₁+2х₂+5х₃=0

х₁+2х₂+2х₃=0 2х₁-2х₂+3х₃=0

 

6.24 а) х₁+2х₂+4х₃=0 б) 2х₁-3х₂+х₃=0

5х₁+х₂+2х₃=0 4х₁+х₂-3х₃=0

3х₁-х₂+х₃=0 х₁+2х₂-2х₃=0

 

6.25 а) 3х₁+2х₂+3х₃=0 б) 5х₁-2х₂+3х₃=0

2х₁+3х₂+х₃=0 2х₁+х₂-3х₃=0

2х₁+х₂+3х₃=0 х₁-х₂+2х₃=0

 

6.26 а) 2х₁-х₂-х₃=0 б) х₁-2х₂+3х₃=0

3х₁+4х₂-2х₃=0 2х₁+х₂-х₃=0

3х₁-2х₂+4х₃=0 4х₁-3х₂+5х₃=0

 

6.27 а) 2х₁-х₂+х₃=0 б) х₁+х₂+2х₃=0

4х₁+х₂-2х₃=0 5х₁+3х₂-2х₃=0

х₁-3х₂+х₃=0 3х₁+2х₂-2х₃=0

 

6.28 а) 5х₁-9х₂+4х₃=0 б) 4х₁+3х₂-х₃=0

7х₁-3х₂+5х₃=0 2х₁+х₂+х₃=0

2х₁+4х₂+3х₃=0 х₁+х₂-х₃=0