Теория работы и описание прибора

Приборы и принадлежности

Закрытый стеклянный баллон с краном, манометр, насос

рис. 1

 

Теория работы и описание прибора

Для вещества в любом агрегатном состоянии характерны понятия удельной (с) и молярной (С) теплоемкости. Удельной теплоемкостью вещества называется физическая величина, численно равная количеству теплоты, необходимой для нагревания единицы массы вещества на 1 Кельвин.

(1)

Молярной теплоемкостью вещества называется физическая величина, численно равная количеству теплоты, необходимой для нагревания одного моля вещества на 1 Кельвин.

(2)

Здесь Q – количество теплоты, которое было затрачено на нагре­вание вещества от температуры Т₁ до Т₂. DT = Т₂ — Т₁. Для ве­щества в газообразном состоянии величины удельной или моляр­ной теплоёмкости газа существенно зависят от того, при каких ус­ловиях он нагревается: при постоянном объёме или при постоян­ном давлении.

В первом случае сообщенное газу тепло идёт только на уве­личение внутренней энергии газа, так как объём газа не изменяет­ся и поэтому не совершается работа расширения. Во втором слу­чае требуётся дополнительное количество теплоты, необходимое для совершения работы расширения газа, так как неизменность давления обеспечивается увеличением объёма газа. Поэтому у газа различают две удельные и две молярные теплоёмкости: теплоём­кость при постоянном объёме и теплоемкость при постоянном давлении. Удельной (молярной) теплоемкостью газа при постоян­ном объёме с_v (C_v), или при постоянном давлении с_p (C_p) на­зывается физическая величина, численно равная количеству теп­лоты, необходимой для нагревания единицы массы (моля) на 1 кельвин при постоянном объёме или при постоянном давлении со­ответственно. Между молярной и удельной теплоемкостями оче­видно соотношение:

;

где М — молярная масса газа.

Очевидно, что молярная теплоемкость газа при постоянном давлении больше молярной теплоёмкости при постоянном объёме,

так как , а ,

где R — молярная (универсальная) газовая постоянная, численно равная работе расширения одного моля газа при нагревании его на один кельвин. Тогда .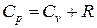

Обозначим отношение теплоёмкостей буквой g, тогда

(3)

Величина g зависит только от числа степеней свободы молекул, из которых состоит газ. Так как , а

где i — число степеней свободы, то

(4)

Численное значение g различно для одно-, двух или многоатом­ных газов и зависит от числа степеней свободы (для одно атомных i = З, двухатомных i = 5 и многоатомных i = 6). На двухатом­ные газы (N₂ и О₂) приходится приблизительно 99% общего соста­ва воздуха, поэтому величину i можно считать приближённо рав­ной 5. Величина отношения теплоёмкостей g имеет большое зна­чение в изучении адиабатных процессов и процессов близких к ним. Например, от этой величины зависит скорость распростране­ния звука в газах, течение газов по трубам со сверхзвуковыми скоростями и другие процессы.

В настоящей работе определяется отношение теплоемкостей g для воздуха (принимая его за двухатомный газ) методом адиа­батного расширения, который основан на применении уравнений адиабатного и изотермического процессов.

Адиабатным процессом называется изменение состояния га­за, при котором не происходит теплообмена с окружающей сре­дой. В этом случае и формула первого закона термодина­мики примет вид , т.е. при адиабат­ном процессе расширения газом совершается работа только расчет изменения запаса внутренней энергии. Этот процесс описы­вается уравнением Пуассона

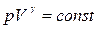(5)

где р — давление и V — объём газа.

Изотермическим называется процесс, который протекает при постоянной температуре, те. Т = const.

В этом случае dT =0, следовательно, dU =0 и тогда из первого закона термодинамики получим . Таким образом, при изотермическом процессе всё подводимое тепло расхо­дуется на работу расширения газа.

Экспериментальная установка состоит из стеклянного баллона А (рис. 11), соёдинённого с манометром В и насосом Н. Через кран К₁ воздух нагнетается в баллон, а через кран К₁ — выпускается. Если кран К₂ открыт, баллон сообщается с атмосферным воз­духом и давление р внутри него равно атмосферному, разность уровней манометра равна нулю, а температура Т в баллоне равна температуре окружающей среды. В процессе работы газ, заключенный в баллоне, проходит последовательно три состояния Если закрыть кран К₂ и накачать в баллон небольшое количество воз­духа, то давление в баллоне будет выше атмосферного, что отме­чается возникновением разности уровней жидкости в манометре. При сжатии воздух в баллоне начнёт нагреваться, затем постепен­но примет температуру окружающей среды, и тогда разность уровней в манометре будет устойчивой, равной р₁. Давление воздуха в баллоне примет величину р+р₁,

где р — атмосферное давление,

р₁ — добавочное давление.

Таким образом, состояние воздуха внутри баллона, которое назовём I состоянием, характеризуется параметрами р + р₁; V₁ и T₁. Если затем открыть кран К₂, то часть воздуха выйдет из бал­лона и давление сравняется с атмосферным, температура газа по­низится до Т₂, а объём будет равен V₂. Этот процесс расширения происходит очень быстро и может считаться адиабатным, так как за короткое время процесса не происходит теплообмена между воздухом в баллоне и окружающей средой. Состояние газа, соответствующее концу адиабатного процесса назовём П состоянием газа с параметрами р; V₂ и Т₂. Адиабатный процесс описывается

уравнением Пуассона .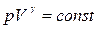

Из уравнения Пуассона следует, что переход газа из I состояния во П может быть выражен в виде:

откуда

(6)

Охладившийся при расширении воздух в баллоне через неко­торое время вследствие теплообмена нагреется до температуры внешней среды T₁, давление возрастёт до некоторой величины р + р₂, где р₂ — новая разность уровней в манометре. Об]ём воз­духа не изменится и будет равен V₂. Это состояние назовём III. Переход газа из II состояния в III происходит в условиях постоян­ного объёма — изохорно. III состояние характеризуется парамет­рами р + р₂; V₂ и T₁. Так как в I и III состояниях воздух имеет одну и ту же температуру (процесс изотермический), то, применяя закон Бойля-Мариотта, будем иметь:

 

откуда получим

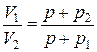(7)

Возведя обе части уравнения в степень g, получим

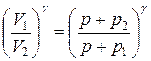(8)

Пользуясь выражением (6) и приравняв правые части (8) и (6), получим

(9)

Прологарифмируем выражение (9) и, решая относительно g, получим:

(10)

Так как практически давление р, р+р₁ и р+р₂ отличаются друг от друга незначительно, то в формуле (10) разности логарифмов можно принять пропорциональными разностям самих давлений и приближенно положить

(11)

Порядок выполнения работы

1. Открыть кран К₁ и при закрытом кране К₂ накачать осторожно с помощью насоса в баллон воздух так, чтобы разность уровней жидкости в манометре составила 25—35 см.

2. Закрыть кран К₁ и, выждав несколько минут, пока уровни жид­кости в манометре перестанут изменятся (это означает, что температура воздуха в баллоне сравняется с температурой ок­ружающей среды) отсчитать по шкале разность уровней р₁ в левой и правой трубках манометра.

3. З. Открыть кран К₂ и, прислушавшись к шипению воздуха, быстро закрыть его по прекращении шипения, что соответствует вы­равниванию давления внутри баллона с атмосферным. Уровень жидкости в манометре будет изменяться, так как исследуемый воздух, охлажденный при адиабатном процессе расширения, нагреется до температуры окружающей среды. Выждав некоторое время, когда разность уровней жидкости в манометре станет ус­тойчивой, отсчитать в миллиметрах эту разность р₂.

4. Открыть оба крана К₁ и К₂ на 2—3 минуты.

5. Пересчитать показания давления р₁ и р₂ из миллиметров во­дяного столба в паскали, принимая, Что 1 миллиметр водяного столба равен 9,81 паскаля.

6. Проделав опыт один раз, вычислить по формуле (11) значение g и сравнить с g, вычисленным теоретически по (4). Если меж­ду ними окажется большое расхождение, то опыт проведён невнимательно с нарушением методики, а поэтому его повторить вновь, добиваясь хорошего совпадения опытного и теоретического значения g.

7. Опыт повторяют 5-7 раз. Результаты измерений заносят в таблицу.­

8. Подставляя в формулу (11) значения р₁ и р₂, взятые из каждого отдельного опыта, вычисляют g₁, g₂, g₃ и т.д. Из найденных значений g найти среднее значение.

 

Таблица наблюдений

№ опыта	p1	p2	g	< g>
Единицы измерения	Па	Па	–	–

 

Контрольные вопросы

1. Какие теплоемкости различают для газов в зависимости от условий нагревания?

2. Что называется удельной, молекулярной теплоемкостью при постоянном объеме, постоянном давлении?

3. Почему С_р больше, чем С_v?

4. Какой процесс называется адиабатным, изотермическим, изохорным?

5. Что происходит с внутренней энергией газа при адиабатном процессе?

6. Как изменяется температура газа при адиабатном процессе?

7. Вывести формулу (11)

8. Выразить С_р и С_v через число степеней свободы молекул газа?

9. Рассчитать теоретически g для различных газов (Н₂, Не, СО₂).