| № варианта | a | b | № варианта | a | b |
| – 289 | – 255 | ||||
| – 112 | – 171 | ||||
| – 175 | – 605 | ||||
| – 735 | – 162 | ||||
| – 625 | – 250 | ||||
| – 108 | – 84 | ||||
| – 375 | – 175 | ||||
| – 147 | – 195 | ||||
| – 255 | – 578 | ||||
| – 338 | – 646 |
Задача №2
Найти (а, b) и [ а, b ], используя канонические разложения чисел а и b. Зна-чения a и b даны в табл. 4 в соответствии с вариантом.
Таблица 4
Исходные данные к задаче №2
| № варианта | a | b | № варианта | a | b |
Задача №3
Решить в целых числах диофантово линейное уравнение ax + by = c. Значе-ния a, b и c даны в табл. 5 в соответствии с вариантом.
Таблица 5
Исходные данные к задаче №3
| № варианта | a | b | c | № варианта | a | b | c |
| – 12 | – 288 | – 252 | |||||
| – 12 | – 171 | – 270 | |||||
| – 75 | – 63 | – 340 | |||||
| – 10 | – 35 | – 162 | |||||
| – 7 | – 62 | – 25 | |||||
| – 108 | – 84 | – 105 | |||||
| – 375 | – 165 | – 132 | |||||
| – 77 | – 147 | – 195 | – 351 | ||||
| – 80 | – 255 | – 575 | |||||
| – 38 | – 46 | – 23 |
Задача №4
Решить в целых числах линейное сравнение ax º b (mod m). Значения a, b и m даны в табл. 6 в соответствии с вариантом.
Таблица 6
Исходные данные к задаче №4
| № варианта | a | b | m | № варианта | a | b | m |
Задача №5
Найти число обратимых классов вычетов в Z / m Z. Значения m указаны в табл. 7 в соответствии с вариантами.
Таблица 7
Исходные данные к задаче №5
| № варианта | m | № варианта | m |
Окончание табл. 7
Задача №6
Заданы три вещественных функции f, g и h. Требуется:
1) найти области определения функций f, g, h и построить композиции функций fgh, hfg, ffg, указав области определения данных композиций;
2) исследовать функции f, g, h на инъективность, сюръективность, биектив-ность на R;
3) найти обратные функции для f, g, h, если они существуют (или найти обратные функции для инъективных сужений функций f, g, h), указав области определения и значений обратных функций.
Формулы f (x), g (x) и h (x) даны в табл. 8 в соответствии с вариантом.
Таблица 8
Исходные данные к задаче №6
| № варианта | f (x) | g (x) | h (x) |
| 3 x + 8 | 3 х | – 4 х 3 + 27 | |
| sin(6 x) | arctg(2 x) – 3 | 5 x – 9 | |
| x 4 + 7 | – 3 x + 2 | 7 x + 15 | |
| 2/(x + 1) | 8 x 7 – 16 | cos(10 x) | |
| 2 x 11 – 3 | x /(x + 3) | – 9sin(12 x) + 3 | |
| – 2 x + 13 | – 3 х 3 + 8 | 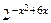
| |
| – 3 x + 4 | 3– x + 17 | х 3 + 12 | |
| – sin(2 x) + 3 | – 16arctg(5 x) + 3 | – 5 x + 19 | |
| – 3 х 4 + 6 | – 5 x + 12 | 7 x + 29 | |
| – 12 x /(x – 1) | – 13arctg(7 x) – 20 | – 5ln(x 2 + 1) | |
| – 6/(x 2 + 3) | 
| 
| |
| – 17 x + 3 | 
| х 2 – 13 x – 5 | |
| 27 x – 18 | – 3 x 7 + 21 | 
| |
| – 3cos(5 x) + 7 | – 3 x 5 + 18 | 
| |
| 3 x + 14 | 3 x – 17 | х 2 – 2 x + 7 | |
| 3 x 13 + 27 | 2arccos(5 x) | log5(2 x + 7) – 10 | |
| sin(3 x) – 2 | 6arctg(5 x) – 3 | 15 x + 9 |
Окончание табл. 8
| х 4 + 16 | 5 x + 2 | 7 x – 19 | |
| 2/(x 2 + 1) | 3arctg(7 x) + 9 | ln(x + 1) | |
| (x – 1)/(x + 2) | 
| 
|
Задача №7
f: V 2(Z / m Z) ® V 2(Z / m Z), где f (c) = A c, A Î M 2(Z / m Z). Обратима ли функ-ция f? В случае положительного ответа найти обратную функцию f – 1. Значения m и матрицы A даны в табл. 9 в соответствии с вариантами.
Таблица 9
Исходные данные к задаче №7
| № варианта | m | A | № варианта | m | A |

| 
| ||||

| 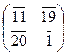
| ||||

| 
| ||||

| 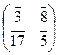
| ||||

| 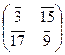
| ||||

| 
| ||||

| 
| ||||

| 
| ||||
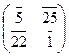
| 
| ||||

| 
|
Задача №8
Доказать, что множества Х и Y равномощны, построив взаимно однозначное соответствие между ними. Множества X и Y даны в табл. 10 в соответствии с вариантом.
Таблица 10
Исходные данные к задаче №8
| № варианта | X | Y | № варианта | X | Y |
| [– 3; 4) | [2; 5]È[7; 9] | 3Z | NÈ{– 1, – 2} | ||
| (– 7; 12] | [3; 6]È{8} | [0; 1] | [0; 1]È[6; 7] | ||
| [– 4; 13] | [– 3; 3]È{4}È{17} | R | (– 2; 4) | ||
| [– 28; 13) | R | (0; 2) | R | ||
| NÈ{0, 1/2} | Z | [– 2; 4] | [2; 4) | ||
| [0; 1) | [0; 1]È[3; 5] | (– 6; 11) | [– 3; 2] | ||
| [– 7; 7] | [0; 1) | [– 2; 1) | [3; 10] | ||
| [– 2; 1] | (– 2; 1) | [– 1; 1] | (– 1; 1)È{2} | ||
| (0; 1) | (0; +¥) | Z | NÈ{– 1} | ||
| (– 2; +¥) | R | 2Z | NÈ{– 1, 0} |






