Выполнил: студент 1 курса 3 группы
Зонов Андрей
Воронеж 2011 г.
Содержание
| Теория множеств. Основные понятия | |
| Способы задания множеств | |
| Операции над множествами | |
| Свойства операций над множествами | |
| Отношения эквивалентности. Фактор-множества | |
| Отображение множеств. Классификация отображений | |
| Сравнение множеств. Мощность множества |
Теория множеств. Основные понятия
Теория множеств является основополагающим определением современной математики. Она была создана Георгом Кантором в 1860-х гг. Он писал: «Множество есть многое, мыслимое как единое целое». Понятие множества принадлежит к числу основных, неопределяемых понятий математики. Оно не сводится к другим, более простым понятиям. Поэтому его нельзя определить, а можно лишь пояснить. Таким образом, множество – объединение в одно целое объектов, хорошо различимых нашей интуицией или нашей мыслью; совокупность некоторых объектов, определенных общим признаком.
Например,
1. Множество жителей г. Воронежа
2. Множество точек плоскости
3. Множество натуральных чисел ℕи др.
Множества обычно обозначаются большими латинскими буквами(A, B, C и т.д.). Объекты, составляющие данное множество, называются его элементами. Элементы множества обозначаются малыми латинскими буквами(a, b, c и т.д.). Если Х – множество, то запись х∈Х означает, что х есть элемент множества Х или что х принадлежит множеству Х, а запись х∉Х, что элемент х не принадлежит множеству Х. Например, пусть ℕ–множество натуральных чисел. Тогда 5  ℕ, а 0,5∉ℕ.
ℕ, а 0,5∉ℕ.
Если множество Y состоит из элементов множества Х, то говорят, что Y является подмножеством множества Х и обозначают Y⊂Х (или Y⊆Х). Например, множество целых чисел ℤ является подмножеством рациональных чисел ℚ.
Если для двух множеств Х и Y одновременно имеют место два включения Х  Y и Y
Y и Y  Х, т.е. Х есть подмножество множества Y и Y есть подмножество множества Х, то множества Х и Y состоят из одних и тех же элементов. Такие множества Х и Y называют равными и пишут: Х=Y.
Х, т.е. Х есть подмножество множества Y и Y есть подмножество множества Х, то множества Х и Y состоят из одних и тех же элементов. Такие множества Х и Y называют равными и пишут: Х=Y.
Часто используется термин пустое множество - Ø - множество, не содержащее ни одного элемента. Оно является подмножеством любого множества.
Для описания множеств могут использоваться следующие способы.
Способы задания множеств
1. Перечисление объектов. Используется только для конечных множеств.
Например, Х={x1, x2, x3… xn}. Запись Y ={1, 4, 7, 5} означает, что множество состоит из четырех чисел 1, 4, 7, 5.
2. Указание характеристического свойства элементов множества.
Для этого задается некоторое свойство Р, позволяющее определить принадлежность элемента множеству. Этот способ является более универсальным.
Х={х: Р(х)}
(множество Х состоит их таких элементов х, для которых выполняется свойство Р (х)).
Пустое множество можно задать, указав его свойства: Ø={х: х≠х}
Построить новые множества можно с помощью уже заданных, используя операции над множествами.
Операции над множествами
1. Объединением(суммой) называется множество, состоящее из всех тех элементов, каждый из которых принадлежит хотя бы одному из множеств А или В.
А∪ В={х: х  А или х
А или х  В}.
В}.

2. Пересечением(произведением) называется множество, состоящее из всех элементов, каждый из которых одновременно принадлежит как множеству А, так и множеству В.
А∩В={х: х  А и х
А и х  В}.
В}.

3. Разностью множеств А и В называется множество, состоящее из всех тех элементов, которые принадлежат множеству А и не принадлежат множеству В.
А\В={х: х  А и х
А и х  В}
В}

4. Если А – подмножество множества В. То множество В\А называют дополнением множества А до множества В и обозначают А’.
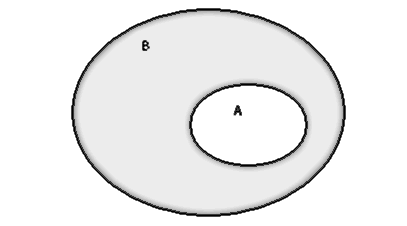
5. Симметрической разностью двух множеств называют множество А∆В=(А\В)  (В\А)
(В\А)

N - множество всех натуральных чисел;
Z - множество всех целых чисел;
Q - множество всех рациональных чисел;
R - множество всех действительных чисел;
C - множество всех комплексных чисел;
Z0 - множество всех неотрицательных целых чисел.
Свойства операций над множествами:
1. А  В=В
В=В  А (коммутативность объединения)
А (коммутативность объединения)
2. А  В=В
В=В  А (коммутативность пересечения)
А (коммутативность пересечения)
3. А(В  С)=(А
С)=(А  В)
В)  С (ассоциативность объединения)
С (ассоциативность объединения)
4. А  (В
(В  С)=(А
С)=(А  В)
В)  С (ассоциативность пересечения)
С (ассоциативность пересечения)
5. А  (В
(В  С)=(А
С)=(А  В)
В)  (А
(А  С) (1 закон дистрибутивности)
С) (1 закон дистрибутивности)
6. А  (В
(В  С)=(А
С)=(А  В)
В) 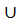 (А
(А  С) (2 закон дистрибутивности)
С) (2 закон дистрибутивности)
7. А  Ø=А
Ø=А
8. А  U= U
U= U
9. А  Ø= Ø
Ø= Ø
10. А  U=А
U=А
11. (А  В)’=А’
В)’=А’  В’ (закон де Моргана)
В’ (закон де Моргана)
12. (А  В)’=А’
В)’=А’  В’ (закон де Моргана)
В’ (закон де Моргана)
13. А  (А
(А  В)=А (закон поглощения)
В)=А (закон поглощения)
14. А  (А
(А  В)=А (закон поглощения)
В)=А (закон поглощения)
Докажем свойство №11. (А  В)’=А’
В)’=А’  В’
В’
По определению равных множеств, нам необходимо доказать два включения 1) (А  В)’ ⊂А’
В)’ ⊂А’  В’;
В’;
2) А’  В’⊂(А
В’⊂(А  В)’.
В)’.
Для доказательства первого включения, рассмотрим произвольный элемент х∈(А  В)’=Х\(А∪В). Это означает, что х∈Х, х∉ А∪В. Отсюда следует, что х∉А и х∉В, поэтому х∈Х\А и х∈Х\В, а значит х∈А’∩В’. Таким образом, (А
В)’=Х\(А∪В). Это означает, что х∈Х, х∉ А∪В. Отсюда следует, что х∉А и х∉В, поэтому х∈Х\А и х∈Х\В, а значит х∈А’∩В’. Таким образом, (А  В)’⊂А’
В)’⊂А’  В’
В’
Обратно, если х∈А’  В’, то х одновременно принадлежит множествам А’, В’, а значит х∉А и х∉В. Из этого следует, что х∉ А
В’, то х одновременно принадлежит множествам А’, В’, а значит х∉А и х∉В. Из этого следует, что х∉ А  В, поэтому х∈(А
В, поэтому х∈(А  В)’. Следовательно, А’
В)’. Следовательно, А’  В’⊂(А
В’⊂(А  В)’.
В)’.
Итак, (А  В)’=А’
В)’=А’  В’
В’
Множество, состоящее из двух элементов, в котором определен порядок следования элементов, называется упорядоченной парой. Для ее записи используют круглые скобки. (х1, х2) – двухэлементное множество, в котором х1 считается первым элементом, а х2 – вторым. Пары (х1, х2) и (х2, х1), где х1≠ х2, считаются различными.
Множество, состоящее из n элементов, в котором определен порядок следования элементов, называется упорядоченным набором из n элементов.
Декартово произведение – произвольное множество X1, X2,…,Xn упорядоченных наборов из n элементов, где x1  X1, x2
X1, x2  X2,…, xn
X2,…, xn  Xn
Xn
Х1 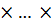 Хn
Хn
Если множества X1, X2,…,Xn совпадают (X1= X2=…=Xn), то их произведение обозначается Хn.
Например, ℝ 2 – множество упорядоченных пар вещественных чисел.
Отношения эквивалентности. Фактор-множества
По данному множеству можно строить новые множества, рассматривая множество некоторых подмножеств. При этом обычно говорят не о множестве подмножеств, а о семействе или классе подмножеств.
В ряде вопросов рассматривают класс таких подмножеств данного множества А, которые не пересекаются и объединение которых совпадает с А. Если данное множество А можно представить в виде объединения своих попарно не пересекающихся подмножеств, то принято говорить, что А разбито на классы. Разбиение на классы осуществляют на основе какого-либо признака.
Пусть Х – не пустое множество, тогда любое подмножество R из произведения Х  Х называется бинарным отношением на множестве Х. Если пара (х,у) входит в R, говорят, что элемент х находится в отношении R с у.
Х называется бинарным отношением на множестве Х. Если пара (х,у) входит в R, говорят, что элемент х находится в отношении R с у.
Например, отношения х=у, х≥у являются бинарным отношениями на множестве ℝ.
Бинарное отношение R на множестве Х называется отношением эквивалентности, если:
1. (х,х)  R;
R; 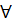 х
х  Х (свойство рефлексивности)
Х (свойство рефлексивности)
2. (х,у)  R => (у,х)
R => (у,х)  R (свойство симметричности)
R (свойство симметричности)
3. (х,у)  R, (у,z)
R, (у,z)  R, то (x,z)
R, то (x,z)  R (свойство транзитивности)
R (свойство транзитивности)
Если пара (х,у) вошла в отношения эквивалентности, то х и у называют эквивалентными (х~у).
1.Пусть ℤ – множество целых чисел, m≥1 – целое число. Зададим отношение эквивалентности R на ℤ так, чтобы n~k, если n-k делится на m. Проверим, выполняются ли свойства на данном отношении.
1. Рефлексивность.
Для любого n∈ℤ  ℤ такого, что (p,p)∈R
ℤ такого, что (p,p)∈R
р-р=0. Так как 0∈ ℤ, то (p,p)∈ℤ.
2. Симметричность.
Из (n,k) ∈R следует, что существует такое р∈ ℤ, что n-k=mp;
k-n =m(-p), -p∈ ℤ, следовательно (k,n) ∈R.
3. Транзитивность.
Из того, что (n,k) ∈R, (k,q) ∈R следует, что существуют такие р1 и р2∈ ℤ, что n-k=mp1 и k-q=mp2. Сложив данные выражения, получаем, что n-q=m(p1+ p2), p1+ p2=p, p∈ ℤ. Поэтому (n,q) ∈ ℤ.
2.Рассмотрим множество Х всех направленных отрезков пространства или плоскости.  =(А, В). Введем отношение эквивалентности R на Х.
=(А, В). Введем отношение эквивалентности R на Х.
 ,
, 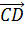 ∈R тогда и только тогда, когда они
∈R тогда и только тогда, когда они
1. Коллинеарны
2. Сонаправленны
3. Равны по длине
Пусть Х – множество, с введенным на нем отношением эквивалентности R. Тогда подмножества А⊂Х называются классом эквивалентности(а̃), если выполняются свойства:
1. А состоит из эквивалентных друг другу элементов.
2. Если х  Х, эквивалентен хотя бы одному а
Х, эквивалентен хотя бы одному а  А, то х
А, то х  А.
А.
Теорема. Два класса эквивалентности либо совпадают, либо не пересекаются и любой элемент из множества Х попадает в один класс эквивалентности.
Доказательство. В теореме считается, что на множестве Х задано отношение эквивалентности R.
А,В⊂Х – 2 класса эквивалентности. Допустим, что А∩В и х∈А∩В.
Докажем, что классы совпадают.
Если а – некоторый элемент из А, то а~х. Так как х∈В, то а∈В. Таким образом, А⊂В. b – некоторый элемент из В, поэтому b~х. Поскольку х∈В, то b∈А. А значит А=В.
Докажем, что А – класс эквивалентности. Любые а,b∈А. По свойству транзитивности а~х, х~b, а следовательно а~b.
Для любого у∈Х у~а, а~х, значит у~х, а значит у∈А. Теорема доказана.
Свойство 2 из определения класса эквивалентности следует из определения класса А.
Пусть Х – множество с отношением эквивалентности R (множество Х состоит из объединения классов эквивалентности).
Совокупность всех классов эквивалентности называется фактор-множеством и обозначается Х/R.
В примере 1 фактор-множеством являются множества целых числе, сравнимых по модулю с m. Это множество состоит из элементов
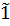 ={1+km, k∈ ℤ};
={1+km, k∈ ℤ};
 ={km, k∈ ℤ}.
={km, k∈ ℤ}.
В примере 2 фактор множество есть множество направлений прямых на плоскости (в пространстве). Каждая из параллельных друг другу прямых (из класса эквивалентности) служит «представителем» направления.






