С6.
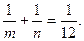
Решение:
Натуральные числа 
разной чётности удовлетворяют уравнению тогда и только тогда, когда
Причём числа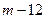 
и 
разной чётности.
В качестве возможного разложения
где p- нечётно, а q -чётно, имеем следующие варианты:
1) 
Поэтому требуемое равенство невозможно.
Ответ: (13;156), (15;60), (21;28).
1. Докажите, что при любом натуральном 
не делиться нацело на 121.
Ответ:
2. Найдёте ли десятизначное число, делящееся на 11,в записи которого использованы цифры от 0 до 9?
Ответ: Например: 9576843210
3. Найдите все решения в целых числах 
.
Ответ: 
4. Найдите решение в натуральных числах 
.
Ответ: 
5. Подряд написаны числа 1, 2, 3, …, 2010. Каких цифр при этих чисел использовано больше – единиц или двоек? На сколько одних цифр больше, чем других?
Ответ: Единиц на 901больше, чем двоек
6. Множество А состоит из натуральных чисел. Количество чисел в А больше семи. Наименьшие общее кратное всех чисел из А равно 210. Для любых двух чисел из А их наибольший общий делитель больше единицы. Произведение всех чисел из А делиться на 1920 и не является квадратом никакого целого числа. Найти числа, из которых состоит А.
Ответ: 6,10,14,30,42,70,105,210
7. При каком наименьшем число 2010! Не делиться на 
?
Ответ: 47
8. Найдите все пары пятизначных чисел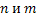 
такие, что число 
полученное приписыванием десятичной записи числа 
после десятичной записи числа , делиться на 
.
Ответ: 16667 и 33334
9. Найдите все натуральные числа, являющимися степенью двойки, такие, что после зачёркивания первой цифры их десятичной записи снова получается десятичная запись числа, являющегося степенью двойки.
Ответ: 32 и 64
10. Найдите все решения в целых числах уравнения 
Ответ: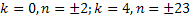 
11. Найдите все пары натуральных чисел, наименьшее общее кратное которых равно 78, а наибольший общий делитель равен 13.
Ответ: 78 и 13 или 26 и 39
12. Найдите все пары натуральных чисел, разность которых 66, а их наименьшее общее кратное равно 360.
Ответ: 90 и 24
13. Найдите все пары натуральных чисел, разность квадратов которых равна 55.
Ответ: 28 и 27 или 8 и 3
14. Найдите все пары таких чисел, для которых их сумма, произведение и разность квадратов одинаковы.
Ответ: 
15. Найдите двузначное число, которое на 19 больше суммы квадратов его десятичных цифр и на 44 больше удвоенного произведения его цифр.
Ответ: 72
16. Произведение натурального числа и числа, записанного теми же цифрами в обратном порядке, ровно 2430. Найдите все такие числа.
Ответ: 54 и 45
17. Найдите все натуральные значения , удовлетворяющие уравнению
где 
– наибольшее целое число, не превосходящее 
.
Ответ: 
18. Натуральные числа 
таковы, что НОК(
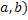= 60, НОК(
= 270 (НОК(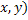
- наименьшее общее кратное чисел 
). Найдите НОК 
Ответ: 108 или 540
19. На клетчатой бумаге отмечен прямоугольник с вершинами в узлах сетки клеток, причем числа m и n взаимно простые и m<n. Диагональ этого прямоугольника не пересекает ровно 116 клеток из этого прямоугольника. Найдите все возможные значения m и n.
Ответ: (2;117) и (3;59)
20. Существуют ли рациональные числа x, y, u, v, которые удовлетворяют уравнению 
?
Ответ: Таких чисел нет
21. Каким может быть наибольший общий делитель натуральных чисел m и n, если при увеличении числа m на 6 он увеличивается в четыре раза?
Ответ: 2 или 6
22. Натуральные числа a, b, c, d, удовлетворяют условию ab= cd. Может ли число a+b+c+d быть простым?
Ответ: не может
23. Найдите все натуральные числа, не представимые в виде суммы двух взаимно простых чисел.
Ответ: 1,2,3,4 и 6
