Математическому выражению, над которым будут производиться преобразования можно присвоить имя. Например, сделав запись
> P:=x^2+2*x+3
P:=x2+2x+3

Рис. 2. Контекстное меню
В дальнейшем, к данному выражению можно обращаться по этому имени.
> P^2
(x2+2x+3)2
По нажатию правой клавиши мыши, можно вызвать контекстное меню (рисунок 2), в котором пользователю предлагаются основные математические операции возможные с данным выражением, такие как дифференцирование (Differentiate), интегрирование (Integrate), разложение на множители (Factor), упрощение (Simplify), решение уравнения в случае равенства нулю (Solve), разложение в ряд по степеням x (Series), двумерные и трехмерные графики (Plots), раскрытие скобок (Expand), приведение подобных членов (Collect) и др.
Функция от одной или нескольких переменных в программе Maple задается следующим образом
>f:=x->x^2+4
f:=x->x^2+4
Эту же структуру, можно выбрать на палитре Expression.
Рассчитаем значения функции при различных значениях аргумента:
> f(2)+f(1)^2-8
25
Интерфейс справочной системы
 Рис. 3. Интерфейс справочной системы
Рис. 3. Интерфейс справочной системы
Maple снабжен мощной диалоговой системой контекстной помощи. Окно справочной системы показано на рисунке 3:
Для получения справки по конкретной команде, следует в контекстном меню выбрать пункт Help on Command.
Анализ ошибок (Error)
В ряде случаев возникают ошибки выполнения вводимых команд. Для установления причины ошибки необходимо перейти по гиперссылке, нажав на сообщение об ошибке (требуется подключение к сети Интернет).
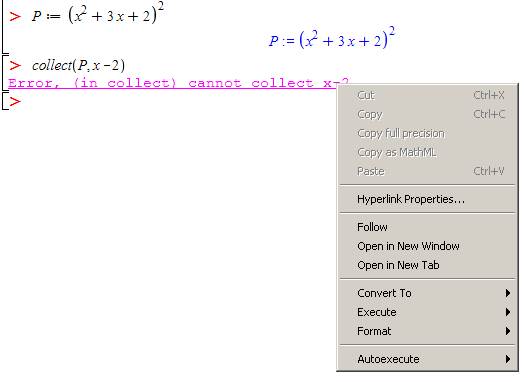
Рис. 4. Переход по гиперссылке из контекстного меню
Построение графиков
Для построения двумерных графиков функций в Maple используется графическая библиотека plots, и встроенная функция plot(выражение, диапазон значений аргумента по горизонтальной оси, диапазон значений аргумента по вертикальной оси, цвет, толщина линий). При этом обязательными параметрами являются выражение и диапазон значений аргумента по горизонтальной оси. Диапазон значений аргумента по горизонтальной оси задается в виде х = хmin..хmax.. Диапазон значений аргумента по вертикальной оси задается в виде у = ymin. .уmax..
Например, пусть требуется построить график функции у = cos(x) на отрезке (-2π, 2π). Для построения указанного графика необходимо ввести
> plot(cos(x), х = -2*Pi..2*Pi);
Результат выполнения функции plot() представлен на рис. 4.

Рис. 4. Построение графика функции cos(x)
Выделив полученный график щелчком левой кнопкой мыши, можно изменить его размер. Если щелкнуть по графику правой кнопкой мыши, то появится контекстное меню для его форматирования. С помощью контекстного меню график можно заключить в рамку, изменить вид координатных осей, изменить толщину, тип или цвет линий, а также добавить заголовок графика и легенду.

Рис.5. Контекстное меню для форматирования графика
Если функция принимает бесконечное значение в какой-либо точке (т.е. имеет точку разрыва второго рода), то в списке аргументов встроенной функции plotQ следует указать дополнительный параметр discont = true. Кроме того, может потребоваться ограничить диапазон отображения графика по вертикальной оси. Например, построим график функции у = tg(x) на отрезке (-π, π ). Для этого в командной строке вводим:
>plot(tan(x), х = -Pi..Pi, discont = true);
Полученный график представлен на рис. 6.

Рис.6. Построение графика функции tg(x)
Для построения графика функции, заданной параметрически, используется следующий формат функции plot():
Plot([func1(t),func2(t), t = a..b], <options>),
где func1(t), func2(t) — функции координат, зависящие от параметра; (а, b) — интервал изменения параметра. Параметр options включает в себя дополнительные опции; например, numpoints — для указания числа точек при построении кривой; coords — для указания типа системы координат; title — для введения заголовка и т.д. При построении графика функции, заданной в полярных координатах, в списке параметров указывается coords = polar.
Например, нам необходимо построить график

Для этого в командной строке вводим:
>plot ([sin(2*t), cos(3*t), t = 0..4*Pi]);
Полученный график представлен на рис. 7.
* 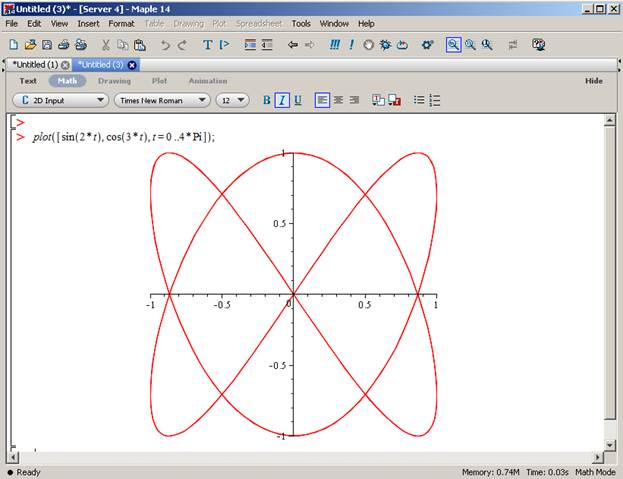
Рис.7. Построение функции, заданной в параметрической форме
Для доступа к другим встроенным функциям пакета plots в командной строке вводим:
> with(plots)
открываем пакет. На экране отобразится перечень графических функций пакета plots (рис.8), для изучения которых можно обратиться к справочной системе Maple 14. Выделив любую функцию списка и нажав <F1>, пользователь попадает на страницу системы Help с описанием этой функции и примерами её применения.

Рис. 8. Перечень функций библиотеки plots.
Например, команды implicitplot, implicitplot3d - разработаны для отображения неявных функций. Их синтаксис схож с синтаксисом команды plot. Для отображения графика функций, заданной в полярной системе координат, в пакете plots существует функция polarplot(). Ее синтаксис похож на синтаксис команды plot() за одним исключением - не задается третий параметр, ограничивающий диапазон изменения значений, в данном случае длины радиус-вектора: polarplot(r, phi=диапазон, опции).
Построение поверхностей происходит аналогично построению кривых на плоскости. Графическая функция, предназначенная для построения поверхностей, имеет следующий формат:
plot3d(f(x, у), х = а..b,у = c..d),
где f{x,y) — функция, график которой требуется построить; диапазоны значений аргументов х и у задаются в виде х = а..b, у = c..d.
Параметрически заданные поверхности строятся с помощью функции plot3d(), имеющей формат:
plot3d([f1 (u, v),f2(u, v),f3(u,v)], u = a..b,v = c..d]).
где f1(u, v),f2(u, v),f3(u, v) — функции координат, зависящие от параметра; а..b, c..d — интервалы изменения параметров.
Пусть требуется построить параболоид, заданный уравнением z = х2 +y2. В командной строке вводим
>plot3d(x^2 + у^2, х = -1..1,у = -1..1);
Полученный график представлен на рис.9.

Рис. 9. Параболоид
Форматирование трехмерного графика осуществляется аналогично форматированию двумерного графика с помощью контекстного меню. Так, для добавления координатных осей щелкаем правой кнопкой мыши по графику и, открыв контекстное меню, переходим на строку Axes, затем в ниспадающем меню выбираем, например, вид координатных осей Normal. Заметим, что после щелчка левой кнопкой мыши по графику указатель мыши меняет свой вид на изогнутую стрелку. Удерживая левую кнопку мыши, можно повернуть трехмерный график так, чтобы получить наилучший угол обзора.
| Дополнительно ко всем известным опциям команды plot() нужно отметить опцию grid=[m,n], определяют сетку из m*n точек, на которой вычерчивается кривая. |
При увеличении количества точек в сетке кривая отбражения становится более гладкой без угловых точек. По умолчанию используется сетка 25*25 точек.




