Задача 1. В вершинах квадрата расположены равные положительные заряды +2·10‑7 Кл (рис. 1). В центре квадрата помещен отрицательный заряд. Вычислить, какой величины должен быть отрицательный заряд, чтобы уравновесить силы взаимного отталкивания зарядов, расположенных по вершинам квадрата.
Решение
Для определения величины q 5 используем закон Кулона. Заряды q 1, q 2, q 3, q 4 одинаковы и расположены симметрично. Поэтому рассуждения проводим для одного из четырех зарядов. Определим условие, при котором один из зарядов, например q 1, находился бы в равновесии с зарядом q 5.
 |
Установим силы отталкивания, которые испытывает заряд q 1 от положительных зарядов q 2, q 3, q 4. По принципу суперпозиции поле каждого заряда q 2, q 3 и q 4 действует на заряд q 1 независимо. Это позволяет составить векторную сумму сил отталкивания (F 12, F 13, F 14). Чтобы установить условия равновесия зарядов q 1 и q 5 необходимо положить, что векторная сумма действующих на них сил равна нулю. С учетом сказанного:
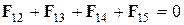, (1)
где F 12, F 13, F 14, F 15 – силы, действующие со стороны зарядов q 2, q 3, q 4 и q 5 на заряд q 1. Учитывая расположение зарядов (см. рис. 1), заменим в выражении (1) F 12 + F 14 на F, после чего получим:
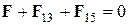. (2)
Переходим от векторного выражения к скалярному:
, 
. (3)
Определяем величину заряда q 5 по закону Кулона:
.
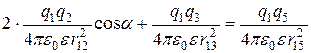Так как q 1 = q 2 = q 3 = q 4 = q, то
. (4)
Кроме того, по условию r 12 = r 14 = r 23 = r 34, тогда
(5)
Подставляя в (4) r 13 и r 15 из (5), после преобразований получаем 
. Производим вычисление в единицах СИ: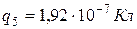 
.
Задача 2. Установить, как изменятся емкость и энергия плоского воздушного конденсатора, если параллельно его обкладкам ввести металлическую пластину толщиной 1 мм. Площадь обкладки конденсатора и пластины 150 см 2, расстояние между обкладками 6 мм. Конденсатор заряжен до 400 В и отключен от батареи.
Решение
Емкость и энергия конденсатора при внесении в него металлической пластины будут изменяться. Это вызвано тем, что металлическая пластина уменьшает расстояние между пластинами с d до (d ‑ d 0) (рис. 2). Используем формулу электроемкости плоского конденсатора:
. (1)
где S ‑ площадь пластины; d ‑ расстояние между пластинами.
Рис. 2
В нашем случае
.
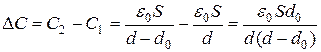Проводим вычисления в единицах СИ
Проверим единицу измерения емкости C
Так как электрическое поле в плоском конденсаторе однородно, плотность энергии во всех его точках одинакова и равна:
, (2)
где E ‑ напряженность поля между обкладками.
При внесении металлической пластины параллельно обкладкам напряженность поля осталась неизменной, а объем электрического поля уменьшился на 
. Следовательно, изменение энергии (конечное значение меньше начального) произошло вследствие уменьшения объема поля конденсатора
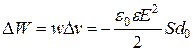. (3)
Напряженность поля E между обкладками плоского конденсатора определяется через разность потенциала на обкладках и расстояние между ними
, (4)
где U ‑ разность потенциалов. Расчетная формула (3) с учетом формулы (4) принимает вид:
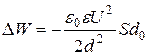, (5)
Подставляя числовые значения (в единицах СИ) в формулу (5), получаем:
Проверяем единицу измерения полученной величины:
.
Задача 3. Катушка без сердечника длиной 
содержит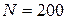 
витков. По катушке течет ток 
. Определить объемную плотность энергии магнитного поля внутри катушки.
Решение
Объемная плотность энергии магнитного поля равна:
, (1)
где 
– энергия магнитного поля катушки, 
– объем катушки, L и S – индуктивность и площадь катушки. Индуктивность катушки дается выражением:
. (2)
Подставив все выражения в формулу (1), найдем объемную плотность энергии магнитного поля внутри катушки:
. (3)
Вычисляя с учетом табличных значений, получаем 
. Проверим единицу измерения полученной величины:
.
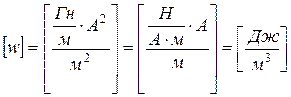Задача 4. Электрон, влетев в однородное магнитное поле с магнитной индукцией 
, движется по окружности радиусом 
. Определить магнитный момент pm эквивалентного кругового тока.
Решение
Так как движение электрона по окружности эквивалентного круговому току, то магнитный момент кругового тока:
, (1)
где e – заряд электрона, 
– период обращения электрона по окружности, 
– площадь, ограниченная окружностью, описываемой электроном.
Электрон совершает движение под действие силы Лоренца Fл. Согласно второму закону Ньютона:
, или 
. (2)
Из выражения (2) получим, что скорость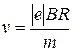 
, а период обращения:
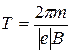. (3)
Подставив выражения для S и T в выражение (1), получим искомый магнитный момент эквивалентного кругового тока:
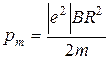. (4)
Вычисляя с учетом табличных значений, получаем 
. Проверим единицу измерения полученной величины:
.
