Цель работы: определить момент инерции маховика с вращающими телами.
Оборудование: маятник Обербека, секундомер.
I. Основные понятия и определения.
Существенное различие между поступательным и вращательным движением заключается в том, что если при поступательном движении все точки тела движутся с одинаковой линейной скоростью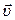 
, направленной по касательной к траектории движения, то при вращательном движении все точки тела движутся с одинаковой угловой скоростью 
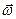, которая направлена вдоль оси вращения, согласно правилу буравчика. Если линейная скорость определяет быстроту изменения координат точек тела с течением времени, то угловая – быстроту изменения угла поворота радиус-вектора точек относительно оси вращения, т.е. 
. Аналогично, угловое ускорение можно определить, как быстроту изменения скорости 
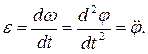
Из особенностей вращательного движения также следует, что оно определяется не только силой 
, но и расстоянием от оси вращения до точки приложения силы. Это обстоятельство учитывается введением понятия момента силы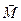 
, который равен произведению силы на её плечо, т.е. 
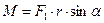, где α – угол между радиус-вектором точки приложения силы и проекцией F1 силы F на плоскость вращения. Вводя характеристики вращательного движения, можно сделать вывод о том, что угловое ускорение пропорционально моменту сил. Коэффициентом пропорциональности должна являться скалярная величина, зависящая не только от массы тела, но и от распределения массы по объёму тела. Она называется моментом инерции 
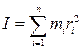, где mi – масса i -го элемента тела, находящегося на расстоянии 
от оси вращения.
Окончательно основное уравнение динамики вращательного движения можно записать в виде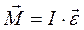 
.
Следует отметить, что момент инерции достаточно просто вычисляется относительно оси, проходящей через центр инерции тела. Если же ось не проходит через центр инерции тела, то весьма полезна теорема Штейнера, согласно которой, момент инерции относительно оси, не проходящей через центр инерции тела Ι, равен моменту инерции относительно параллельной оси, проходящей через центр инерции тела Ι 0, плюс произведение массы на квадрат расстояния d между осями, т.е. Ι= Ι 0+ m d2.
Между величинами, характеризующими поступательное и вращательное движение, существует тесная связь. Например: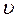 
= ωr, at = εr, где at – тангенциальное ускорение: аналоги между величинами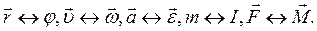 
Поэтому формулы для вращательного движения аналогичны формулам для поступательного движения с соответствующей заменой величины.
II. Методика эксперимента.
Изучение вращательного движения проводится на основе исследования закономерностей вращения маятника Обербека. Маятник сконструирован так, что его момент может меняться путём перемещения тел m по крестовине. Ускорение маятника определяется калиброванным грузом m1, который подвешиваем на нерастяжимую нить.
Уравнение движения ускоряющего груза m1 будет m 1 а =m 1 g-Т1, где Т1 – натяжение нити. С другой стороны, маховик вращается под действием силы натяжения Т2, которая в случае нерастяжимой нити равна Т1, и его уравнение движения: М=Т2·R=Ιε=І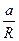 
. Решая совместно систему уравнений поступательного и вращательного движения, для момента инерции маховика получим выражение вида:
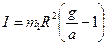. (4.1)
Ускорение движения груза m1 можно определить, измерив пройденный грузом путь h за время t по формуле пути равноускоренного движения: а=2h/ t2. Так что окончательно получим для момента инерции следующее выражение:
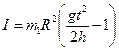. (4.2)
Следует отметить, что при достаточно большом моменте инерции маховика и малом ускоряющем грузе ускорение груза m1 мало. Поэтому отношением 
>>1 и единицей в формуле можно пренебречь. Тогда выражение примет (2.2) вид:
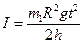. (4.3)
