Метод наименьших квадратов

Вопросы по теме

1. Какое уравнение называется нелинейным?

2. Виды нелинейных уравнений.

3. Что значит решить уравнение?

4. В чём заключается этап отделения корней при использовании численных методов решения уравнения?

5. Какие способы отделения корней вам известны? Сущность этих методов.

6. Метод простой итерации для решения нелинейного уравнения. Графическая интерпретация метода.

7. Какое уравнение можно решать методом итерации?

8. Каковы достаточные условия сходимости итерационного процесса при решении уравнения 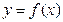на отрезке , содержащего корень, методом простой итерации?

9. Какое условие является критерием достижения заданной точности при решении уравнения 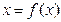методом итерации?

10. Как строится итерационная последовательность точек при решении уравнения методом простой итерации?

11. Метод Ньютона для решения нелинейного уравнения. Графическая интерпретация метода.

12. Условия сходимости метода Ньютона.

13. Модифицированный метод Ньютона.

14. Метод простой итерации для системы из двух нелинейных уравнений.

15. Метод Ньютона для системы из двух нелинейных уравнений.

16. Распространение метода простой итерации на системы уравнений с неизвестными.

17. Распространение метода Ньютона на системы уравнений с неизвестными.

18. Вариационный подход к решению нелинейных систем. Метод наискорейшего спуска.

 

Лабораторная работа № 2

ТЕОРИЯ ИНТЕРПОЛИРОВАНИЯ

 

Задание:

1. Для функции, заданной таблично, построить интерполяционный многочлен Лагранжа и вычислить значение функции в точке .

Вариант		2.0	2.3	2.5	3.0
		5.84	6.13	6.30	6.69	2.02
		11.38	12.80	14.70	17.07	2.09
		3.14	4.15	5.65	6.91	2.91
		6.87	6.41	4.42	3.91	2.85
		7.19	6.21	5.12	3.98	2.44
		1.50	1.34	1.23	1.16	2.13
		1.10	1.05	0.97	0.79	2.25
		1.54	1.61	1.66	1.71	2.32
		0.78	0.39	0.26	0.19	2.79
		0.69	0.35	0.23	0.17	2.94
		1.05	1.21	1.57	2.42	2.48
		6.28	5.62	5.14	4.91	2.59
		1.57	1.21	1.11	1.05	2.64
		1.11	0.74	0.56	0.44	2.71
		1.88	1.54	1.39	1.30	2.12

 

2. Для табличной функции из задания № 1 построить интерполяционный многочлен Ньютона и вычислить значение функции в заданной точке . Сравнить результаты.

3. Для заданной функции построить таблицу значений функции на отрезке 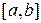, разбив отрезок на равных частей, а затем с помощью интерполирования в форме Ньютона найти значение функции в заданной точке . Определить погрешность интерполирования.

 

Вариант
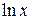
		1.0	1.6		1.55
		-0.2	0.4		-0.11
		0.6	1.2		0.65
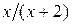
		0.0	0.6		0.54
		0.1	0.4		0.13
		-0.1	0.2		0.18
		0.0	0.3		0.27
		1.2	1.8		1.24
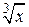
		0.4	1.0		0.45
		0.5	0.8		0.77
		1.1	1.4		1.12
		0.1	0.4		0.37
		0.0	0.3		0.12
		-0.1	0.2		-0.05
		0.4	0.7		0.63

 

4. Для функции, заданной таблицей, найти приближенное значение первой и второй производной в точке

X	0.98	1.00	1.02	1.04
Y	0.7825	0.7739	0.7651	0.7473

, – номер варианта.

5. По заданной таблице значений функции определить значения аргументов , соответствующих заданным значениям

X
Y

1) y=25; 2) y=49; 3) y=100; 4) y=64; 5) y=144; 6) y=196; 7) y=169; 8) y=55; 9) y=105; 10) y=200; 11) y=300; 12) y=180; 13) y=150; 14) y=130; 15) y=200.

6. Для функции, заданной таблицей из задания № 3, построить кубический сплайн и вычислить значение функции в указанной точке .

7. Для заданной функции из задания №3, построить таблицу значений функции на отрезке 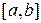, полагая , , , 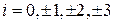. С помощью интерполяционной формулы Гаусса найти значение функции в заданной точке .

Вопросы по теме

1. Что такое интерполяция?

2. Что такое параболическая интерполяция?

3. Что такое узлы интерполяции?

4. В чем заключается задача отыскания интерполирующего многочлена?

5. Теорема о существовании интерполяционного многочлена.

6. Как построить интерполяционный многочлен Лагранжа?

7. Как определяется погрешность метода интерполяции с помощью форму­лы Лагранжа?

8. Какова схема Эйткена?

9. Конечные разности и их свойства.

10. Как образуются разделенные разности (разностные отношения)?

11. Как связаны разделенные разности и производная?

12. Что такое обратное интерполирование?

13. Как строятся многочлены Чебышева?

14. Что такое конечная разность первого порядка? Как она находится?

15. Что такое конечная разность второго порядка? Как она находится?

16. Что такое конечная разность N-го порядка? Как она находится?

17. Первая интерполяционная формула Ньютона для равноотстоящих уз­лов.

18. Вторая интерполяционная формула Ньютона для равноотстоящих уз­лов.

19. Интерполяционные формулы Ньютона для неравноотстоящих узлов.

20. Как находится погрешность метода интерполирования с помощью фор­мул Ньютона?

21. Что значит "интерполирование вперед", "интерполирование назад"?

22. Первая интерполяционная формула Гаусса.

23. Вторая интерполяционная формула Гаусса.

24. Дифференцирование для равноотстоящих узлов.

25. Дифференцирование для неравноотстоящих узлов.

26. Что такое сплайн? Как происходит процесс интерполирования сплайнами?

 

Лабораторная работа № 3

МЕТОД НАИМЕНЬШИХ КВАДРАТОВ

 

Задание:

1. Для заданной функции построить полином второй степени, приближающий с наименьшим квадратичным отклонением на отрезке :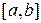

Вариант		a	b
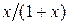
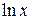
		-1
		-1

2. Для функции , заданной таблично, с помощью метода наименьших квадратов построить аппроксимирующий многочлен второй степени:

Вариант
		-1
		-4
		-1	-2
					-1
		-3		-3
		-2
			-1
				-2	-3
		-3
					-1
		-2	-1

3. Для функции , заданной на отрезке , с помощью метода наименьших квадратов построить обобщенный аппроксимирующий многочлен, взяв в качестве ортогональной системы систему тригонометрических функций 1, , , , :

Вариант		Вариант

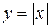
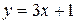
Вопросы по теме

1. Как определяется скалярное произведение двух функций? Норма элемента. Ортогональность.

2. Что называется среднеквадратичным отклонением?

3. Теорема об элементе наилучшего среднеквадратичного приближения.

4. Построение многочлена наилучшего приближения для функции на отрезке.

5. Примеры ортогональных систем многочленов.

 

 

Лабораторная работа № 4

 

ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ИНТЕГРАЛОВ

Задание:

1. Вычислить интегралы по обобщенной формуле трапеций, разбив отрезок интегрирования на частей. Оценить погрешность.

 

Вариант	Подынтегральная функция	a	b	n

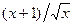
2. Вычислить интеграл по обобщенной формуле Симпсона при заданном числе разбиений отрезка интегрирования, m =4, n =2 m =8. Подынтегральную функцию взять из задания 1. Оценить погрешность.

3. Определить n для обобщенной формулы трапеций при e = 0,001. Подынтегральную функцию взять из задания 1.

4. Вычислить интеграл по формуле Гаусса для . Подынтегральную функцию взять из задания 1.

5. Вычислить интеграл по обобщенной формуле трапеций для и 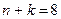узлов и уточнить результат

а) по формуле Ричардсона;

б) по формуле Эйлера n=6;

в) по формуле Ромберга n=8.

6. Вычислить приближенно двойной интеграл

,

где , а функция 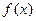и пределы интегрирования и взять из задания 1. Использовать:

а) кубатурную формулу Симпсона с шагами ;

б) метод Гаусса для .

 

Вопросы по теме

1. Определенный интеграл и его геометрическая интерпретация.

2. Квадратурные формулы прямоугольников и их остаточный член.

3. Квадратурная формула Ньютона-Котеса.

4. Квадратурная формула трапеций и ее остаточный член. Геометрическая интерпретация.

5. Квадратурная формула Симпсона и ее остаточный член. Геометрическая интерпретация.

6. Обобщенные квадратурные формулы трапеций и Симпсона и их остаточные члены.

7. Квадратурная формула Гаусса и ее остаточный член.

8. Методы вычисления несобственных интегралов.

9. Уточнение значений интеграла по формуле Ричардсона.

10. Уточнение значений интеграла по формуле Эйлера.

11. Уточнение значений интеграла по формуле Ромберга.

12. Методы вычисления двойных интегралов.

 

 

Лабораторная работа № 5