Лабораторная работа № 2. 3.
Изучение явлений переноса в газах
Определение коэффициента внутреннего трения по формуле Пуазейля
Цель работы: экспериментальная проверка закона Пуазейля. Определение коэффициента вязкости воздуха.
I. Основные понятия и определения
При ламинарном (слоистом) течении газа его движение можно представить как перемещение отдельных слоёв. Между двумя соседними, движущимися друг относительно друга слоями газа, действует сила трения, обусловленная столкновением молекул и передаче импульса направленного движения молекул из слоя в слой. Сила, обусловленная внутренним трением по формуле Ньютона равна:
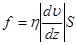, (1)
где постоянная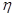 
называется коэффициентом вязкости. Величина 
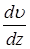показывает изменение скорости среды в направлении оси z, перпендикулярной слоям среды, и называется градиентом скорости; S – площадь соприкосновения слоёв.
Рассмотрим задачу о протекании газа по трубе радиуса r0, между концами которой существует разность давлений Δр = р1 – р2 (см. рис. № 1).
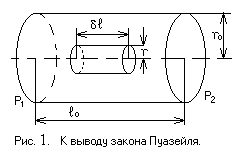Выделим внутри трубы цилиндр радиуса r и длины 
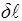. На этот цилиндр в направлении движения действуют две силы. Сила, обусловленная разностью давлений δр на концах цилиндра:
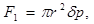(2)
и сила трения на боковую поверхность:
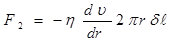. (3)
При записи (3) учтено, что градиент скорости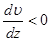 
. Если разность давлений Δр = р1 – р2 мала (Δр << р1, р2), то можно приближённо считать, что плотность газа при движении вдоль трубы не меняется. Тогда в стационарном случае скорость выделенного цилиндра остаётся постоянной. Поэтому равнодействующая сил F1 и F2 равна 0. Так как силы противонаправлены, то находим:
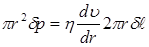. (4)
Суммируя (4) по всем цилиндрам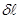 
вдоль оси, отсюда получаем:
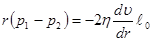(5)
или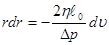 
.
Интегрируя последнее соотношение по dr, с учётом граничного условия υ(r = r0) = 0, находим зависимость υ(r):
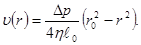(6)
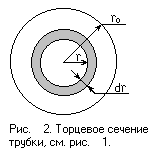
Это выражение описывает распределение скоростей в жидкости по параболическому закону. Для нахождения объёма dV, протекаемого через поперечное сечение трубы за время dt, выделим в этом сечении кольцо радиуса r и толщины dr (см. рис. 2). Объём газа δV, протекаемый через это кольцо за время dt, равен:
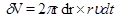, (7)
где υ = υ(r) определяется формулой (6). интегрируя последнее соотношение по dr, с учётом (3.6) получаем:
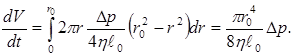(8)
Уравнение (8) называется законом Пуазейля.
II. Методика эксперимента
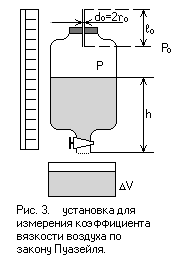
Установка для изучения закона Пуазейля и определения вязкости воздуха (рис. 3) представляет собой бюретку с герметично вставленным сверху капилляром, через который происходит протекание воздуха. Когда кран открывают, давление р воздуха внутри бюретки быстро падает вплоть до того момента, когда объём воздуха, протекающий через капилляр в единицу времени, сравнивается с объёмом воды, вытекающей через кран бюретки в единицу времени (фактически вода идёт по каплям). С установлением стационарного течения начинают измерения. Чтобы применить формулу (8), необходимо знать разность давлений на концах капилляра Δр = р0 – р. Но эта разность как раз уравновешивает воду в бюретке, не давая ей вытекать свободно:
Δp=p0 – p=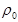 
gh. (9)
За время dt в бюретку натекает объём воздуха:
dV = – S 0 dh, (10)
где S0 – площадь внутреннего сечения бюретки. Подставляя (9) и (10) в закон Пуазейля (8), получаем уравнение для понижения уровня воды:
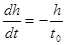, (11)
где
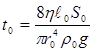(12)
некоторая постоянная времени системы.
Разделяя переменные в (11):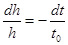 
после интегрирования находим: 
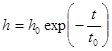или 
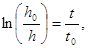(13)
где h0 – начальная высота уровня воды (h(t=0)= h0).
Таким образом, в случае справедливости закона Пуазейля зависимость h(t) имеет экспоненциальный вид.
III. Проведение эксперимента и обработка результатов
1. Наполните бюретку водой. Слив в мерный стакан воду, определите внутреннее сечение бюретки согласно:
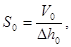
где V0 – объём слитой воды в мерном стакане,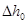 
– понижение уровня воды в бюретке.
2. Вновь заполните бюретку и вставьте пробку с капилляром. Необходимо провести не менее 8 раз измерения величин, входящих в (3.13). Для этого открыть кран и дождаться момента, когда вода станет равномерно капать из крана.
| №п/п |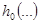 
| 
| 
|
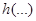
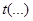
| 1 | |||
| … | |||
| 10 |
Одновременно с запуском секундомера записать высоту h0 уровня воды, а с остановкой – высоту h. Измерения проводите с несколькими значениями времени t. Если необходимо, дополните бюретку водой. Результаты занести в таблицу.
Таблица 1.
3.Отложите на графике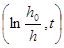 
экспериментальные точки. Отметьте погрешности измерений. Проведите по этим точкам прямую наилучшего приближения. Согласно (13) по наклону этой прямой найдите величину постоянной времени t0 (12).
4. Вычислите вязкость воздуха по (12) и погрешность метода. Составьте и заполните таблицу результатов.
Контрольные вопросы
1. Объясните молекулярно – кинетический механизм вязкости газа.
2. Как вязкость жидкостей и газа зависит от температуры и давления. Каков механизм этой зависимости?
3. Объясните формулу Ньютона для внутреннего трения.
4. Почему скорость слоя газа (жидкости), прилегающего к стенкам трубки, равна нулю?
5. Получите закон Пуазейля в случае трубки с круглым сечением.
6. Пользуясь формулой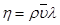 
, где ρ –плотность воздуха, 
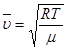– средняя скорость, R – универсальная газовая постоянная, μ – молярная масса, оцените длину свободного пробега λ для воздуха при комнатной температуре. Найдите ρ из уравнения состояния идеального газа.
7. Какова методика эксперимента?
