Лабораторная работа № 5.
Определение момента инерции махового колеса.
Цель работы: изучение законов вращательного движения и определение момента инерции махового колеса.
I. Основные понятия и определения.
Рассмотрим вращение произвольного тела относительно неподвижной оси 
. 
Выделим элементарную массу 
на расстоянии 
от оси вращения. Её уравнение движения 
, где 
- равнодействующая всех сил, действующих на 
-ю точку. Учтём, что вращение этой точки определяется проекцией силы на плоскость вращения 
и нормальной составляющей этой силы 
, т.к. момент силы относительно центра вращения 
. Кроме того 
, где 
- угловое ускорение точки . Следовательно, умножая правую и левую часть уравнения движения на , получим 
. В общем случае равнодействующая определяется как внутренними, так и внешними силами. Просуммируем по всему объёму тела:
.
Т.к. относительно тела точка неподвижна, то момент внутренних сил:
,
тогда момент внешних сил, действующих на тело:
,
где 
- момент инерции тела относительно оси вращения. Таким образом, основной закон динамики вращательного движения тела имеет вид:
. (5.1)
Следует отметить, что в общем случае:
и для симметричных относительно оси вращения тел легко определяется. В таблице 1 приведены моменты инерции симметричных тел:
Таблица 1.
| Тело | 
| Тело |
|
| 
| 
| 
|
| 
| 
| 
|
II. Методика эксперимента.
Установка для изучения законов вращательного движения имеет вид, приведённый на рисунке.
Вращение колеса обеспечивается грузом 
, подвешенного на нити длиной 
. Уравнения движения этой системы грузов: 
, 
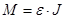или 
, т.е. 
. Тогда из первого уравнения 
, получим
. (5.2)
Так как движение равноускоренное без начальной скорости, то для высоты опускания груза 
имеем 
, где 
- время опускания груза.
В реальной ситуации маховое колесо вращается с трением. Согласно закону сохранения энергии:
, (5.3)
где 
- кинетическая энергия груза, 
- кинетическая энергия маховика, 
- работа сил трения в опоре, 
, где 
- радиус оси маховика по средней линии подшипника.
Когда груз достигнет нижней точки, маховик будет продолжать вращаться, и кинетическая энергия маховика и груза перейдёт в потенциальную энергию груза, когда он поднимется на высоту 
и в работу сил трения 
, т.е.
, 
.
Таким образом,
.
Отсюда:
. (5.4)
Момент инерции определим из измерения времени опускания груза до нижней точки. Однако формула (5.2) не учитывает трения в опоре маховика. Поэтому из формулы (5.3) и (5.4) следует, что
, (5.5)
где 
- диаметр шкива.
III. Проведение эксперимента и обработка результатов.
1) Измерить радиусы шкивов и средней линии подшипника.
2) Выбрать шкив и для него измерить , , для разных масс. Для каждой массы измерения проводить 5 раз. Найти средние 
, 
, 
.
3) Сменить шкив и снова проделать измерения по п.2.
4) По формулам (5.4) и (5.3) вычислить значения силы трения и момента инерции.
5) Результаты измерений и вычислений занести в таблицу 5.2.
Таблица 5.2
| , м
| , м
| , м
|  , Н
| , кгм2
|  , Н
|  , кгм2
|  , кгм2
| 
| |
| ||||||||||
|
Примечание: для более глубокого понимания выполнить электронный вариант работы.
Контрольные вопросы.
1) Как получить основной закон динамики вращательного движения?
2) Как определить момент инерции тела в общем случае и тел, имеющих ось симметрии?
3) Как получить выражение для ускорения груза?
4) Как учесть влияние силы трения и определить её величину?
5) Как определить момент инерции маховика из измерений параметров его движения с учётом трения в опоре?
6) Как оценить достоверность результата измерений?
