Порядок выполнения работы. Основные термодинамические понятия, состояния и определения

Теоретическая часть

Основные термодинамические понятия, состояния и определения.

 

Первое начало термодинамики

Рассмотрим формы превращения энергии для частного случая термодинамической системы (рис.1). Подвижный поршень В может двигаться в цилиндре А с газом Е. Площадь поршня S, перемещение dl. Газ находится под давлением Р, он может нагреваться нагревателем С или охлаждаться холодильником Д.

Вдвигая поршень в цилиндр и совершая работу, мы сжимаем газ, в результате чего температура газа повышается и увеличивается его внутренняя энергия. С другой стороны, температуру газа можно повысить иначе – нагреванием, за счет передачи тепла извне от нагревателя С. Мы видим, что в этой системе возможны две формы передачи энергии от одних тел к другим – в форме работы (макроскопические перемещения тел системы под действием сил) и в форме теплоты (части энергии хаотического движения молекул и излучения). Энергия макроскопического механического перемещения может превращаться в энергию теплового движения молекул и наоборот. При этих превращениях соблюдается всеобщий закон сохранения и превращения энергии. Его формулировка для процессов теплообмена, теплопередачи и перехода тепла в другие формы энергии называется первым началом термодинамики.

Теплота, сообщаемая системе, расходуется на увеличение её внутренней энергии и на совершение ею работы против внешних сил

Q=ΔU+A, (1) где Q - кол-во теплоты, полученное системой;

ΔU - изменение её внутреннеё энергии;

А – работа, совершенная системой против внешних сил.

Для бесконечно малого изменения состояния системы (1) будет иметь вид

dQ=dU+dA, (2)

где dQ, dU, dA – бесконечно малые изменения тепла внутренней энергии и работы против внешних сил соответственно.

Теперь введем некоторые понятия и определения, которые будут использоваться в дальнейшем.

 

 

Полная работа системы

Работа термодинамической системы (рис.1) против внешних сил в общем виде имеет вид

dA=p^.dV, (2)

где dV - бесконечно малое перемещение;

p - давление газа Е.

Полная работа А, совершаемая газом при изменении его объёма от V₁ до V_2, определится интегралом

, (3)

Для интегрирования нужно знать зависимость p от объёма.

 

1.3 Удельная теплоёмкость

Удельной теплоёмкостью вещества С называется величина, равная количеству теплоты, необходимому для нагревания единицы массы вещества (1 кг в системе СИ) на 1К

, (4)

 

1.4 Молярная теплоёмкость

Молярная теплоемкость С_m – величина, равная количеству теплоты, необходимому для нагревания 1 моль вещества на 1К:

(5)

где - число молей нагреваемого вещества;

m – масса вещества;

M – молекулярный вес.

 

1.5

Различают теплоёмкости при постоянном объёме C_v и при постоянном давлении C_р – это теплота, требуемая для нагревания системы на 1К при различных условиях нагревания – при неизменном объеме системы (С_V) или неизменном давлении (C_p). Через число степеней свободы молекулы газа они выражаются формулами (6), (7), (8)

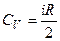, (6)

где i – число степеней свободы у молекул газа;

R - молярная газовая постоянная.

C_p=C_v+R, (7)

Уравнение (7) называется уравнением Майера, оно показывает, что С_p всегда больше C_v на величину молярной газовой постоянной R.

Соотношение (7) обусловлено тем, что при нагревании газа при постоянном давлении требуется дополнительное количество теплоты на совершение работы расширения газа, а R, как будет показано ниже, равна работе расширения 1 моля газа. Постоянство давления обеспечивается увеличением объёма.

Из (6) и (7) следует:

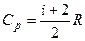, (8)

1.6

При рассмотрении термодинамических процессов важно знать характерное для каждого газа соотношение C_p и C_V

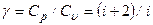, (9)

Эта величина (γ) входит в уравнение Пуассона

pV^γ=const, (10)

являющееся уравнением газового состояния при адиабатических процессах (например, газа в цилиндрах двигателей внутреннего сгорания).

Адиабатический процесс

Адиабатическим называется процесс, при котором отсутствует теплообмен (dQ=0) между термодинамической системой и окружающей средой. Близкими к адиабатическим являются все быстро протекающие процессы. Для нашей модельной системы (рисунок 1) процесс будет адиабатическим, если теплопередачи из объема под поршнем нет или она пренебрежимо мала за время движения поршня.

Теперь рассмотрим результаты применения первого начала термодинамики ( закона сохранения энергии) к изопроцессам, т.е. процессам, в которых один из основных параметров сохраняется постоянным. Фактически это решение системы уравнений первого начала и уравнения газового состояния и исследование свойств этих решений.

 

1.8 Изохорный процесс (V=const)

При изохорном процессе (для системы рисунок 1 – поршень не движется, но теплообмен происходит, меняются давление и температура) объём системы не меняется (dV=0), следовательно газ не совершает работы над внешними телами (рисунок 1, dl =0). Аналитически факт равенства работы нулю можно записать так:

dA=pdV=0, (11)

Из первого начала термодинамики в дифференциальной форме (2) dQ=dU+dA, для изохорного процесса (V=const, dA=0) следует, что,

dQ=dU, (12)

т.е. вся теплота dQ, сообщаемая газу, идет на увеличение его внутренней энергии dU.

Для произвольной массы газа m с молекулярным весом М

, (13)

 

1.9 Изобарный процесс (p=const)

При изобарном процессе расширение газа (рисунок 1, поршень движется при постоянном давлении) работа газа при изменении объёма от V₁ до V₂ равна

, (14)

где P=const, V₂ – конечный объём, V₁ –начальный объём.

Если газ Е близок по свойствам к идеальному, то можно использовать уравнение Клапейрона-Менделеева для описания связи параметров двух выбранных состояний (P=const, V₁,T₁) и (P=const, V₂, T₂): ; , откуда следует и работа изобарного расширения (14) равна

, (15)

Из (15) можно видеть, что физический смысл молярной газовой постоянной R состоит в том, что R численно равно работе расширения одного моля идеального газа при нагревании его на 1К (см. уравнение Майера (7)).

Используя первое начало (2) и выражение для работы газа (15), можно показать, что в изобарном процессе изменение внутренней энергии dU при нагревании на dT равно

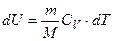, (16)

при этом газ совершает работу (15), а тепла затрачивается

, (17)

 

1.10 Изотермический процесс (T=const)

Переменные p,V,T в изотермическом процессе связаны уравнением Бойля-Мариотта: pV=RT=const. Работа газа в изотермическом процессе (рисунок 1, поршень движется в цилиндре при постоянной температуре; имеет место теплообмен; давление и объём меняются) описывается выражением

.

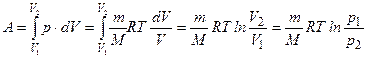Из первого начала термодинамики (2) dQ=dU+dA следует, что для изотермического процесса

dQ=dA, (18)

т.к. при T=const в идеальном газе его внутренняя энергия U не изменяется

, (19)

то всё количество теплоты, сообщаемое газу, расходуется на совершение им работы против внешних сил

, (20)

Это возможно в случае изотермического процесса только тогда, когда постоянно подводится тепло в количестве, эквивалентном внешней работе расширения (т.е. при постоянном нагреве).

1.11 Адиабатический процесс (dQ=0)

Адиабатический процесс (dQ=0) – отсутствует теплообмен между физической системой и окружающей средой. Близки к адиабатическим быстро протекающие процессы.

Из первого начала для адиабатического процесса следует

dA=-dU, (21)

т.е. внешняя работа совершается за счет изменения внутренней энергии системы. Используя уравнение состояния для идеального газа , после ряда преобразований (21), можно получить следующую связь параметров процесса p, V:

, (22)

где .

Это соотношение называется уравнением Пуассона для адиабатического процесса, и оно является уравнением газового состояния. Работа адиабатического расширения для идеального газа определится выражением:

, (23)

где T₁ и T₂ – начальная и конечная температуры.

2. Описание метода измерения γ и используемой аппаратуры.

Поскольку удельная теплоёмкость при постоянном объёме C_V равна (7):

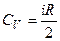
где i – число степеней свободы молекул газа, R - молярная газовая постоянная, а удельная теплоёмкость при постоянном давлении C_p равна (8):

,

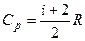то теоретическое значение 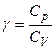равно (9):

.

Для одноатомного газа (He, Ar) число степеней свободы i =3, поэтому . Для двухатомных газов (N₂, O₂) i =5, 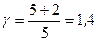. Для многоатомных газов (CH₄) i =6, поэтому . Это теоретические расчетные значения γ. Показатель γ входит в уравнение Пуассона (10) 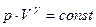, поэтому нам необходимо измерить параметры какого-либо адиабатического процесса для того, чтобы определить γ экспериментально, опытным путем. В настоящей работе определяется γ для воздуха (смесь N₂ и O₂ с малыми примесями иных газов), т.е. воздух в основном двухатомный газ. Для них i =5 и расчетное γ=1,4.

На рисунке 2 изображен измерительный стенд.

Рисунок 2 – Измерительный стенд

В него входят: 1 – баллон, в который электронасосом может нагнетаться воздух, давление которого измеряется манометром 2 со шкалой 3. Кнопкой 6 включается насос, питание насоса включается кнопкой 5. Кран 4 соединяет баллон с атмосферой. Стенд позволяет измерить давление газа в баллоне, которое изменяется в результате прохождения тепловых процессов в объёме газа. Проходящие процессы графически изображены на рисунке 3 в координатах P и V.

В стеклянный баллон 1 (рисунок 2) при помощи насоса 7 накачивают воздух, создавая этим внутри баллона давление выше атмосферного. Это давление измеряется манометром 2. Начальное состояние газа на рис. 3 отображается точкой 1. Давление при этом равно P₁ удельный объём равен V₁, температура t₁ равна температуре воздуха в лаборатории.

 

 

Рисунок 3 -

Быстрое расширение газа можно рассматривать как адиабатическое (без обмена теплом с окружающей средой, теплообмен не успевает произойти). Поэтому, если открыть кран 4 на короткое время, в течение которого давление внутри баллона снизится до атмосферного и снова закрыть его, газ в баллоне адиабатически перейдет в новое состояние 2, характеризуемое давлением P₂, удельным объёмом V₂ и температурой t₂ (точка 2 на рисунке 3). Кривая 1-2, по которой меняются P, V, t- адиабата, описываемая уравнением Пуассона(22)

Температура газа t₂ в конце адиабатического расширения будет меньше, чем t_{1 ,} т.к. совершается работа расширения газа (23) за счет его внутренней энергии (21), что и приводит к снижению температуры. Параметры начального и конечного состояния газа связанны уравнением Пуассона

, (24)

Вследствие теплопроводности стенок баллона газ будет нагреваться до температуры окружающего воздуха t_{1 .} Это происходит за 4-5 минут. Поскольку при этом кран 4 закрыт, V₂ остается неизменным, давление из-за нагрева повысится до P₃ (изохорически, т.к. V=const).

Новое состояние газа характеризуется параметрами (P₃, V₂, t₁) – точка 3 на

рисунке 3. Обратите внимание, температура состояния 3 и 1 – одинаковые, это температура воздуха в лаборатории. Поэтому, в соответствии с законом Бойля-Мариотта, для газа при одной и той же температуре P и V связаны соотношением PV=const, откуда

, (25)

Точка 3 лежит на изотерме 3-1, по которой изменится состояние газа в баллоне до первоначального, исходного 1, если мы откроем кран 4. Эта операция не входит в наши измерения.

Таким образом, мы замерили давление P₁ после накачки, P₂ после кратковременного открытия и закрытия крана и P₃ после нагрева закрытого баллона до температуры окружающего воздуха t₁

Теперь произведем некоторые чисто алгебраические операции с соотношением (25), чтобы избавиться от неизвестных V₁, V₂. Возведем (25) в степень γ и разделим почленно на уравнение (24)

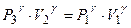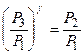; → ; → ; → , (26)

Прологарифмуем уравнение (26)

, (27)

Формула (27) показывает, как по измеренным P₁, P₂, P₃ мы можем рассчитать γ.

Но условия эксперимента позволяют упростить расчетную формулу (27) следующим образом. Обозначим давление в баллоне через P₁, а разность уровней жидкости в манометре через H, тогда

, (28)

где P₂ – атмосферное давление;

b - коэффициент перехода от разности уровней манометра к разности давлений (т.е. цена деления шкалы манометра в единицах давления).

Обозначим через h разность уровней манометра после того, как мы открыли и закрыли кран 4 и выждали 4-5 минут для нагрева газа в баллоне до температуры окружающего воздуха t₁ (т.е. до параметров точки 3 рис. 3). Тогда

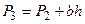, (29)

где P₃ - давление газа в баллоне в точке 3;

P₂ – атмосферное давление;

b – коэффициент перехода от разности уровней к давлению;

h - разность уровней манометра в точке 3.

Из (28) (30) и подставляя его в (29) получим

, (31)

И, наконец, подставляя выражение P₂ из (30) и P₃ из (31) в основную формулу для γ (27), получим

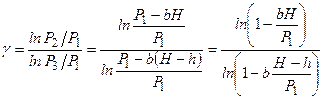, (32)

Величины 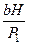и много меньше единицы, поэтому можно воспользоваться формулой 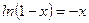, справедливой для малых х с точностью до нескольких процентов. Заменяя логарифмы в (32) на - 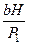и - , получим

, (33)

Формула (33) и будет расчетной в наших измерениях γ.

 

 

Порядок выполнения работы.

1. Включить питание электронасоса выключателем 5.

 

1. Кнопкой 4 включить электронасос и закачать в баллон воздух до разности уровней в манометре от 20 до 30 см.

 

1. Выждать 4-5 минут для выравнивания температуры внутри баллона и температуры окружающего воздуха. Термодинамическая система находится в состоянии, отвечающем точке 1 рисунок 2.

 

1. Измерить разность уровней манометра H, занести результат в таблицу.

 

1. На 1 секунду открыть кран 4 и закрыть его. При этом давление в баллоне адиабатически (без обмена теплом со средой) понизится до атмосферного P₂, а температура внутри баллона станет ниже температуры окружающей среды. Газ в баллоне по адиабате (1-2) (рис.2) перейдет из состояния 1 (P₁, V₁, t₁) в состояние 2 (P₂,V_2, t₂).

 

1. Через 4-5 мин., когда температура в баллоне вновь поднимется до температуры воздуха в лаборатории (t₁), измерить по манометру величину разности уровней манометра h.

 

1. По формуле (33) вычислить величину γ.

1. Результаты измерений и вычислений занести в таблицу. Опыт проделать 5 раз.

 

№п/п	H (см)	h (см)	γi	γср	Δγi	Δγср	Δγср /γср · 100%
. . . .

 

1. Вычислить абсолютную и относительную погрешности измерения γ по следующей схеме:

 

а) по формуле (33) вычислить γ _i для каждого измерения;

 

б) рассчитать среднее значение γ_ср как среднее арифметическое;

 

в) вычислить абсолютную погрешность Δγ_i для каждого измерения:

 

Δγ_i = γ_ср - γ_i

 

г) рассчитать среднюю абсолютную погрешность:

 

Δγ_ср = (1/ т)Σ | Δγ_i |

 

д) окончательный результат записать в виде γ = γ_{ср ±} Δγ_ср

 

е) вычислить относительную погрешность измерений Δγ_{ср /} γ_{ср · 100%}

 

Примечание: атмосферный воздух содержит не только двухатомные газы О₂ и N₂, но и примесь паров воды H₂O и других газов (Аr, Ne, O₃ и др.), поэтому измеренное значение γ всегда отличается от теоретического значения 1,4)

 

 

Контрольные вопросы

1. Опишите используемую установку для измерения γ и изложите ход выполнения работы.

 

1. Какие термодинамические процессы происходят в системе (по графической схеме

рисунка 3)?

 

1. Вывод рабочей формулы .

 

1. Первое начало термодинамики.

 

1. Что такое изопроцессы и их основные свойства для идеального газа.

 

1. Удельные теплоемкости С_p, C_V их связь и вычисления через число степеней свободы молекул.

 

1. Адиабатические процессы и уравнение Пуассона. Когда в данной работе термодинамический процесс имел адиабатический характер?

 

Литература

1. Трофимова Т.И., «Курс физики», гл.9.

2. Сивухин Д.В., «Общий курс физики», т.II., гл. 2, §.21- 22.