Выдержки из дипломной работы Путиловой Т. (руководитнль Клыков И.)
Дифракция света на полуплоскости. Спираль Корню.
Рассмотрим случай, когда часть фронта волны перекрыта экраном в виде полуплоскости. Ограничимся случаем плоской волновой поверхности, что соответствует волне, испускаемой бесконечно удаленным источником.
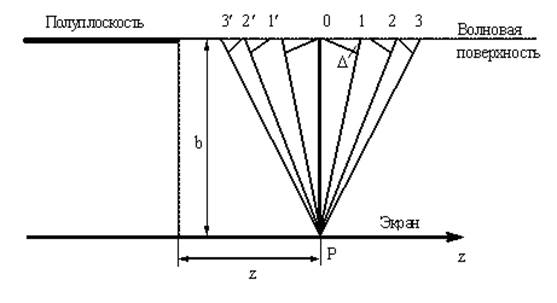 В этом случае для нахождения распределения интенсивности вблизи границы тени, отбрасываемой экраном, принято разбивать волновую поверхность на узкие длинные полоски, параллельные краю полуплоскости, называемые зонами Шустера.
В этом случае для нахождения распределения интенсивности вблизи границы тени, отбрасываемой экраном, принято разбивать волновую поверхность на узкие длинные полоски, параллельные краю полуплоскости, называемые зонами Шустера.
Расположим полуплоскость так, чтобы она совпала с одной из волновых поверхностей. На расстоянии b за полуплоскостью поставим параллельный ей экран, на котором выберем точку P. Разобьем открытую часть волновой поверхности на зоны Шустера. Ширину зон выбираем так, чтобы расстояния от точки P до краев двух соседних зон отличались на одинаковую величину 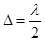 . В этом случае колебания, создаваемые в точке P соседними зонами, будут отличаться по фазе на постоянную величину, равную
. В этом случае колебания, создаваемые в точке P соседними зонами, будут отличаться по фазе на постоянную величину, равную 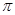 Зоны с номерами m и
Зоны с номерами m и 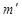 имеют одинаковую ширину и расположены относительно точки P симметрично. Поэтому колебания, создаваемые ими в точке P, совпадают по амплитуде и фазе.
имеют одинаковую ширину и расположены относительно точки P симметрично. Поэтому колебания, создаваемые ими в точке P, совпадают по амплитуде и фазе.
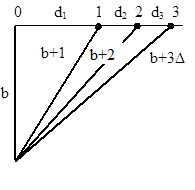 Чтобы установить зависимость амплитуды от номера зоны, нужно оценить площадь зон. Из рисунка видно, что суммарная ширина первых m зон равна
Чтобы установить зависимость амплитуды от номера зоны, нужно оценить площадь зон. Из рисунка видно, что суммарная ширина первых m зон равна 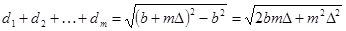
Вследствие узости зон 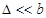 , при небольших m квадратичным членом под корнем можно пренебречь. Тогда
, при небольших m квадратичным членом под корнем можно пренебречь. Тогда 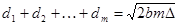 . Так как
. Так как 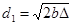 , то суммарная ширина первых m зон может быть представлена следующим образом
, то суммарная ширина первых m зон может быть представлена следующим образом 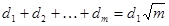 . Тогда ширина зоны с номером m равна
. Тогда ширина зоны с номером m равна 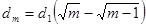 . Из последней формулы можно получить
. Из последней формулы можно получить 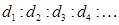 = 1: 0,41: 0,32: 0,27: …
= 1: 0,41: 0,32: 0,27: …
 В таких же соотношениях находятся и площади зон, а, следовательно, и амплитуды колебаний, создаваемых в точке P отдельными зонами. По мере увеличения m скорость убывания амплитуды уменьшается.
В таких же соотношениях находятся и площади зон, а, следовательно, и амплитуды колебаний, создаваемых в точке P отдельными зонами. По мере увеличения m скорость убывания амплитуды уменьшается.
Вычисление интенсивности в точке P удобно проиллюстрировать с помощью векторной диаграммы или методом графического сложения амплитуд. Разобьем волновую поверхность на зоны, аналогичные зонам Шустера. Колебание, создаваемое в точке 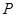 каждой из зон, изобразим в виде вектора, длина которого равна амплитуде колебания, а угол, образуемый вектором с направлением, принятым за начало отсчета, дает начальную фазу колебания. Амплитуда колебаний, создаваемых такими зонами в точке
каждой из зон, изобразим в виде вектора, длина которого равна амплитуде колебания, а угол, образуемый вектором с направлением, принятым за начало отсчета, дает начальную фазу колебания. Амплитуда колебаний, создаваемых такими зонами в точке 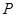 убывает при переходе от зоны к зоне. Так как убывание амплитуды замедляется, то ломаная линия, получающаяся при графическом сложении колебаний, возбуждаемых прямолинейными зонами, идет сначала более полого, чем в случае кольцевых зон. На рисунке представлена векторная диаграмма, соответствующая колебаниям, возбуждаемым зонами, лежащими справа от точки P.
убывает при переходе от зоны к зоне. Так как убывание амплитуды замедляется, то ломаная линия, получающаяся при графическом сложении колебаний, возбуждаемых прямолинейными зонами, идет сначала более полого, чем в случае кольцевых зон. На рисунке представлена векторная диаграмма, соответствующая колебаниям, возбуждаемым зонами, лежащими справа от точки P.
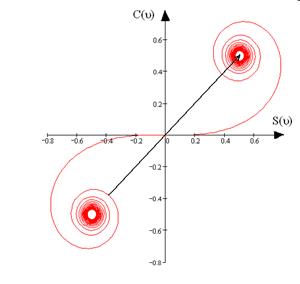
Векторы, изображающие колебания, соответствующие зонам, расположенным слева, при построении диаграммы расположатся симметрично относительно начала координат O. Если ширину зон устремить к нулю, ломаная линия превращается в плавную кривую, которая называется спиралью Корню. Она состоит из двух симметричных ветвей, закручивающихся вокруг фокусов 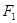 и
и 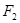 .
.
Уравнение спирали Корню в параметрической форме имеет вид:
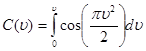
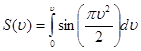
Эти интегралы называются интегралами Френеля. Они не берутся в элементарных функциях, но для них составлены таблицы и графики, по которым можно находить значения интегралов для разных 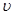 . Смысл параметра
. Смысл параметра 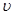 заключается в том, что
заключается в том, что 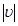 дает длину дуги кривой Корню, измеряемую от начала координат. Точки
дает длину дуги кривой Корню, измеряемую от начала координат. Точки 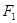 и
и 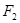 , к которым асимптотически приближается кривая при стремлении
, к которым асимптотически приближается кривая при стремлении 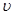 к
к 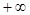 и
и 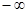 , называют фокусами спирали Корню. Их координаты
, называют фокусами спирали Корню. Их координаты 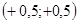 - для точки
- для точки 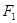 и
и 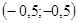 - для точки
- для точки 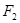 . Отрезок, соединяющий фокусы, имеет длину
. Отрезок, соединяющий фокусы, имеет длину 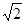 и образует с осью абсцисс угол
и образует с осью абсцисс угол 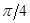 .
.
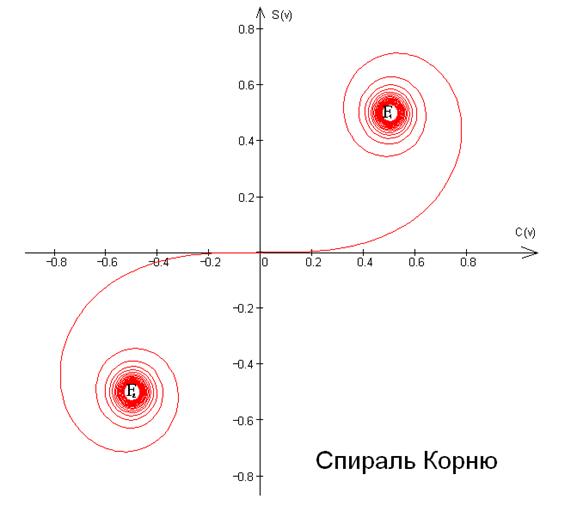
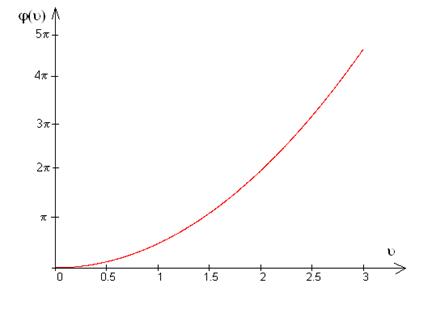
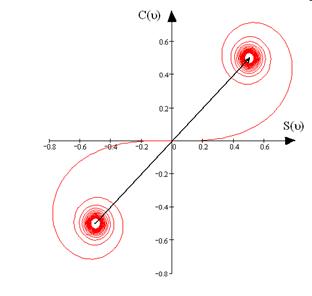
На графике представлена спираль Корню, по координатным осям отложены соответствующие интегралы Френеля.
 |
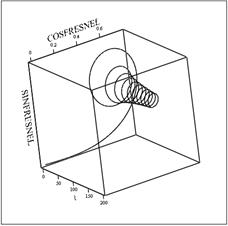
Далее представлена объемная спираль Корню, по осям отложены интегралы Френеля и параметр
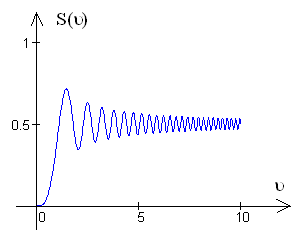
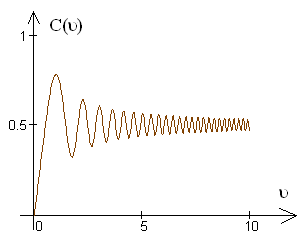
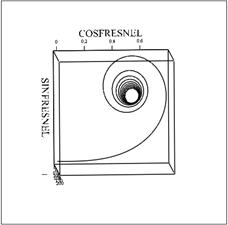
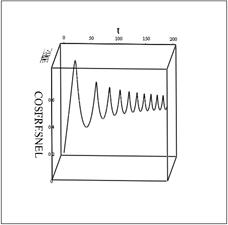
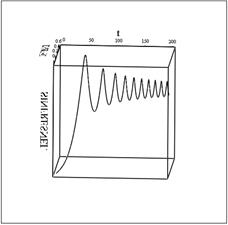
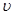 . Так же показано, что проекции объемной спирали Корню на соответствующие координатные плоскости дают, в первом случае, двумерную спираль Корню, в двух других случаях, - графики косинуса и синуса Френеля.
. Так же показано, что проекции объемной спирали Корню на соответствующие координатные плоскости дают, в первом случае, двумерную спираль Корню, в двух других случаях, - графики косинуса и синуса Френеля.
 |
Объемная спираль корню выглядит так:
Найдем производную 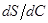 в точке кривой, отвечающей данному значению параметра
в точке кривой, отвечающей данному значению параметра 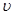 . Приращению
. Приращению 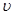 на
на 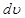 соответствует
соответствует
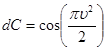
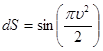
 |
Следовательно,
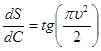 . Вместе с тем
. Вместе с тем 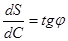 , где
, где 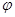 - угол наклона касательной к кривой в данной точке. Таким образом,
- угол наклона касательной к кривой в данной точке. Таким образом,
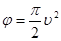
Отсюда следует, что в точке, отвечающей 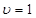 , касательная к кривой Корню перпендикулярна к оси
, касательная к кривой Корню перпендикулярна к оси 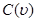 . При
. При 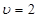 угол
угол 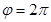 , так что касательная параллельна оси
, так что касательная параллельна оси 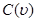 . При
. При 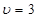 угол
угол 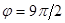 , так что касательная снова перпендикулярна к оси
, так что касательная снова перпендикулярна к оси 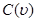 , и т.д.
, и т.д.
Спираль Корню дает возможность найти амплитуду светового колебания в любой точке экрана. Положение точки, в которой определяется интенсивность, будем характеризовать координатой, отсчитываемой от границы геометрической тени. Для точки P, лежащей на границе геометрической тени все штрихованные зоны будут закрыты. Следовательно, результирующее колебание изобразится вектором, начало которого находится в точке O, а конец — в точке 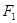 . При смещении точки P в область геометрической тени полуплоскость закрывает все большее число нештрихованных зон. Поэтому начало результирующего вектора перемещается по правому завитку в направлении полюса
. При смещении точки P в область геометрической тени полуплоскость закрывает все большее число нештрихованных зон. Поэтому начало результирующего вектора перемещается по правому завитку в направлении полюса 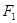 . В результате амплитуда колебаний монотонно стремится к нулю.
. В результате амплитуда колебаний монотонно стремится к нулю.
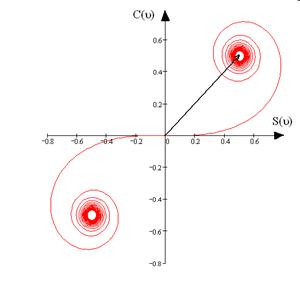
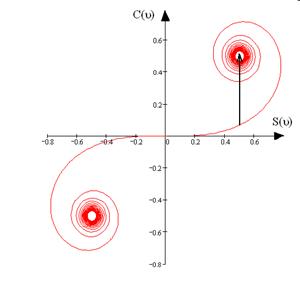
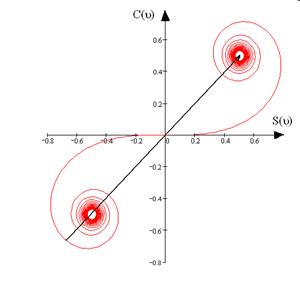
Если точка P смещается вправо от границы геометрической тени, то открываются штрихованные зоны. В этом случае начало результирующего вектора скользит по левому витку спирали в направлении полюса 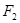 . При этом амплитуда проходит через ряд максимумов и минимумов. При полностью открытой волновой поверхности амплитуда равна длине отрезка
. При этом амплитуда проходит через ряд максимумов и минимумов. При полностью открытой волновой поверхности амплитуда равна длине отрезка 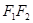 , то есть в два раза превышает амплитуду на границе геометрической тени, а интенсивность на границе геометрической тени в четыре раза меньше интенсивности при полностью открытом волновом фронте.
, то есть в два раза превышает амплитуду на границе геометрической тени, а интенсивность на границе геометрической тени в четыре раза меньше интенсивности при полностью открытом волновом фронте.
 Зависимость интенсивности света
Зависимость интенсивности света 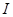 от координаты
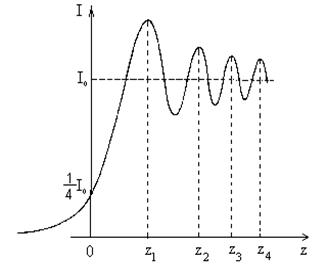
от координаты 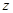 показана на рисунке. Из рисунка видно, что при переходе в область геометрической тени интенсивность меняется не скачком, а постепенно стремится к нулю. Справа от границы геометрической тени располагаются чередующиеся максимумы и минимумы интенсивности. Вычисления дают, что при
показана на рисунке. Из рисунка видно, что при переходе в область геометрической тени интенсивность меняется не скачком, а постепенно стремится к нулю. Справа от границы геометрической тени располагаются чередующиеся максимумы и минимумы интенсивности. Вычисления дают, что при 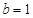 м и
м и 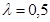 мкм координаты максимумов имеют следующие значения:
мкм координаты максимумов имеют следующие значения: 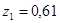 мм,
мм, 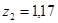 мм,
мм, 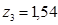 мм,
мм, 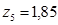 мм и т. д. С изменением расстояния
мм и т. д. С изменением расстояния 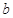 от полуплоскости до экрана значения координат максимумов и минимумов изменяются как
от полуплоскости до экрана значения координат максимумов и минимумов изменяются как 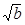 .
.
Дифракция от щели.
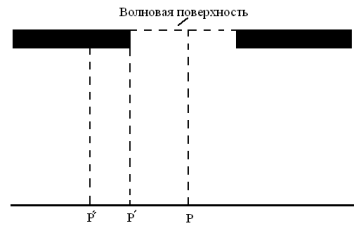
Бесконечно длинную щель можно образовать, расположив рядом две обращенные в разные стороны полуплоскости. Следовательно, Задача о дифракции Френеля от щели может быть решена с помощью спирали Корню. Волновую поверхность падающего света, плоскость щели и экран, на котором наблюдается дифракционная картина, будем считать параллельными друг другу.
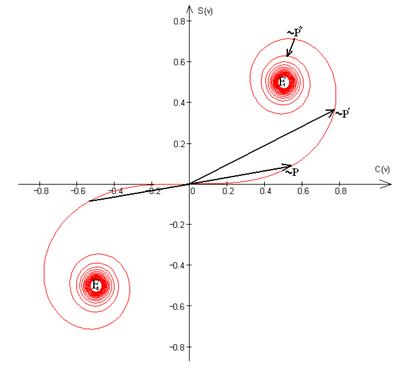
Для точки 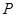 , лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали. Если сместиться в точку
, лежащей против середины щели, начало и конец результирующего вектора находятся в симметричных относительно начала координат точках спирали. Если сместиться в точку 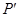 , лежащую против края щели, начало результирующего вектора переместится в середину спирали
, лежащую против края щели, начало результирующего вектора переместится в середину спирали 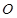 . Конец вектора переместится по спирали в направлении полюса
. Конец вектора переместится по спирали в направлении полюса 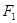 . При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга (см. на рисунке вектор, соответствующий точке
. При углублении в область геометрической тени начало и конец результирующего вектора будут скользить по спирали и в конце концов окажутся на наименьшем расстоянии друг от друга (см. на рисунке вектор, соответствующий точке 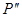 ). Интенсивность света достигнет при этом минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки
). Интенсивность света достигнет при этом минимума. При дальнейшем скольжении по спирали начало и конец вектора снова отойдут друг от друга и интенсивность будет расти. То же самое будет происходить при смещении из точки 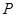 в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.
в противоположную сторону, так как дифракционная картина симметрична относительно середины щели.
 |
Если изменять ширину щели, сдвигая полуплоскости в противоположные стороны, интенсивность в средней точке
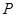 будет пульсировать, проходя попеременно через максимумы и отличные от нуля минимумы.
будет пульсировать, проходя попеременно через максимумы и отличные от нуля минимумы.
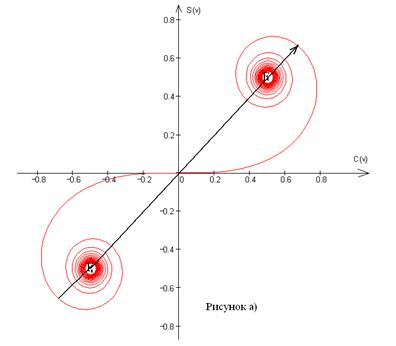 |
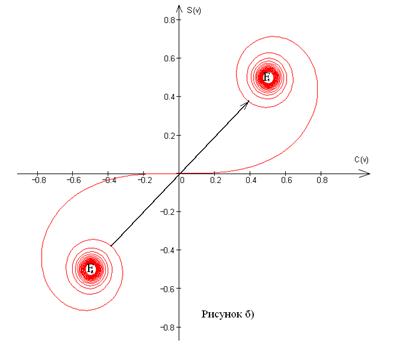
Итак, френелевская дифракционная картина от щели представляет собой либо светлую (рисунок а), либо темную центральную полосу (рисунок б), по обе стороны которой располагаются симметричные относительно нее чередующиеся темные и светлые полосы.
При большой ширине щели начало и конец результирующего вектора для точки 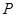 лежат на внутренних витках спирали вблизи полюсов
лежат на внутренних витках спирали вблизи полюсов 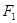 и
и 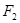 . Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных светлых и темных полос.
. Поэтому интенсивность света в точках, расположенных против щели, будет практически постоянной. Только на границах геометрической тени образуется система густо расположенных светлых и темных полос.






