Интегральное исчисление функций многих переменных

 

В Maple имеются две специальные команды для вычисления двойных и тройных интегралов, содержащиеся в библиотеке student.

Для вычисления двойных интегралов 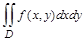используется команда Doubleint(f(x, y), D), где D – область интегрирования, записываемая в одном из следующих форматов:

§ x=х1..х2, y=y1..y2, где числа х1, х2, y1, y2 задают прямоугольную область интегрирования;

§ x=f1(y)..f2(y), y=y1..y2, где f1(y), f2(y) - линии, ограничивающие область интегрирования слева и справа на интервале от y1 до y2;

§ x=х1..х2, y=g1(x)..g2(x), где g1(y), g2(y) - линии, ограничивающие область интегрирования снизу и сверху на интервале от х1 до х2.

Для вычисления тройных интегралов 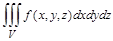используется команда Tripleint(f(x, y, z),x, y, z, V), где V – область интегрирования.

Обе эти команды являются командами отложенного действия. Чтобы получить значение интеграла, следует использовать команду value(%).

Повторные интегралы можно вычислять с помощью повторения команды int, например, повторный интеграл вычисляется командой

> Int(Int(y^3/(x^2+y^2),x=0..y),y=2..4)=int(int(y^3/(x^2+y^2), x=0..y),y=2..4);

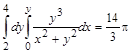
Вычислить двойной интеграл по области, ограниченной линиями .

С начала следует описать область интегрирования D в виде неравенств:

> restart: with(student):

> J:=Doubleint(sin(x+2*y), x=y..Pi/2-y, y=0..Pi/2);

> J:=value(%);

Вычислить тройной интеграл .

> J:=Tripleint(4+z, z=0..2, y=x^2..1,x=-1..1);

> J:=value(%);

Действия с матрицами

Основная часть команд для решения задач линейной алгебры содержится в библиотеке linalg. Поэтому перед решением задач с матрицами и векторами следует загрузить эту библиотеку командой with(linalg).

Для определения матрицы в Maple можно использовать команду matrix(n, m, [a11,a12,…,a1n, a21,a22,…,a2m,…, an1,an2,…,anm]]), где n -число строк, m – число столбцов в матрице. n, mзадавать необязательно, а достаточно перечислить элементы матрицы построчно в квадратных скобках через запятую. Например:

> A:=matrix(2,3,[1,2,3,-3,-2,-1]);

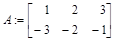
Сложение двух матриц одинаковой размерности осуществляется теми же командами, что и сложение векторов:

1) evalm(A+B)

2) matadd(A,B).

Произведение двух матриц может быть найдено с помощью двух команд:

1) evalm(A&*B);

2) multiply(A,B).

Пример.

> A:=matrix([[1,0],[0,-1]]);

> B:=matrix([[-5,1], [7,4]]);

>v:=vector([2,4]);

>multiply(A,v);

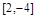
>multiply(A,B);

>matadd(A,B);

Команда evalm позволяет также прибавлять к матрице число и умножать матрицу на число. Например:

> С:=matrix([[1,1],[2,3]]):

>evalm(2+3*С);

 

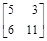
Определитель матрицы А вычисляется командой det(A). Команда minor(A,i,j) возвращает матрицу, полученную из исходной матрицы А вычеркиванием i -ой строки и j -ого столбца. Минор M_ij элемента a_ij матрицы А можно вычислить командой det(minor(A,i,j)). Ранг матрицы А вычисляется командой rank(A). След матрицы А, равный сумме ее диагональных элементов, вычисляется командой trace(A).

>K:=matrix([[4,0,5],[0,1,-6],[3,0,4]]);

>det(K);

>minor(K,3,2);

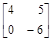
>det(%);

-24

>trace(K);

 

Обратную матрицу А ^-1, такую что А ^-1 А = АА ^-1= Е, где Е - единичная матрица, можно вычислить двумя способами:

1) evalm(1/A);

2) inverse(A).

Транспонирование матрицы А – это изменение местами строк и столбцов. Полученная в результате этого матрица называется транспонированной и обозначается А'. Транспонированную матрицу А' можно вычислить командой transpose(A).

Например, используя заданную в предыдущем пункте матрицу K, найдем ей обратную и транспонированную:

>inverse(K);

>multiply(K,%);

>transpose(K);

В пакете linalgимеются функции решения систем линейных уравнений, отличные от функции solve() из стандартной библиотеки. Для решения системы линейных алгебраических уравнений вида MX=B, где M – матрица, Xвектор из правых частей уравнения, имеются функции linsolve(M,B).

Пусть требуется решить следующую систему уравнений

Запишем систему в матричном виде

Затем в команднойстроке вводим

>with(linalg)

>A:=matrix(2,1,[9,12])

 

>B:=matrix(2,2,[5,2,2,5])

 

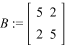
Решаем систему уравнений BX=A:

>linsolve(B,A)

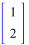
Ответ: x=1, y=2.

Из курса линейной алгебры известно, что если А х =l х, то вектор х называется собственным вектором матрицы А, а число l – собственным числом, соответствующим данному собственному вектору. Совокупность всех собственных чисел матрицы называется спектром матрицы. Если в спектре матрицы одно и тоже собственное число встречается k раз, то говорят, что кратность этого собственного числа равна k.

Для нахождения собственных чисел матрицы А используется команда eigenvalues(A). Для нахождения собственных векторов матрицы А используется команда eigenvectors(A). В результате выполнения этой команды будут получены собственные числа, их кратность и соответствующие собственные векторы.

Чтобы понять, в каком виде получаются результаты выполнения команды eigenvectors, внимательно разберитесь со следующим примером: матрица 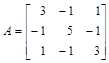имеет 3 собственных вектора: 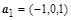, отвечающий собственному числу кратности 1, , отвечающий собственному числу кратности 1, , отвечающий собственному числу кратности 1. Найдем их в Maple:

> A:=matrix([[3,-1,1],[-1,5,-1],[1,-1,3]]):

> eigenvectors(A);

[2,1,{[-1,0,1]}], [3,1,{[1,1,1]}], [6,1,{[1,-2,1]}]

В строке вывода перечислены в квадратных скобках собственное число, его кратность и соответствующий собственный вектор в фигурных скобках, затем следующие наборы таких же данных.

 

Для вычисления характеристического многочлена 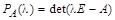матрицы A используется команда charpoly(A,lambda).

 

К треугольному виду матрицу А можно привести тремя способами:

1) команда gausselim(A) приводит матрицу А к треугольному виду методом Гаусса;

2) команда ffgausselim(A) приводит матрицу А к треугольному виду методом Гаусса без деления. Эта команда предпочтительней для работы с символьными матрицами, так как не производит нормировку элементов и исключает возможные ошибки, связанные с делением на нуль;

3) команда gaussjord(A) приводит матрицу А к треугольному виду методом Гаусса-Жордана.

Характеристическую матрицу можно вычислить командой charmat(A,lambda).

Дана матрица . Найти ее собственные векторы и собственные числа.

> U:=matrix([[3,2-I],[2+I,7]]):

> eigenvectors(U);

,

Дана матрица 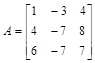. Привести матрицу А треугольному виду, найти ее характеристическую матрицу.

> A:=matrix([[1,-3,4],[4,-7,8],[6,-7,7]]):

>g:=gausselim(A);

>g:=ffgausselim(A);

>F:=charmat(A,lambda);

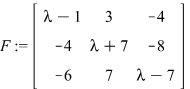
Комплексные числа

 

Комплексное число x+iyвводится в командную строку в виде x+I*y, например

>2+6*I

Действительная и мнимая части комплексного числа находятся встроенными функциями Re(), Im(). Например,

>Re(2+6*I)

>Im(2+6*I)

Для определения сопряженного числа применяется функция conjugate(). Например

>conjugate(2+6*I)

Модуль и главное значение аргумента комплексного числа вычисляются встроенными функциями abs() и argument(). Например

>abs(2+6*I)

>argument(2+6*I)

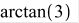
Модуль и главное значение аргумента комплексного числа можно также вычислить с помощью функции polar():

>polar(2+6*I)

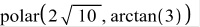
Умножение, деление, возведение в степень комплексных чисел выполняется как и над обычными числами.

Значения функций, у которых аргумент является комплексным числом, находятся с помощью встроенной функции evalc(). Например

>evalc(cos(2+6I))

>evalc(exp(2+6I))

Функция evalc возвращает только главное значение . Например

>evalc((-1)^(1/4))