Применение этого метода для минимизации выражений ФАЛ в классическом базисе было рассмотрено в главе 1. Покажем теперь, что его можно применить для этой же цели и в базисе Вебба, если только учитывать особенности этого базиса. Как и в классическом базисе, запишем функцию с неопределенными коэффициентами для случая трех переменных:
Получаем систему из 23 уравнений для определения неизвестных коэффициентов. При нахождении их следует помнить, что обращение в единицу некоторого выражения, стоящего при неизвестном коэффициенте, требует обращения в нуль всех аргументов этого выражения.
Пример 2-2. Найти минимальную нормальную форму для функции из примера (2-1).
Переходя к системе уравнений с неопределенными коэффициентами для данной функции, получаем:
С учетом того, что все коэффициенты для уравнений, у которых в левой части стоит единица, равны нулю, преобразуем исходную систему к следующему виду:
Как следует из этой системы, 
. Наиболее экономное решение для двух оставшихся уравнений 
, 
.
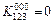Окончательно
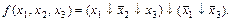
МЕТОД КВАЙНА.
Метод Квайна для минимизации ФАЛ в классическом базисе был рассмотрен в главе 1. Все сказанное там о принципах метода и последовательности выполнения этапов минимизации остается в силе. Только здесь неотмеченные минитермы будут простыми инверсантами функции, и необходимо учитывать возможное вырождение минитермов, сопровождающееся инвертированием оставшейся переменной.
Пример 2-3. Найти минимальную нормальную форму для следующей совершенной нормальной формы функции:
Минитермы третьего ранга
Используем соотношение (2-10) и производим все возможные неполные склеивания между этими минитермами. Минитермы, которые учавствовали хотя бы в одном склеивании, отмечаем звездочкой, так как они в дальнейшем будут поглощены минитермом второго ранга, являющимся результатом склеивания на основании соотношения (2-11). Получим минитермы второго ранга
.
В результате склеивания между первым и последним минитермом получиться вырожденный минитерм, который инвертируется. Тот же самый результат получится из склеивания третьего и четвертого минитермов. Не будет поглощаться только второй минитерм.
Минитерм первого ранга
Удаляя из нормальной формы все поглощающиеся инверсанты, получаем сокращенную нормальную форму, содержащую только простые инверсанты:
Для данного примера сокращенная нормальная форма совпадает с минимальной и построение таблицы меток, и поиск минимального покрытия не дает ничего нового. Отметим, что построение таблицы и операции с нею полностью аналогичны работе с таблицей Квайна. Единственная разница состоит в том, что вырожденная инверсанта, состоящая из единственной переменной, поглощает те минитермы, которые содержат ее отрицание. Для нашего примера для строки, соответствующей инверсанте , мы должны расставить метки в столбцах, которые содержат в соответствующем им выражении 
.
МЕТОД МАК-КЛАСКИ
Усовершенствование первого этапа метода Квайна, предложенное Мак-Класки, применимо и в базисе Вебба. Напомним,что в методе Мак-Класки применяются двоичные номера минитермов. Если принять номер минитерма совпадающим с двоичным номером набора значений переменных, на котором минитерм, являющийся характеристической функцией единицы, принимает значение единицы, или минитерм, являющийся характеристической функцией нуля, принимает значение нуля, то, очевидно, применение метода Мак-Класки не зависит от базиса.
Пример 2-4. Найти минимальную нормальную форму функции,
принимающей значение нуль на наборах с номерами 0, 2, 4, 6, 8, 10, 12, 13, 14.
Воспользуемся случаем показать одну возможность табличного расположения минитермов, преимущество которого состоит в большей наглядности. В этой таблице минитермы одного ранга образуют столбец, а различные группы выделены горизонтальными линиями.
Составление таблицы начинается с первого столбца для минитермов четвертого ранга, которые соответствуют нулям функции. Слева показаны номера групп только для этого столбца.
По неотмеченным наборам строится сокращенная нормальная форма, учитывая что нулю в наборе соответствует xi, а единице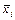 
:
.
Как и в предыдущем примере, единственная переменная вырожденного минитерма 
инвертируется.
| группа | Ранг | |||
| 0000* | 00-0* | 0- -0* | ---0 | |
| 0010* | 0-00* | -0-0* | ||
| 0100* | -000* | --00* |
| |
| 1000* | 0-10* | --10* | ||
| 0110* | -010* | -1-0* | ||
| 1010* | 01-0* | 1- -0* | ||
| 1100* | -100* | |||
| 1101* | 10-0* | |||
| 1110* | 1-00* | |||
| -110* | ||||
| 1-10* | ||||
| 110- | 
| |||
| 11-0* |
В данном случае сокращенная нормальная форма совпадает с минимальной. Если бы этого не было, то пришлось бы строить таблицу инверсант и производить расстановку меток обычным способом.
Отметим, что минимальная ДНФ этой же функции более сложна:
Рассмотрим теперь второй из подходов к минимизации, о котором мы говорили выше. Напомним, что в этом случае минимизация проводится в классическом базисе, а затем полученное минимальное выражение переводится в монофункциональный базис таким образом, чтобы по возможности сохранялась минимальность. Е.И. Пупыревым [15] было показано, что существует такой метод перехода от минимальной ДНФ к ее представлению в монофункциональном базисе, при котором сложность вновь получаемого представления либо минимальна в данном монофункциональном базисе, либо отличается от этой сложности на одну букву. Этот результат говорит еще раз о тесной связи этих базисов между собой.
СПИСОК ЛИТЕРАТУРЫ
1. Акимов О.Е. Дискретная математика: логика, группы, графы. –М.: Лаборатория Базовых Знаний, 2003. -376с.
2. Белоусов А.И., Ткачев С.Б. Дискретная математика. –М.: Изд-во МГТУ им. Баумана, 2004. -744с.
3. Вавилов Е.Н, Портной Г.П. Синтез схем электронных цифровых машин. М.: Изд-во “Советское радио”, 1963. -440с.
4. Гаврилов Г.П., Сапоженко А.А. Сборник задач по дискретной математике. –М.: Наука, 1977. -368с.
5. Глушков В.М. Синтез цифровых автоматов. –М., Физматгиз, 1962г., -476с.
6. Гиндикин С.Г. Алгебра логики в задачах. –М.: Наука, 1972. -288с.
7. Горбатов В.А., Горбатов А.В., Горбатова М.В. Дискретная математика: Учебник для студентов втузов. –М.: ООО”Изд-во АСТ”: ООО”Изд-во Астрель”, 2003. -447с.
8. Журавлев Ю.И. Алгоритмы построения минимальных дизъюнктивных нормальных форм для функций алгебры логики. Дискретная математика и математические вопросы кибернетики. т.1-М: Наука, 1974. –с. 67-98.
9. Лавров И.А., Максимова Л.Л. Задачи по теории множеств, математической логике и теории алгоритмов. –М.: Наука, 1984. -240с.
10. Нефедов В.Н., Осипова В.А. Курс дискретной математики: Учеб. пособие. –М: Изд-во МАИ, 1992. -264с.
11. Поспелов Д.А. Логические методы анализа и синтеза схем. М.: Энергия, 1974.-228 с.
12. Рояк М.Э., Рояк С.Х. Математическая логика (метод. указания, часть 1). Новосибирск: Изд-во НГТУ, 1998. -61с.
13. Судоплатов С.В., Овчинникова Е.В. Дискретная математика: Учебник. –М.: ИНФРА-М; Новосибирск: Изд-во НГТУ, 2005. -256с.
14. Тихомирова Л.С. Методы минимизации булевых функций (методическая разработка). – Устинов: Изд-во УМИ, 1985. -36с.
15. Яблонский С.В. Введение в дискретную математику. –М.: Высш. шк., 2003. -384с.
16. Яблонский С.В., Гаврилов Г.П., Кудрявцев В.Б. Функции алгебры логики и классы Поста. –М.: Наука, 1966. -119с.
ПРИЛОЖЕНИЕ.
Задачи к практическим занятиям, выполнению расчетно-графических работ и для самостоятельного изучения методов минимизации ФАЛ.
№1. Записать формулу функции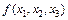 
и минимизировать ее геометрическим методом, методом карт Карно, Квайна, Квайна-Мак-Класки, неопределенных коэффициентов, минимизирующих карт. Сравнить результаты.
№2. Записать формулу функции 
и минимизировать ее методами Квайна, Квайна-Мак-Класки и карт Карно. Сравнить результаты.
№3. Записать формулу функции 
и минимизировать методом карт Карно.
№4. Во всех случаях заданий по п. №1,2,3 получить абсолютно минимальное представление ФАЛ в базисе {-,&,Ú}. Сравнить результаты.
№5. Записать исходную ФАЛ во всех случаях заданий по п. №1,2,3 в базисах Вебба и Шеффера методами неопределенных коэфициентов, минимизирующих, карт Квайна, Квайна-Мак-Класки, карт Карно. Сравнить резульаты.
Примечание
В таблицах по горизонтали стоят номера функций соответственно
варианту задания.
Задание №1: Варианты представления ФАЛ 
| х1 | х2 | х3 | ||||||||||||||||||||||||
[*] Использованы материалы разработки [14]
[†] Использованы материалы из книги [11].
