Образец отчета о выполнении работы 1.1
Принадлежности: Дозиметр ДБГ-06Т.
Проверим правильность работы ДБГ-06Т.
Данные измерений мощности экспозиционной дозы излучения, ni мкР/ч:
Таблица 1.
| № опыта | ||||||||||
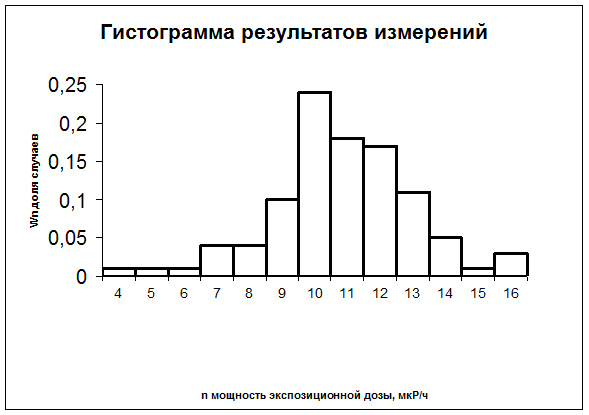
3. Представим результаты опыта в виде, удобном для построения гистограммы
(таблица 2). Построим гистограмму Wn=f(n):
Таблица 2
| Значение мощности (ni) экспозиционной дозы (мкР/ч) | |||||||||||||
| Число случаев наблюдений | |||||||||||||
| Доля случаев Wn | 0.01 | 0.01 | 0.01 | 0.04 | 0.04 | 0.1 | 0.24 | 0.18 | 0.17 | 0.11 | 0.05 | 0.01 | 0.03 |
|
|
|

4. Представим результаты опыта в таблице в удобном для промежуточных расчетов виде (таблица 3) и используя формулу (1), определим среднее значение мощности экспозиционной дозы излучения:
Таблица 3
| Значение мощности (ni) экспозиционной дозы (мкР/ч) | Число случаев наблюдений | Доля случаев наблюдений | å ni |
D ni = ni - 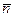 (мкР/ч)
(мкР/ч)
|
(D ni)2=
(ni - 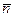 )2 )2
|
å
(ni - 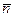 )2 )2
|
| 0,01 | -6,83 | 46,65 | 46,65 | |||
| 0,01 | -5,83 | 33,99 | 33,99 | |||
| 0,01 | -4,83 | 22,33 | 22,33 | |||
| 0,04 | -3,83 | 14,67 | 58,68 | |||
| 0,04 | -2,83 | 8,01 | 32,04 | |||
| 0,1 | -1,83 | 3,35 | 33,49 | |||
| 0,24 | -0,83 | 0,69 | 16,53 | |||
| 0,18 | 0,17 | 0,03 | 0,52 | |||
| 0,17 | 1,17 | 1,37 | 23,27 | |||
| 0,11 | 2,17 | 4,71 | 51,80 | |||
| 0,05 | 3,17 | 10,05 | 50,24 | |||
| 0,01 | 4,17 | 17,39 | 17,39 | |||
| 0,03 | 5,17 | 26,73 | 80,19 | |||
| å1083 | å467,12 |
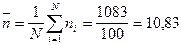 мкР/ч
мкР/ч
5. Найдем стандартную (среднеквадратичную) ошибку отдельного измерения используя таблицу 3 и формулу (2),:
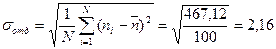 » 2 мкР/ч
» 2 мкР/ч
Округлим результат расчета, т.к. первая значащая цифра 2, то округлим до одной значащей цифры.
6. Отметим на гистограмме среднее значение мощности экспозиционной дозы 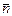 , округленное с учетом среднеквадратичной ошибки, а также значения
, округленное с учетом среднеквадратичной ошибки, а также значения  :
:
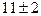 мкР/ч
мкР/ч
7.Измерим на гистограмме полуширину распределения, т.е. половину ширины гистограммы на уровне половины высоты. Сравним полученное значение с величиной 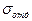 .
.
Половина высоты: 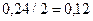
Полуширина распределения (13-10)/2 = 3/2 = 1,5 мкР/ч
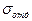 = 2 мкР/ч
= 2 мкР/ч
Сравним эти величины в процентном соотношении 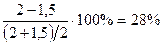 .
.
Вывод: величины различаются на 28%. Поскольку точность используемой методики оценки погрешностей составляет 20-30%, то эти величины можно считать равными, и вместо громоздких вычислений 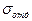 можно просто измерять полуширину гистограммы.
можно просто измерять полуширину гистограммы.
8. Определим долю случаев, когда отклонения от среднего значения 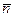 превышают
превышают 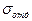 , 2
, 2 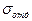 и сравним с теоретическими оценками:
и сравним с теоретическими оценками:
| Ошибка | Число случаев | Доля случаев | Теоретическая оценка |
± 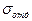 = ± 2 = ± 2
| 11+9=20 | 0,20 | 1-0,68=0,32 |
± 2 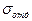 = ± 4 = ± 4
| 3+3=6 | 0,06 | 1-0,95=0,05 |
9. Определим стандартное отклонение величины 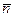 , используя всю совокупность измерений по формуле (3):
, используя всю совокупность измерений по формуле (3): 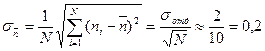 мкР/ч
мкР/ч
10. Найдем относительную ошибку этого результата по первому равенству (4):
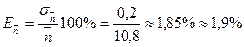
11. Окончательный результат, с учетом округления среднего значения в соответствии со стандартной ошибкой серии измерений:
n = (10,8 ± 0,2) мкР/ч.
Вывод: истинный результат измерения мощности экспозиционной дозы излучения с вероятностью 68 % находится с диапазоне 10,6¸11,0 мкР/ч.
Образец отчета о выполнении работы 1.2
Принадлежности: штангенциркуль, образец твердого тела.
1. Проведем измерения линейных размеров параллелепипеда (a - длина, b - ширина, с - высота). Измерения проведем по пять раз вдоль каждой из сторон через равные интервалы. Данные измерений представим в удобном для расчетов виде.
Таблица 1.1.
| № опыта | a, мм | 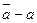 , мм , мм
| 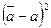 , мм2 , мм2
|
| 1. | 19,6 | -0,1 | 0,01 |
| 2. | 19,8 | 0,1 | 0,01 |
| 3. | 19,8 | 0,1 | 0,01 |
| 4. | 19,8 | 0,1 | 0,01 |
| 5. | 19,5 | -0,2 | 0,04 |
| å | 98,5 | 0,0 | 0,08 |
| Среднее значение | 19,70 | - | - |
| Случайная погрешность измерений | 0,06 | ||
| Систематическая погрешность (инструментальная) | 0,05 | ||
| Полная погрешность | 0,08 |
Таблица 1.2.
| № опыта | b, мм | 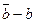 , мм , мм
| 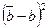 , мм2 , мм2
|
| 1. | 70,0 | 0,02 | 0,0004 |
| 2. | 69,9 | 0,12 | 0,0144 |
| 3. | 70,1 | -0,08 | 0,0064 |
| 4. | 70,0 | 0,02 | 0,0004 |
| 5. | 70,1 | -0,08 | 0,0064 |
| å | 350,1 | 0,0 | 0,028 |
| Среднее значение | 70,02 | - | - |
| Случайная погрешность измерений | 0,03 | ||
| Систематическая погрешность (инструментальная) | 0,05 | ||
| Полная погрешность | 0,06 |
Таблица 1.3.
| № опыта | с, мм | 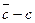 , мм , мм
| 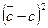 , мм2 , мм2
|
| 1. | 29,5 | 0,26 | 0,0676 |
| 2. | 29,8 | -0,04 | 0,0016 |
| 3. | 29,9 | -0,14 | 0,0196 |
| 4. | 29,9 | -0,14 | 0,0196 |
| 5. | 29,7 | 0,06 | 0,0036 |
| å | 148,8 | 0,0 | 0,112 |
| Среднее значение | 29,76 | ||
| Случайная погрешность измерений | 0,07 | ||
| Систематическая погрешность (инструментальная) | 0,05 | ||
| Полная погрешность | 0,09 |
2. Пользуясь формулами (1) и (3) из первой части лабораторной работы рассчитаем погрешности прямых измерений и данные занесем в таблицы 1:
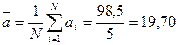 (мм)
(мм)
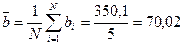 (мм)
(мм)
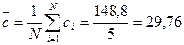 (мм)
(мм)
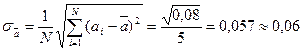 (мм)
(мм)
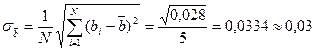 (мм)
(мм)
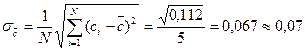 (мм)
(мм)
3. Систематическая погрешность измерений всех величин равна половине цены деления штангенциркуля, т.е. 0,05 мм. Занесем данные в таблицу.
4. Произведем расчет полной погрешности измерений параметров а, в и с по формуле (11) методических указаний к лабораторной работе, предварительно оценив величины случайной и систематической погрешностей. 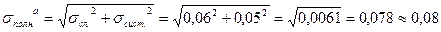 (мм)
(мм)
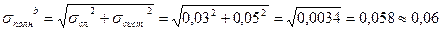 (мм)
(мм)
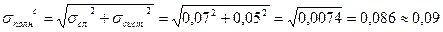 (мм)
(мм)
Если для измерения величин а, b или с систематическая погрешность более чем в два раза превышает случайную (или наоборот случайная больше) тогда ее вклад в полную погрешность менее 20 %, и при вычислениях случайной погрешностью можно пренебречь (или наоборот), в качестве полной погрешности а взять систематическую погрешность (или наоборот случайную т.е. большую). Данные занесем в таблицу.
5. Вычислим V образца. Т.к. 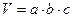 воспользуемся формулой (9), следовательно:
воспользуемся формулой (9), следовательно:
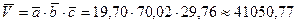 (мм 3)
(мм 3)
Ожидаемую погрешность рассчитаем по формуле (10):
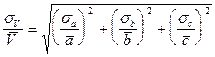
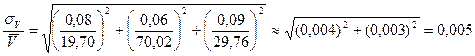
Поскольку 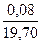 и
и 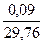 примерно равны, и они отличаются более чем в 2 раза от
примерно равны, и они отличаются более чем в 2 раза от 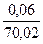 мы можем пренебречь меньшей величиной при расчете и можем проводить вычисления ограничившись двумя слагаемыми под знаком корня. Т.о. погрешность измерения объема:
мы можем пренебречь меньшей величиной при расчете и можем проводить вычисления ограничившись двумя слагаемыми под знаком корня. Т.о. погрешность измерения объема:
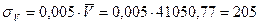 (мм 3)
(мм 3)
Т.о. окончательный результат измерений объема с учетом округления результата:
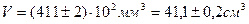
6. Вычислим плотность материала, из которого изготовлен образец. Массу образца возьмем в таблице т = 232,10 ± 0,05 г. Погрешность табличной величины всегда равна половине минимального действующего разряда в записи этой величины:
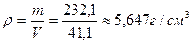
Оценим погрешность:
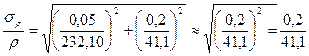
При оценке погрешности вычисления плотности действуем, как и в ранее рассмотренном случае, пренебрегаем относительной погрешностью значения массы и округляем результат.
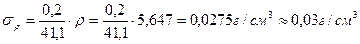
Окончательный ответ:
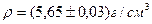





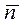
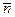 σотд σотд
σотд σотд