Определение отношения электрона

ЛАБОРАТОРНАЯ РАБОТА N 220.

ТЕОРИЯ

Закон Ампера. Характеристика магнитного поля, единицы их измерения.

Движущиеся заряды /токи/ изменяют свойства окружающего их пространства - создают в них магнитное поле. Его наличие проявляется в том, что на движущиеся в нем заряды /токи/ действуют силы, т.е. взаимодействие токов осуществляется через магнитное поле. Закон взаимодействия токов был установлен в 1820 году Ампером. Он пришел к выводу, что сила F, которая действует на прямолинейный проводник с током, находящийся в однородном магнитном поле, прямо пропорциональна силе тока I в проводнике, его длине l, магнитной индукции поля В и синусу угла 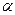между направлением тока в проводнике и вектором В;

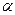F = I · В · ·sin (1)

Закон Ампера можно применять также для неоднородного магнитного поля и проводника произвольной формы. Бесконечно малый элемент d проводника любой формы можно считать прямолинейным, а магнитное поле в области, занятой элементом d , можно считать однородным. Поэтому в общем случае закон Ампера имеет следующий вид:

d F =I · В· d · sin(d , B), (2)

где d F - сила, действующая на элемент проводника длиной d ;

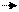
угол 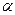заменен углом между векторами d (вектор, равный повеличине d и имеющий направление тока) и вектором В. Закон Ампера можно записать и в векторной форме:

d F = I [ d ·В] (3)

Отсюда следует, что вектор силы d F направлен перпендикулярно к плоскости, образованной векторами d и В таким образом, чтобы из конца вектора d F вращение от вектора d к вектору В по кратчайшему пути происходило против часовой стрелки, (рис.1).

Направление силы, действующей на проводник с током, удобно определять с помощью так называемого правила левой руки. Если рассмотреть левую руку, расположенную так, чтобы вектор В "вонзился" в ладонь, а четыре пальца были направлены вдоль тока, то отставленный в сторону большой палец укажет направление силы (рис.2). Закон Ампера позволяет оп­ределить численное значение силовой характеристики магнитного поля вектора магнитной индукции В.

 

d

Рис.1. Сила Ампера

Предположим, что элемент проводника d с током I перпендикулярен направлению магнитного поля, т.е. sin (d ,В) = 1. Тогда, в соответствии с законом Ампера, можно записать величину магнитной индукции в виде:

 

В = (4)

 

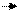Рис.2. Правило левой руки.

Из этой формулы следует, что магнитная индукция В численно равна силе, действующей со стороны магнитного поля на единицу длины проводника, по которому течет ток единичной силы и который расположен перпендикулярно к направлению магнитного поля. В СИ за единицу магнитной индукции, называемой тесла (Т), принимается магнитная индукция такого магнитного поля, которое действует с силой в I Ньютон на каждый метр длины прямолинейного проводника, расположенного перпендикулярно к направлению поля, если по этому проводнику проходит ток в I ампер.

Из формулы (4) следует, что

I T=I

В абсолютной электромагнитной системе единиц (СГСМ) единица измерения магнитной индукции называется гауссом: (Гс):1Гс = 10^-4 Т.

Наряду с магнитной индукцией В магнитное поле характеризуется и другой величиной - вектором напряженности Н, который связан с вектором В следующим отношением:

Н= (5)

где - относительная магнитная проницаемость среды (величина безразмерная), - магнитная постоянная, равная 4 10^-7 . Если В - вектор магнитной индукции поля тока в среде, а В₀ -вектор магнитной индукции поля тока в вакууме, то

= (6)

В СИ за единицу измерения напряженности магнитного поля, называемую ампер на метр (А/м), принимается напряженность такого поля, магнитная индукция которого равна в вакууме 4 10^-7 Т.

В СГСМ напряженность магнитного поля измеряется в эрстедах (Э)

IЭ=10³/4 А/м 80А/м

Сила Лоренца. Сила Ампера, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные, движущиеся заряды, а уже от этих зарядов действие передается проводнику, по которому они перемещаются. На отдельный заряд q, 'движущийся со скоростью V в магнитном поле с индукцией В, действует сила, называемая силой Лоренца.

F_л=q[VB] (7)

Особенностью силы Лоренца является ее зависимость от скорости частицы и знака заряда (рис.3). Эта сила перпендикулярна векторам V и В и вызывает лишь изменение траектории заряженной частицы. Часто лоренцевой силой называют сумму электрической и магнитной сил, действующих на заряд в электромагнитном поле:

F_л=qЕ+ q[VB]

здесь Е - вектор напряженности электрического поля.

 

Рис.3. Сила Лоренца

Действием силы Лоренца объяс­няется эффект Холла, заключа­ющийся в появлении поперечной разности потенциалов в образ­це с током, помещенным в маг­нитное поле. Закон Био - Савара - Лапласа позволяет определить вектор магнитной индукции в каждой точке поля, которое создается током, текущим по проводнику любой формы. Закон записывается в следующем виде:

 

dB= [d ,r] (9)

 

или

 

dB= sin(d ,r) (10)

где d ,- элемент проводника с током; г радиус вектор, проведенный из элемента проводника d в рассматриваемую точку поля С; r - модуль радиуса-вектора r (рис.4). Из формулы (9) следует, что вектор магнитной индукции в какой-либо точке С магнитного поля направлен перпендикулярно к плоскости, в которой лежат векторы d и r таким образом, что из конца вектора dB поворот вектора d до совмещения с вектором r по кратчайшему пути виден происходящим против часовой стрелки. Вектор магнитной индукции В в каждой точке поля любого проводника с током представляет собой векторную сумму индукций dВ элементарных магнитных полей, создаваемых каждым участком d этого проводника, ибо при наложении магнитных полей справедлив принцип суперпозиции, т.е. принцип независимого наложения полей. Поэтому В =s d , где символ означает, что интегрирование распространено на всю длину проводника.

Расчет показывает, что индукция магнитного поля бесконечно длинного проводника с током I выражается формулой:

B= (11)

где а - кратчайшее расстояние от данной точки поля до проводника с током.

Рис.4. Магнитная индукция элемента проводника с током.

 

ЛАБОРАТОРНАЯ РАБОТА N220.

ОПРЕДЕЛЕНИЕ ОТНОШЕНИЯ ЭЛЕКТРОНА