Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное
Учреждение высшего профессионального образования
«Тульский государственный университет»
Кафедра математического анализа
К О Н Т Р О Л Ь Н О - К У Р С О В А Я Р А Б О Т А
Объектно-ориентированное программирование в среде Delphi.
Вариант № 1. Гамма-функция.
Выполнил: студент группы 520301 Алексеев В.Г.
Проверил: Кудряшов А.В.
ТУЛА 2012
Содержание
Описание работы и структуры программы 3
1 Описание используемых объектов 3
2 Описание используемых подпрограмм 4
Текст программы 6
Контрольные примеры работы программы 10
Описание работы и структуры программы
1 Описание используемых объектов
1. form1 – основная форма
a. cht1 – поле графика гамма-функции
b. edt1 – поле для ввода начального значения гамма-функции
c. edt2 – поле для ввода конечного значения гамма-функции
d. lbl1 – подпись для edt1
e. lbl2 – подпись для edt2
f. lbl4 – поле для сообщения о недопустимых значений в edt1
g. lbl5 – поле для сообщения о недопустимых значений в edt2
h. mm1 – меню
i. {N2} – кнопка запуска построения графика
ii. {N1} – кнопка вызова окна настройки
2. form2 -вспомогательная форма
a. edt1 – поле для ввода количества точек для графика функции
b. lbl1 – подпись
c. btn1 – кнопка сохранения введенного значения
2 Описание используемых подпрограмм
1. function Fact(n:integer):extended; -подпрограмма определения значения факториала числа n;
В функции реализован рекурсивный алгоритм определения факториала, основанный на формуле:
Критерием остановки рекурсивной процедуры служит условие
2. function Power(x:real;n:integer):extended; -подпрограмма определения целой степени числа. Здесь x – основание степени, n – показатель степени;
В функции реализован рекурсивный алгоритм определения целой степени числа, основанный на формуле:
Критерием остановки рекурсивной процедуры служит условие
3. function gam(z:Extended):Extended;- подпрограмма определения значения гамма-функции на основании формул 
, 
,
|
Параметры функции: z – аргумент функции, массивы TA,TB – коэффициенты полиномов аппроксимации, k – степень полиномов, x – коэффициент для расчета полиномов, z1 – произведение выносимых значений для формулы .
В подпрограмме реализован расчет значений гамма-функции на отрезке (1,2). В цикле рассчитываются значения полиномов. Далее в цикле рассчитываются значения гамма-функции для z>2 по формуле . После чего вычисляется значение исходной функции по формуле.
4. function gamzer(z:Extended):Extended; -подпрограмма определения значения гамма-функции на отрезке (0,1) на основании формулы . Параметры функции: z – аргумент функции.
Значение гамма-функции вычисляется по формуле .
procedure TForm1.edt3KeyPress, procedure TForm1.edt2KeyPress
Процедура запрещает ввод в полях edt3, edt2 символов, не являющихся числами.
6. procedure TForm1.N2Click(Sender: TObject);
Запуск программы с введенными значениями.
7. procedure TForm1.N1Click(Sender: TObject);
Вывод окна настройки количества точек.
Основная программа проверяет значения, введенные в полях edt2, edt3. В случае, если данные введены некорректно, то выдается сообщение об ошибке. Если данные не введены, программа выполняется для стандартных значений. Если введенные данные корректны, происходит вывод графика значений гамма-функции для выбранного количества точек на отрезке.
Координата левой границы 
-го отрезка определяется из выражения:
, 
Для каждой точки 
определяются значения гамма-функции в зависимости от значений c с помощью условных операторов. Для значений на отрезке (0,1) выполняется функция gamzer, для целых значений c>1 выполняется функция fact(c-1), в остальных случаях выполняется gam.
2 Текст программы
unit gamma;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, ExtCtrls, TeeProcs, TeEngine, Chart, Series, Menus, Unit2;
type
TForm1 = class(TForm)
lbl1: TLabel;
lbl2: TLabel;
edt1: TEdit;
edt2: TEdit;
lbl4: TLabel;
lbl5: TLabel;
lbl6: TLabel;
cht1: TChart;
lnsrsSeries1: TLineSeries;
mm1: TMainMenu;
N1: TMenuItem;
N2: TMenuItem;
procedure edt3KeyPress(Sender: TObject; var Key: Char);
procedure edt2KeyPress(Sender: TObject; var Key: Char);
procedure N2Click(Sender: TObject);
procedure N1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
function Power(x:real;n:integer):extended;
function fact(z:extended):extended;
function gam(z:Extended):Extended;
function gamzer(z:Extended):Extended;
var
Form1: TForm1;
a1,a2,c,h,f,er,rez,z:extended;
N,nl:integer;
correct:Boolean;
implementation
{$R *.dfm}
function Power(x:real;n:integer):extended; // функция возведения в степень
begin
if n=0 then Power:=1
else Power:=x*Power(x,n-1);
end;
function fact(z:extended):extended; //факториал
begin
if z<=0 then Fact:=1
else Fact:=z*Fact(z-1);
end;
function gam(z:Extended):Extended; // вычисление гамма-функции при z>1
type TA=array[1..8] of Extended;
type TB=array[1..8] of Extended;
var A:TA;
var B:TB;
const E=2.7182818284;
var k:Integer;
var x:Extended;
var P08,P18:Extended;
var z1:Extended;
begin
A[1]:=6.64561438202405440627855e+4;
a[2]:=-3.61444134186911729807069e+4;
a[3]:=-3.14512729688483675254357e+4;
a[4]:=8.66966202790413211295064e+2;
a[5]:=6.29331155312818442661052e+2;
a[6]:=-3.79804256470945635097577e+2;
a[7]:=2.47656508055759199108314e+1;
a[8]:=-1.71618513886549492533811e+0;
b[1]:=-1.15132259675553483497211e+5;
b[2]:=-1.34659959864969306392456e+5;
b[3]:=4.75584627752788110767815e+3;
b[4]:=2.25381184209801510330112e+4;
b[5]:=-3.10777167157231109440444e+3;
b[6]:=-1.01515636749021914166146e+3;
b[7]:=3.15350626979604161529144e+2;
b[8]:=-3.08402300119738975254353e+1;
x:=z-1;
z1:=1;
P08:=0;
P18:=power(x,8);
for k:=1 to 8 do
begin
P08:=P08+a[k]*power(x,k);
P18:=P18+b[k]*power(x,k-1);
end;
while z>2 do
begin
z1:=z1*(z-1);
z:=z-1;
end;
if (z>1) and (z<2) then
begin
gam:=z1*(1+P08/P18);
end;
end;
function gamzer(z:Extended):Extended; //вычисление гамма-функции на отрезке (0,1)
begin
gamzer:=gam(z+1)/z;
end;
procedure TForm1.edt3KeyPress(Sender: TObject; var Key: Char);
begin
if not ((Key='1') or (Key='2') or (Key='3') or (Key='4') or (Key='5') or (Key='6') or (Key='7') or (Key='8') or (Key='9') or (Key='0') or (Key=#8)) then Key:=#0;
end;
procedure TForm1.edt2KeyPress(Sender: TObject; var Key: Char);
begin
if not ((Key='1') or (Key='2') or (Key='3') or (Key='4') or (Key='5') or (Key='6') or (Key='7') or (Key='8') or (Key='9') or (Key='0') or (Key=#8) or (key=',')) then Key:=#0;
end;
procedure TForm1.N2Click(Sender: TObject);
begin
Form1.lbl4.Caption:='';
Form1.lbl5.Caption:='';
Form1.lbl6.Caption:='';
if (Form1.edt1.Text='') then Form1.edt1.Text:='0,1';
if (Form1.edt2.Text='') then Form1.edt2.Text:='1';
a1:=StrToFloat(Form1.edt1.text);
a2:=StrToFloat(Form1.edt2.text);
N:=StrToInt(Form2.edt1.text);
er:=frac(N);
correct:=True;
Form1.cht1.Series[0].Clear;
if (a1<=0) or (a1>10) then
begin
Form1.lbl4.caption:='Некорректные значения';
correct:=False;
end;
if (a2<=0) or (a2>10) then
begin
Form1.lbl5.caption:='Некорректные значения';
correct:=False;
end;
if a2<=a1 then
begin
Form1.lbl5.Caption:='Некорректные значения';
correct:=False;
end;
if correct then
begin
c:=a1;
h:=abs(a1-a2)/N;
f:=frac(c);
end;
if correct then
begin
while c<=a2 do //вычисление гамма-функции в зависимостиот исходных параметров
begin
if (c>0) and (c<1) then
begin
rez:=gamzer(c);
end;
if c=1 then rez:=1;
if (c>1) then
begin
if f=0 then rez:=fact(c-1)
else rez:=gam(c);
end;
Form1.cht1.Series[0].AddXY(c,rez);
c:=c+h;
f:=frac(c);
end;
end;
end;
procedure TForm1.N1Click(Sender: TObject);
begin
Form2.Show;
end;
end.
3 Контрольные примеры работы программы.
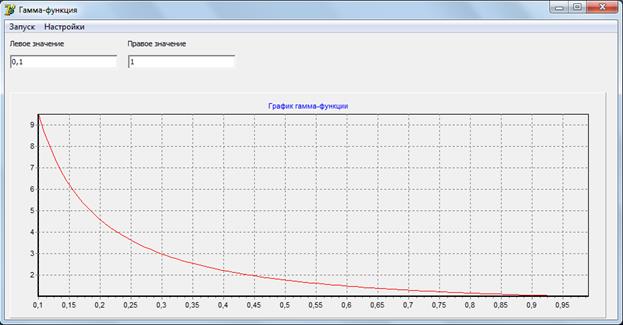
Пример выполнения программы с настройками по умолчанию.
Окно настроек программы.
Вид графика функции с новыми настройками.
