Проведение опыта и обработка результатов

 

1. Замерить размеры тарировочной балки b₀, h₀, ℓ.

2. Увеличивая нагрузку на ∆Р = 1 кг, определить показа­ния прибора для всех датчиков при каждой нагрузке.

3. Вычислить среднее приращение показаний для каждого датчика.

 

 

 

Точку приложения силы называют полюсом.

Нормальные напряжения в произвольной точке исследуемого сечения определяют по формуле:

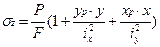. (19)

где Р - растягивающая сила;

F - площадь поперечного сечения;

i_x, i_y - радиусы инерции сечения;

x_p, y_p - координаты полюса;

x, y - координаты произвольной точки.

Если растягивающая сила лежит в одной из главных плоскостей инерции, то такой; случай внецентренного растяжения называется плоским.

 

 

Рис. 14 Схема плоского внецентренного растяжения.

 

Формула для вычисления напряжений при плоском внецентренном растяжении:

.

 

 

 

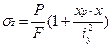ЛАБОРАТОРНАЯ РАБОТА № 12

ОПЫТНАЯ ПРОВЕРКА ТЕОРИИ ВНЕЦЕНТРЕННОГО РАСТЯЖЕНИЯ.

 

Цель работы - определить опытным путем напряжения в несколь­ких точках внецентренно растянутого стержня и сравнить опыт­ные данные с расчетными величинами.

 

Основные понятия

Внецентренным растяжением /сжатием/ называют такой вид нагружения стержня, когда растягивающая /или сжимающая/ сила направлена параллельно оси стержня на некотором расстоянии от нее.

Внецентренное растяжение можно представить как совокупность осевого растяжения и изгиба в двух плоскостях /рис. 13/.

 

Рис. 13 Внецентренное растяжение стержня.

 

 

 

 

4. Подсчитать среднее по абсолютной величине приращение
показаний для всех датчиков. При этом разность приращений для третьего и пятого датчиков предварительно увеличить в 3-4 раза.

5. Определить цену деления прибора;

а/ в относительных деформациях

, (13)

приняв модуль упругости Е=2*10⁶ МН/м²;

 

б/ в напряжениях

. (14)

 

 

ЛАБОРАТОРНАЯ РАБОТА № 10

ОПЫТНАЯ ПРОВЕРКА ТЕОРИИ ПЛОСКОГО ИЗГИБА

 

Цель работы - экспериментально проверить расчетную формулу нормальных напряжений в поперечном сечении при изгибе балки.

Основные понятия.

Нормальные напряжения при изгибе пря­мого бруса

вычисляют по формуле:

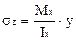, (15)

где М_х - изгибающий момент в данном поперечном сечении;

I_x - момент инерции сечения относительно нейтральной

оси;

у - расстояние от нейтральной оси до точки, в которой определяется напряжение.

Из формулы следует, что нормальные напряжения линейно меняются по высоте сечения, они равны нулю на центральной оси и достигают максимальной величины в слоях наиболее удаленных от нее.

 

 

 

 

Формула справедлива для напряжений, не превышающих предел пропорциональности материала, то есть для таких нагрузок, кото­рый вызывают только упругие деформации.

При выводе расчетной формулы предполагалось, что в направ­лениях, параллельных оси балки, материал испытывает только растяжение или сжатие.

Это допущение позволяет находить величины напряжений в различных точках поперечного сечения балки, измеряя величины деформаций ε и пользуясь формулой закона Гука

,

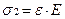где Е - модуль упругости материала балки.

 

Постановка опыта.

Для испытания на изгиб используется балка, опирающаяся по концам на шарнирные опоры. /рис. 9/.

 

 

 

Рис. 9 Схема балки и расположения на ней

тензодатчиков.

 

Исследуем сечение m-m.

 

 

 

3. Нагружать брус последовательно возрастающими силами с равной величиной приращения нагрузки ∆Р = 1т, снимать показания всех датчиков и заносить в таблицу результатов измерений.

4. Найти средние приращения показаний ∆n_ср для каждого
датчика,

5. Вычислить опытные приращения нормальных напряжений для каждой точки

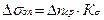
(К_σ - цена деления прибора).

6. Вычислить теоретические значения напряжений в тех же
точках по формуле (17), используя таблицу расчета, приведенную в лабораторном журнале.

7. По найденным опытным величинам построить эпюру распределения нормальных напряжений в сечении кривого брусa и сравнить ее с эпюрой, полученной по данным теоретического расчета /рис. 12/

 

Рис. 12 Эпюры нормальных напряжений.

 

 

 

 

 

Рис. II

Геометрические пара­метры сечения кривого

бруса.

Постановка опыта.

Для испытания используется кривой брус круглого очертания с прямоугольным поперечным сечением.

Тензодатчики наклеены в девяти точках боковой поверхнос­ти его опасного сечения n-n /рис. 10/. Датчики подклю­чают к тензометру ВСТ-3 или цифровому измерителю деформаций ИДЦ-1.

Нагружение бруса растягивающими силами Р производится на машине Р-50 или УММ-10. При этом внутренние волокна бруса растягиваются, а наружные сжимаются. Вместе с волокнами изменя­ется длина проволоки тензодатчиков и их электросопротивление, что и фиксируется приборами.