2. 1. ДИФФЕРЕНЦИРУЮЩАЯ RC -ЦЕПЬ
Цепь, состоящая из последовательно включенных конденсатора емкостью С и резистора с сопротивлением R, называется RC -цепью. Одной из основных характеристик RC -цепи является величина t = RC, имеющая размерность времени.
|
 |
Рассмотрим схему, изображенную на рис. 2.1. Здесь U 1 – входное напряжение, а выходное напряжение U 2 снимается с резистора. При этом мы считаем, что прибор, которым измеряется выходное напряжение, имеет бесконечно большое входное сопротивление и ток через него не идет.
По второму правилу Кирхгофа
где I – входной ток.
Дифференцируя по времени (при R = const), получаем
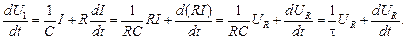
Таким образом, приходим к выражению
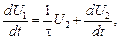
т. к. выходное напряжение U 2 в данном случае равно напряжению на сопротивлении UR.
При τ → ¥: 
<< 
, 
, т.е. U 1 ≈ U 2. Это приближение реализуется в случае быстрых сигналов (
>> 
), для которых τ >> 1/ω, или, иначе, τ >> Т (ω– циклическая частота сигнала, Т – период). В этом случае цепь используется для передачи изменений сигнала без передачи постоянной составляющей.
При τ → 0: << и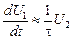 
, т.е. 
. Следовательно, при малых τ такая RC-цепь осуществляет дифференцирование входного сигнала. Это приближение реализуется в случае медленных сигналов ( << ), для которых τ << 1/ω или τ << Т.
Для гармонической ЭДС аналогичный результат легко получить, вычисляя коэффициент передачи цепи по напряжению который определяется следующим образом:
где φ = φ2 – φ1.
Коэффициент передачи цепи показывает, какая часть входного напряжения передается на выход цепи. При этом модуль |γ| и аргумент φ = φ2 – φ1 (равный фазовому сдвигу между напряжениями на выходе и входе) являются вещественными функциями частоты. Зависимость модуля коэффициента передачи от частоты называется амплитудно-частотной характеристикой (АЧХ) цепи, а зависимость аргумента коэффициента передачи от частоты – фазочастотной характеристикой (ФЧХ).
Так как в нашем случае импеданс цепи Z = XC + R, то для входного напряжения получим
Выходное напряжение, как уже упоминалось, U 2 = IR. Следовательно
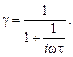
При τ << 1/ω (случай медленных сигналов) γ ≈ iωτ. При этом сдвиг фаз между входным и выходным напряжениями (аргумент γ) равен π/2, что эквивалентно дифференцированию.
При τ >> 1/ω (случай быстрых сигналов) γ ≈ 1, т. е. сигнал проходит без искажений.
В общем случае модуль и аргумент коэффициента передачи будут равны соответственно:
При достаточно больших частотах, когда ω >> 1/τ и ω → ∞, 
→ 0, тогда |γ| → 1.
При малых частотах, когда ω << 1/ τ и ω → 0, >> 1, тогда |γ| → 0.
Эта зависимость показана на рис. 2.2. Представленная на этом рисунке зависимость характерна для фильтров высоких частот, которые пропускают высокие частоты и не пропускает низкие.
 |
2. 2. ИНТЕГРИРУЮЩАЯ RC -ЦЕПЬ
|
 |
Рассмотрим случай, когда выходным звеном RC -цепи является конденсатор (рис. 2.3). Тогда аналогично первому случаю:
U 1 = IR + UC, 
Из последнего равенства получаем:
откуда 
Поскольку в данном случае U 2 = UC, то приходим к выражению:
При τ → 0 (для медленных сигналов) U 2 ≈ U 1. Такие сигналы цепь пропускает без искажений.
При τ → ∞ (быстрые сигналы):
или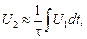 
т. е. происходит интегрирование входного сигнала. Поэтому данная цепь называется интегрирующей.
Коэффициент передачи интегрирующей цепи равен:
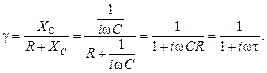
При ω << 1/τ (медленные сигналы) γ ≈ 1. При ω >> 1/τ (быстрые сигналы) 
и аргумент γ равен –π/2, что соответствует интегрированию.
В общем случае выражения для модуля и аргумента коэффициента передачи интегрирующей цепи имеют следующий вид:
φ = – arctg (ωτ).
При достаточно больших частотах, когда ω >> 1/τ и ω → ∞, ω2τ2 >> 1, |γ| → 
, |γ| → 0.
При малых частотах, когда ω << 1/τ и ω → 0, тогда |γ| → 1.
Эта зависимость качественно показана на рис. 2.4. Представленная на этом рисунке зависимость характерна для фильтров низких частот, которые пропускают низкие частоты и не пропускает высокие.
 |
ЛАБОРАТОРНЫЕ РАБОТЫ
Лабораторная работа № 3
Исследование высокочастотного фильтра. Дифференцирующая RC -цепь.
1. Построить схему дифференцирующей RC -цепи, используя программу моделирования электрофизических процессов Electronics WorkBench, как показано на рисунке 1. К входу и выходу цепи подключить осциллограф и АЧХ-метр.
2. Для значений R и C, заданных преподавателем, рассчитать постоянную времени τ. Исследовать моделированием зависимости | Z | - модуля импеданса (полного сопротивления) цепи, |γ| - модуля коэффициента передачи, φ - аргумента коэффициента передачи от частоты с помощью осциллографа и АЧХ-метра. Построить графики перечисленных зависимостей. Построить векторную диаграмму RC -цепи.
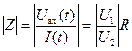, где (U вх = U 1 ,U вых = U 2),
,
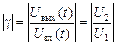arg (γ) = φ (U вых) – φ (U вх) =φ (U 2) – φ (U 1) = – arg(Z),
arg (Z) = φ (U вх) – φ (I вых) = φ (U 1) – φ (U 2).
3. Как изменится АЧХ цепи при увеличении τ = RC в два раза (или увеличиваем R в два раза, или увеличиваем C в два раза, или увеличиваем R и C: 2τ = (2 R) C = R (2 C) = (
R) ( C). Проанализировать форму выходного сигнала для различных значений R и C. Результаты анализа занести в табл. 1.
Таблица 1
| R | C | τ | вид входного и выходного сигнала |
4. Проанализировать форму выходного сигнала при различных частотах входных сигналов прямоугольной формы с заполняемостью 50%. Результаты занести в таблицу 2.
Таблица 2
| f | вид входного и выходного сигнала |
5. Собрать и зарисовать схему дифференцирующей RC -цепи, используя реальные приборы. Повторить экспериментальную часть пункта 2.
Лабораторная работа № 4
Исследование низкочастотного фильтра. Интегрирующая RC -цепь
1. Построить схему интегрирующей RC -цепи, используя программу моделирования электрофизических процессов Electronics WorkBench, как показано на рисунке 2. К входу и выходу цепи подключить осциллограф и АЧХ-метр.
 | |||
|
2. Для значений R и C, заданных преподавателем, рассчитать постоянную времени τ. Исследовать моделированием зависимости модуля импеданса (полного сопротивления) цепи, модуля коэффициента передачи, аргумента коэффициента передачи от частоты с помощью осциллографа и АЧХ-метра. Построить графики перечисленных зависимостей. Построить векторную диаграмму.
3. Как изменится АЧХ цепи при увеличении τ в два раза. Проанализировать форму выходного сигнала для различных значений R и C. Результаты занести в таблицу 1 (см. лабораторную работу № 3).
4. Проанализировать форму выходного сигнала при различных частотах входных сигналов треугольной формы с заполняемостью 50 %. Результаты занести в таблицу 2 (см. лабораторную работу № 3).
5. Собрать и зарисовать схему интегрирующей RC -цепи, используя реальные приборы. Повторить экспериментальную часть пункта 2.
